单调栈笔记
发布时间:2024年01月23日
单调栈正如其名字,用一个栈(能够实现栈性质的数据结构就行)来存储元素,存储在栈中的元素保持单调性(单调递增或者是单调递减)。单调常用来解决寻找任一个元素左边或者右边第一个比自己小或者大的元素位置,大家可以想象看,如果是只需要找某一个元素的话,我们遍历一次数组就好了,但是如果是找数组中所有元素的左边或者右边第一个比自己小或者大的元素位置时,那么每找一次遍历一次数组的话,这样会是O(n^2)的时间复杂度,单调栈就是来实现一次遍历解决问题的办法。
具体如何实现,以及单调栈如何维护的,请看下面的题目
1.每日温度
 这个题目是单调栈的经典应用,我们需要找到下一个比当前天气温高的日子出现在几天之后。
这个题目是单调栈的经典应用,我们需要找到下一个比当前天气温高的日子出现在几天之后。
1.单调栈中存储的是数组下标index
2.单调栈中:栈顶到栈底保持单调递减
class Solution {
public:
vector<int> dailyTemperatures(vector<int>& temperatures) {
vector<int> ans(temperatures.size(), 0);
//定义一个单调栈
vector<int> stack;
for(int i = 0; i < temperatures.size(); i++){
if(stack.size() == 0 || temperatures[stack.back()] >= temperatures[i]){
stack.push_back(i);
}else{
//将单调栈中所有小于当前元素的栈针弹出来(保持单调性)
while(stack.size() > 0 && temperatures[stack.back()] < temperatures[i]){
int index = stack.back();
stack.pop_back();
ans[index] = i - index;
}
//将当前元素添加到栈中
stack.push_back(i);
}
}
return ans;
}
};
2.下一个更大元素 I

这个题目可以利用我们普通暴力解法(多层循环)实现,但是下面给出的是单调栈的实现
class Solution {
public:
vector<int> nextGreaterElement(vector<int>& nums1, vector<int>& nums2) {
vector<int> stack;//单调栈
unordered_map<int, int> m; //存储nums2中 nums2[i]和i的键值对
vector<int> first_max_index(nums2.size(), -1);
for(int i = 0; i < nums2.size(); i++){
//先将nums2[i]和i的键值对存储好
m[nums2[i]] = i;
//开始单调栈的过程
if(stack.empty() || nums2[stack.back()] >= nums2[i]){
stack.push_back(i);
}else{
while(!stack.empty() && nums2[stack.back()] < nums2[i]){
int index = stack.back();
stack.pop_back();
first_max_index[index] = i;
}
stack.push_back(i);
}
}
vector<int> ans(nums1.size(), -1);
for(int i = 0; i < nums1.size(); i++){
//nums1[i]在nums2中下标
int index = m[nums1[i]];
//获得nums2[index]右侧第一个大于的元素
int first_index = first_max_index[index];
if(first_index != -1) ans[i] = nums2[first_index];
}
return ans;
}
};
3.下一个更大的元素
 这个题目在上一个题目的基础上,将数组收尾相连了起来,而且数组长度也变大了,所以就不能够通过暴力求解了,只能够通过单调栈来实现。
这个题目在上一个题目的基础上,将数组收尾相连了起来,而且数组长度也变大了,所以就不能够通过暴力求解了,只能够通过单调栈来实现。
思路:直接在原数组再拼接一个原数组(解决首尾相连),然后通过单调栈来找下一个更大元素
class Solution {
public:
vector<int> nextGreaterElements(vector<int>& nums) {
int n = nums.size();
//将循环数组给铺平
for(int i = 0; i < n; i++){
nums.push_back(nums[i]);
}
vector<int> ans(n * 2, -1);
vector<int> stack;
for(int i = 0; i < 2 * n; i++){
if(stack.empty() || nums[stack.back()] >= nums[i]){
stack.push_back(i);
}else{
while(!stack.empty() && nums[stack.back()] < nums[i]){
int index = stack.back();
stack.pop_back();
ans[index] = nums[i];
}
stack.push_back(i);
}
}
for(int i = 0; i < n; i++){
ans.pop_back();
}
// 写法二:最后再把结果集即ans数组resize到原数组大小
//ans.resize(nums.size() / 2);
return ans;
}
};
方法优化,不通过拼接解决收尾相连
// 版本二
class Solution {
public:
vector<int> nextGreaterElements(vector<int>& nums) {
vector<int> result(nums.size(), -1);
if (nums.size() == 0) return result;
stack<int> st;
for (int i = 0; i < nums.size() * 2; i++) {
// 模拟遍历两边nums,注意一下都是用i % nums.size()来操作
while (!st.empty() && nums[i % nums.size()] > nums[st.top()]) {
result[st.top()] = nums[i % nums.size()];
st.pop();
}
st.push(i % nums.size());
}
return result;
}
};
4.接雨水

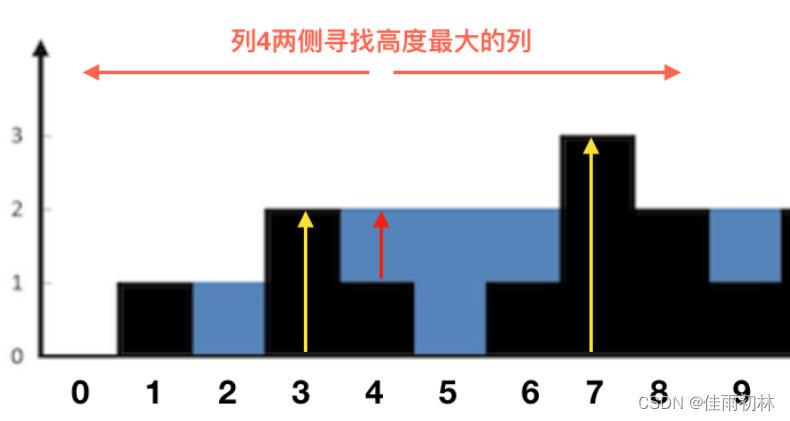
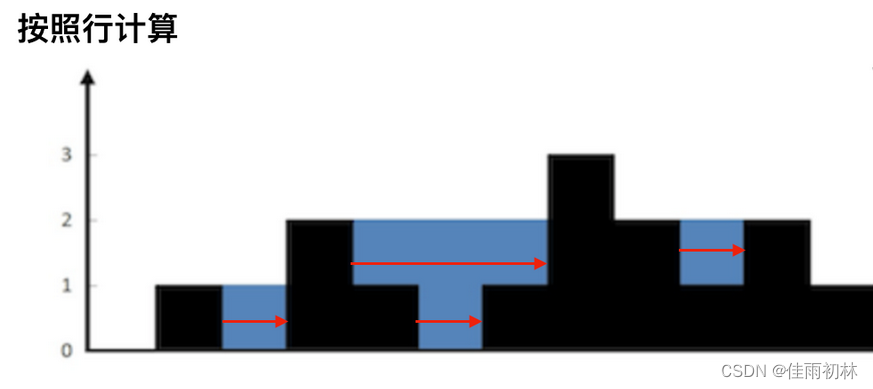
这个题目常见的有两种实现方案,一种是双指针实现,另外一种是单调栈实现,这个两种方法实现的区别就在于前者是按照列为主来计算面积的,后者是以行为主来计算面积。
双指针:通过前缀数组和后缀数组实现寻在某列两侧高度最大的列
# python实现代码,c++实现逻辑也是一样的
class Solution:
def trap(self, height: List[int]) -> int:
n = len(height)
prefix, suffix = [0] * n, [0] * n
# 前缀最大值
prefix[0] = height[0]
for i in range(1, n):
prefix[i] = max(prefix[i - 1], height[i])
# 后缀最大值
suffix[-1] = height[-1]
for i in range(n - 2, -1, -1):
suffix[i] = max(suffix[i + 1], height[i])
# 每一个格子对应能解多少水等于前后缀最大值的中的最小值 - 柱子高度
ans = 0
for h, pre, suf in zip(height, prefix, suffix):
ans += min(pre, suf) - h
return ans
单调栈:单调栈的计算是将每行的面积累加完成的
class Solution {
public:
//单调栈实现
int trap(vector<int>& height) {
stack<int> st;
st.push(0);
int sum = 0;
for(int i = 0; i < height.size(); i++){
while(!st.empty() && height[i] > height[st.top()]){
int mid = st.top();
st.pop();
if(!st.empty()){
int h = min(height[st.top()], height[i]) - height[mid];
int w = i - st.top() - 1;
sum += h * w;
}
}
st.push(i);
}
return sum;
}
};
5.柱状图中最大的矩形
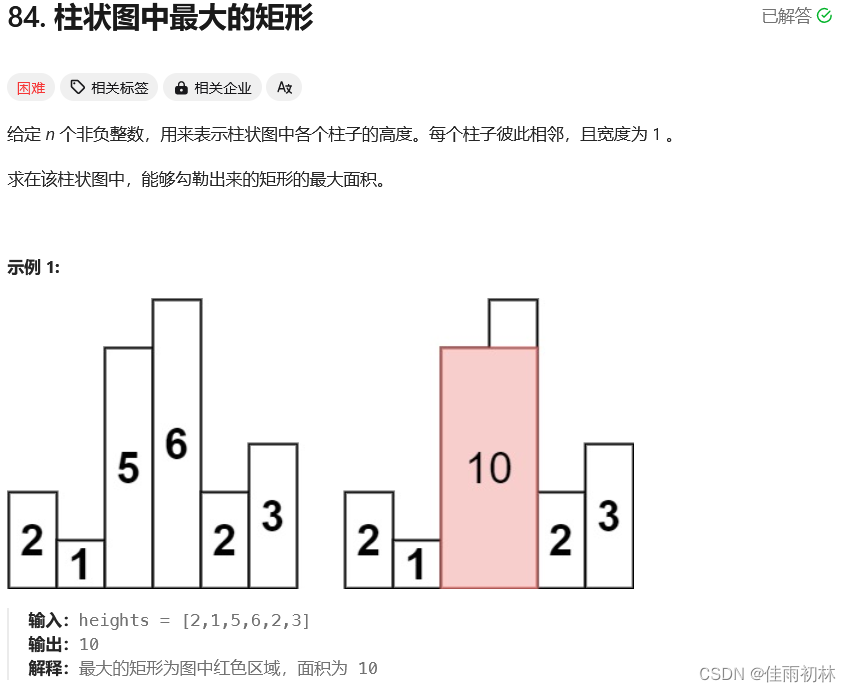 本次的解题思路和上题接雨水是一样的,但是本题中,我们需要关注的是矮的柱子(短板原理),上一题是关注高的柱子。同上有两种解法,下面给出的是单调栈的解法。(这个题目比上个题目要难一点,请注意如何处理收尾使得遍历逻辑连贯)
本次的解题思路和上题接雨水是一样的,但是本题中,我们需要关注的是矮的柱子(短板原理),上一题是关注高的柱子。同上有两种解法,下面给出的是单调栈的解法。(这个题目比上个题目要难一点,请注意如何处理收尾使得遍历逻辑连贯)
class Solution {
public:
int largestRectangleArea(vector<int>& heights) {
stack<int> st;
//首部加入0是为了能够在某升序数组的情况下获得左边界;尾部加入0是为了能够方便循环的进行(能够将所有元素弹出计算)
heights.insert(heights.begin(), 0);//数组头部加入元素0
heights.insert(heights.end(), 0);//数组尾部加入元素0
st.push(0);
int result = 0;
for(int i = 1; i < heights.size(); i++){
while(heights[i] < heights[st.top()]){
int mid = st.top();
st.pop();
int w = i - st.top() - 1;
int h = heights[mid];
result = max(result, w * h);
}
st.push(i);
}
return result;
}
};
文章来源:https://blog.csdn.net/rain_lin2000/article/details/135786242
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
最新文章
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 软件架构之事件驱动架构
- 波奇学Linux:进程等待
- OpenShift 4 - 管理和使用 OpenShift AI 运行环境
- 《ORANGE’S:一个操作系统的实现》读书笔记(三十一)文件系统(六)
- HCIA(终)eNSP网络基础综合实验:静态路由、OSPF动态路由、Telnet连接、NAT地址转换、ACL规则配置
- 基于uniapp封装的card容器 带左右侧两侧标题内容区域
- 【STM32】STM32学习笔记-ADC模数转换器(21)
- 【Nacos专题】Nacos的可扩展命令事件机制的架构设计
- nestjs 装饰器
- TPE-800 PadZ SERIES Integration Guide