【leetcode 2707. 字符串中的额外字符】动态规划 & 字典树
发布时间:2024年01月09日
题目描述
给你一个下标从 0 开始的字符串
s和一个单词字典dictionary。你需要将s分割成若干个 互不重叠 的子字符串,每个子字符串都在dictionary中出现过。s中可能会有一些 额外的字符 不在任何子字符串中。请你采取最优策略分割
s,使剩下的字符 最少 。
动态规划
这是一个比较典型的动态规划问题,只要能够想到利用dp[i]表示s.substr(0,i)(也就时s从0开始,长度为i的子字符串)剩下的字符的最少数量,比较容易就能找到如下规律:
s.substr(0,i)的后缀与dictionary中一个长度为l的单词匹配,那么dp[i] = dp[i - l]。- 如果
s.substr(0,i)与dictionary中所有单词都不匹配,那么个dp[i] = dp[i - 1] + 1。
据此容易写出如下代码:
class Solution {
public:
int minExtraChar(string s, vector<string>& dictionary) {
int s_len = s.size();
vector<int> dp(s_len + 1, 0);
for(int i = 1;i <= s_len;++i) {
dp[i] = dp[i - 1] + 1;
for(auto it = dictionary.begin();it != dictionary.end();++it) {
int w_len = (*it).size();
if(w_len <= i && s.substr(i - w_len, w_len) == *it) {
dp[i] = min(dp[i], dp[i - w_len]);
}
}
}
return dp[s_len];
}
};
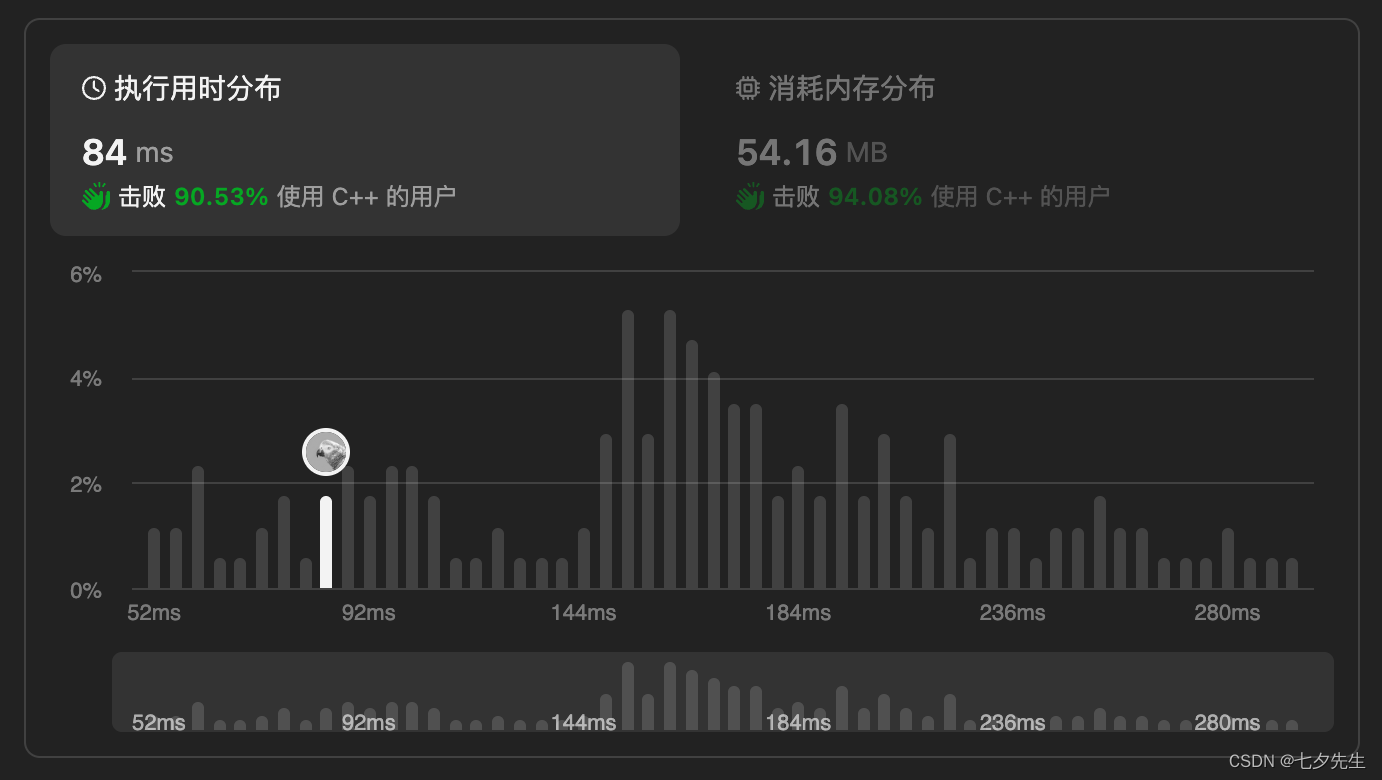
结果还算不错
利用字典树优化
上面思路中提到,要通过字符串的后缀与字典中单词是否匹配来判断动态规划的路径。
这容易让人想到字典树,也就是前缀树。关于字典树,我写过一篇字典树分析及实现。
虽然称为前缀树,经过一些变形也可以用来快速判断后缀是否匹配。
进而优化上面的实现,算是用空间换时间。
代码的改变还是比较大的,具体实现如下
struct Trie {
struct Trie* children[26];
bool isEnd;
Trie() {
isEnd = false;
memset(children, 0, 26 * sizeof(struct Trie*));
}
};
class Solution {
public:
int minExtraChar(string s, vector<string>& dictionary) {
struct Trie *root = new struct Trie();
int s_len = s.size();
vector<int> dp(s_len + 1, 0);
// 插入字典中的单词
for(auto it = dictionary.begin();it != dictionary.end();++it) {
int d_len = it->size();
struct Trie *p = root;
// 倒序插入单词,方便匹配后缀
for(int i = d_len - 1;i >= 0;--i) {
int idx = (*it)[i] - 'a';
if(p->children[idx] == nullptr) {
p->children[idx] = new struct Trie();
}
p = p->children[idx];
}
p->isEnd = true;
}
for(int i = 1;i <= s_len;++i) {
dp[i] = dp[i - 1] + 1;
struct Trie *p = root;
for(int j = i - 1;j >= 0;--j) {
int idx = s[j] - 'a';
if(p == nullptr || p->children[idx] == nullptr) {
// 如果中间有字符不匹配,后续就不可能有更长单词能匹配后缀了
break;
}
p = p->children[idx];
if(p->isEnd) {
dp[i] = min(dp[i], dp[j]);
}
}
}
return dp[s_len];
}
};
结果如下图,虽然时间上有一定提升,但空间占用却增加了一倍
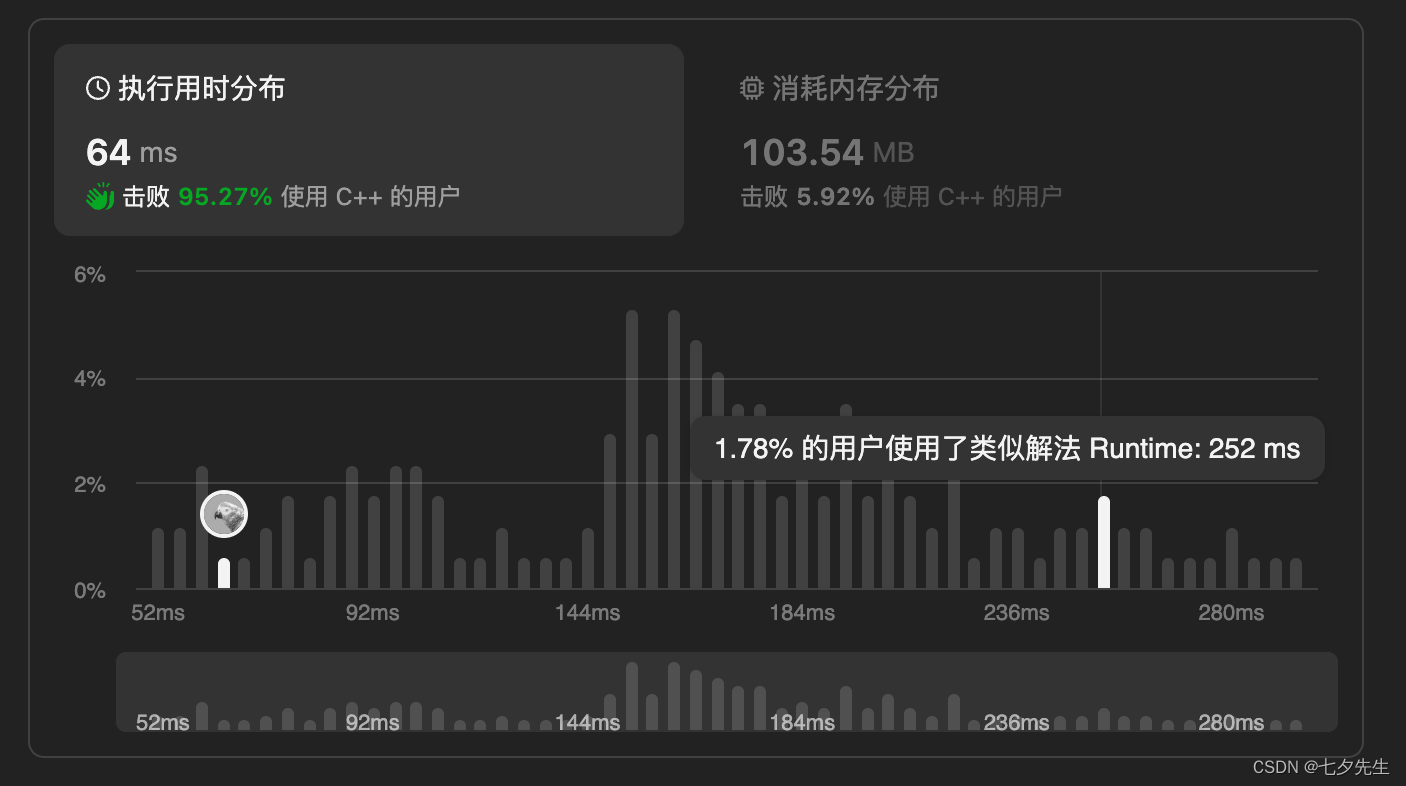
ps:需要注意的是,这里用到了new去动态分配内存,理论上是要利用delete手动释放内存,防止内存泄露的。
文章来源:https://blog.csdn.net/csdnofhaner/article/details/135490747
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
最新文章
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 协程&asyncio&异步编程学习
- 求两个有序整数的交集并输出
- Vue学习笔记11--路由2(路由传参/命名路由)
- Server check fail, please check server xxx.xxx.xxx.xxx,port 9848 is available
- Java基础题4:抽象类和接口
- 如何一键部署本地Java项目到服务器上
- (JAVA)-(网络编程)-初始网络编程
- 【VUE】无法加载文件 \node\vue.ps1,因为在此系统上禁止运行脚本。问题解决
- web站点维护
- 【负载均衡oj】(一)架构和公共模块