【超详细!各版本通用Matlab入门教程】0基础学会可用于毕业论文制图、数学,线代&概率论运算等
发布时间:2024年01月21日
MATLAB
下载、安装方法:
【若未安装环境,可以点击下方链接教程先学习安装,再进行MATLAB入门学习】
点击下方文字:即可跳转MATLAB下载&安装教程
下载&安装MATLAB
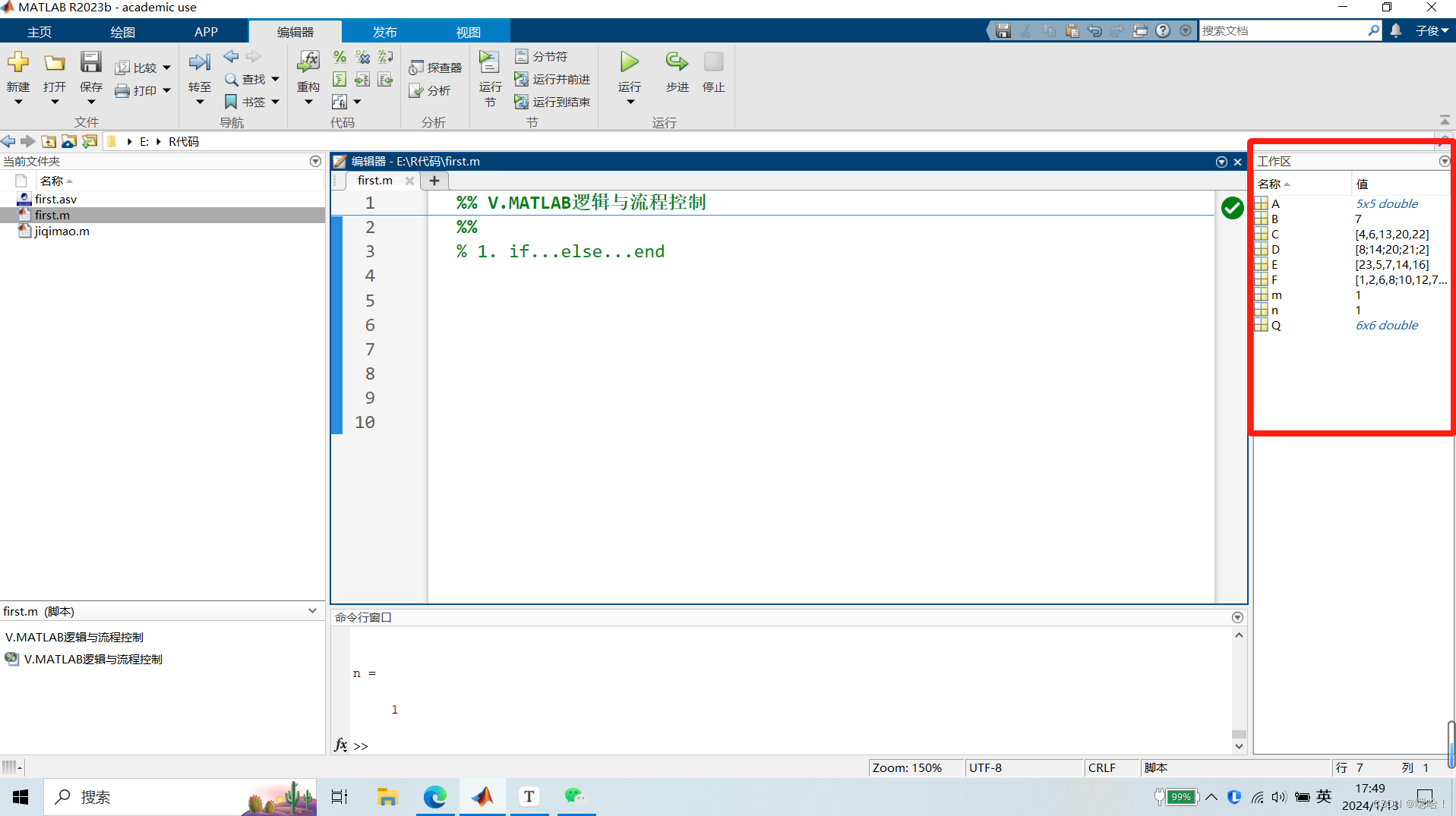
1.常识
1.1注释方法
% 中文内容【注释内容】
%% 段落注释
1.2命令行窗口常见指令
clear all %清空右边工作区的值
clc %清空命令行窗口
2.基础
2.1元胞数组&结构体
E = zeros(10,5,3)
E(:,:,2)=randi(50,10,5)%最大值是50,生成一个10行5列的
E(:,:,3)=randn(10,5)
% 4.元胞数组
A = cell(1,6)
A{2}=eye(3)
A{5}=magic(5)
B=A{5}
% 5.结构体
books=struct('name',{{'hahah','niuma'}},'price',[30,40])
books.name(1)
books.name{1}
2.2矩阵构造&四则运算
%% IV.矩阵操作
%%
% 1.矩阵的定义与构造
A= {1 2 3 5 8 5 4 6}
B=1:3:9 % 从1-9 逐个加3
C=repmat(B,3,1)% 重复3行1列,把B重复
D=ones(2,4)% 全1的矩阵,2行4列
Q=ones(6,6)% 全1的矩阵,6行6列
%%
% 2.矩阵的四则运算
A = [1 2 3 4;5 6 7 8]
B = [1 1 2 2;2 2 1 1]
C = A + B
D=A-B
E=A*B'
F=A.*B
G=A/B
H=A./B
%%
2.3矩阵的下标
%%
% 3.矩阵的下标
A=magic(5)
B=A(2,3)% 取A中第二行第三列【从1开始的】
C=A(3,:)% 取A中第三行所有列【冒号:代表所有的意思】
D=A(:,4)% 取A中第四列所有行【冒号:代表所有的意思】
[m,n]=find(A>20)% 找大于20的序号值/矩阵
%
3.程序结构
3.1三种常见的结构
1.要注意每一个语句都有end
2.switch…case…end 里 不是default 而是 otherwise**

4.绘图
4.1二维平面绘图
%% VII.MATLAB基本绘图操作
%%
% 1.二维平面绘图
x=0:0.01:2*pi;
y=sin(x);
figure % 建立一个幕布
plot(x,y) % 绘制二维图形
title('y=sin(x)') % 取一个标题
xlabel('x') % X的标签
ylabel('sin(x)')% y的标签
xlim([0 2*pi])
x=0:0.01:20;
y1=200*exp(-0.05*x).*sin(x);
y2=0.8*exp(-0.5*x).*sin(10*x);
figure
[AX,H1,h2]=plotyy(x,y1,x,y2,'plot');
set(get(AX(1),'Ylabel'),'String','Slow Decay')
set(get(AX(2),'Ylabel'),'String','Fast Decay')
xlabel('Time(\musec)')
title('MuItiple Decay Rates')
set(H1,'LineStyle','--')
set(H2,'LineStyle',':')
%%
4.2三维立体绘图
%%
% 2.三维立体绘图
t=0:pi/50:10*pi;
plot3(sin(t),cos(t),t)
xlabel('sin(t)')
ylabel('cos(t)')
zlabel('t')
grid on % 添加网格线
axis square % 对图型进行限制变成正方形的样式
%%
4.2.1拓展mesh图像
%%
% mesh图像
[x,y,z]=peaks(30);
mesh(x,y,z)
grid
5.论文图形导出
5.1错误做法
直接截屏法【该方法,图片不清晰,完全没有必要】
5.2正确做法
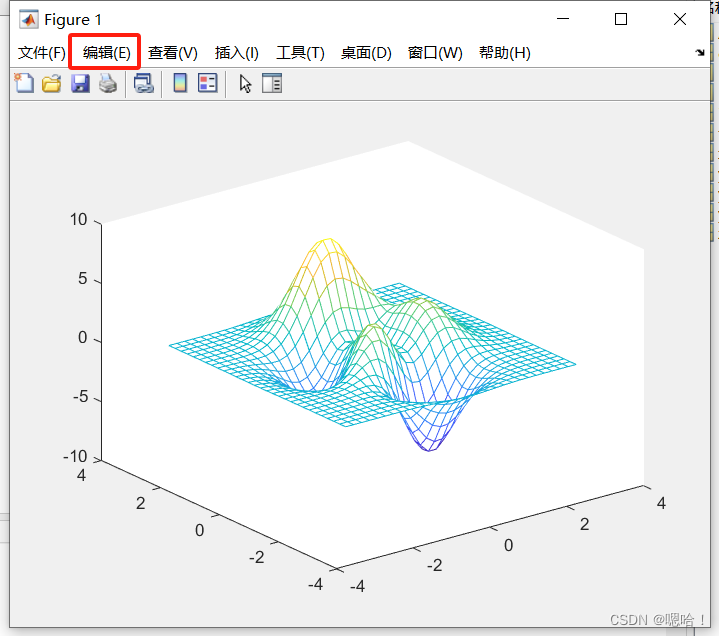
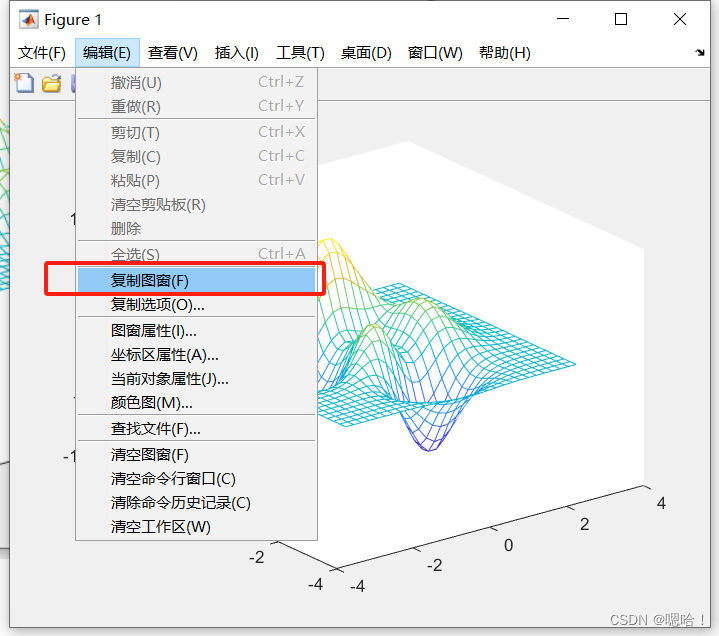
编辑——>复制图窗——>到word粘贴
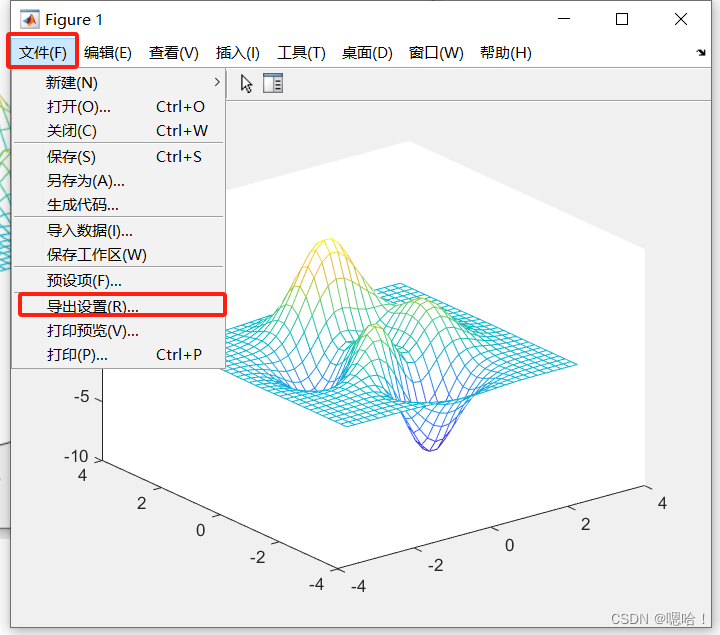
5.3调整图像大小
导出设置中可以调整图像大小
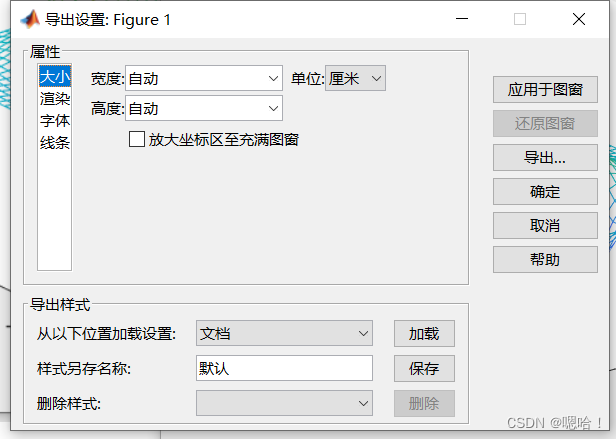
5.4调整参数
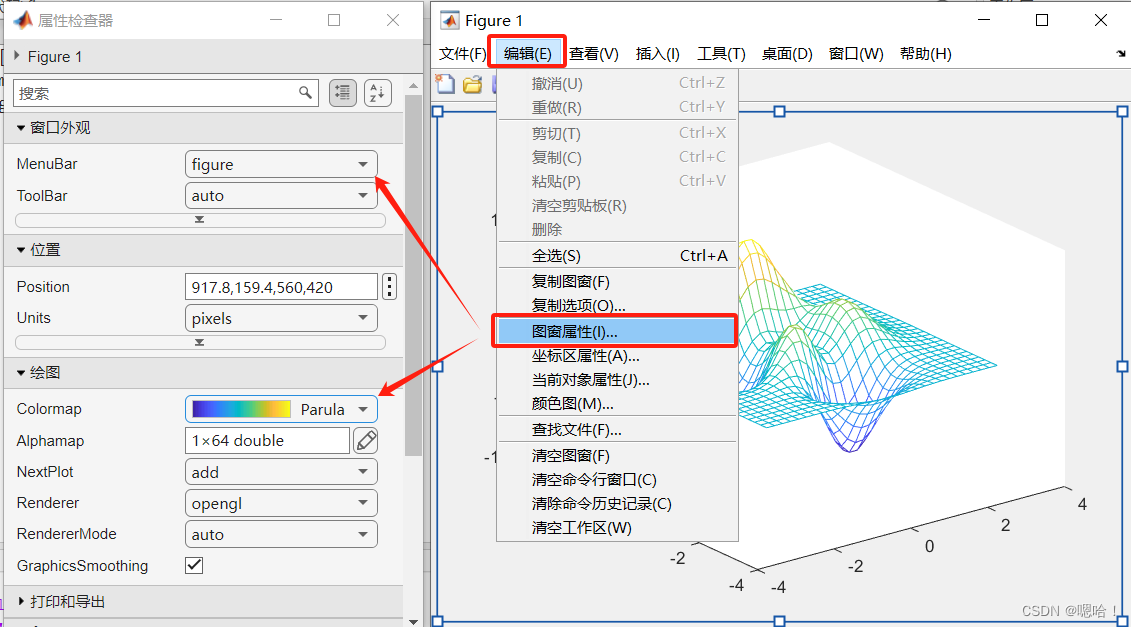
文章来源:https://blog.csdn.net/m0_57495651/article/details/135724774
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!