visual Studio MFC 平台实现图片的傅里叶变换

图片的傅里叶变换

本文主要讲解傅里叶变换的基本数学概念与物理概念，并本文使用visual Studio MFC 平台实现对傅里叶变换在图片上进行了应用。

一、傅里叶变换的原理

在这里推荐一篇讲得非常形象的文章通俗讲解：图像傅里叶变换

1.1 傅里叶变换原理的说明

傅里叶变换是一种数学变换，它将一个函数（可以是时域中的信号或空域中的图像）转换为频域中的表示，从而揭示了信号或图像中存在的不同频率成分。在图像处理中，我们通常使用二维傅里叶变换来处理二维图像。

对于一幅图像而言，傅里叶变换将图像从空域（像素点的位置）转换到频域（不同频率的成分）。频域中的信息描述了图像中不同空间频率的变化。这对于分析图像中的纹理、边缘以及其他特征非常有用。

傅里叶变换的结果可以分解为振幅谱和相位谱。振幅谱表示了图像中不同频率成分的强度，而相位谱表示了这些频率成分的相位信息。

在图像处理中，傅里叶变换常常用于频域滤波、图像增强、压缩等应用。傅里叶变换的逆变换可以将频域表示转换回空域，因此我们可以在频域中进行操作后再通过逆变换得到处理后的图像。

从纯粹的数学意义上看，傅里叶变换是将一个图像函数转换为一系列周期函数来处理的；
从物理效果看，傅里叶变换是将图像从空间域转换到频率域，其逆变换是将图像从频率域转换到空间域。即傅里叶变换的物理意义是将图像的灰度分布函数变换为图像的频率分布函数，傅里叶逆变换是将图像的频率分布函数变换为灰度分布函数。

实际上对图像进行二维傅里叶变换得到频谱图就是图像梯度的分布图，傅里叶频谱图上看到的明暗不一的亮点，实际上图像上某一点 与邻域点差异的强弱，即梯度的大小，即该点的频率大小。
如果频谱图中暗的点数更多，则实际图像是比较柔和的；反之，如果频谱图中亮的点数多，则实际图像是比较尖锐的，边界分明且边界两边像素差异较大。

以下是对一些关键概念的简要总结：

1. 数学意义： 傅里叶变换是一种将一个信号（包括图像）从时间域（或空间域）转换为频率域的方法。它将一个信号分解为一组正弦和余弦函数（频率分量），以揭示信号中的不同频率成分。

2. 物理效果： 傅里叶变换的物理效果是将图像从空间域（表示像素在图像中的位置）转换为频率域（表示图像中不同频率的成分）。逆傅里叶变换则将频率域的信息重新转换为空间域，从而实现对原始图像的还原。

3. 频谱图： 傅里叶变换的结果通常以频谱图的形式呈现，其中显示了图像在频率域中的分布。频谱图中的亮度表示不同频率成分的强度，而频谱图上的点对应于不同的频率。

4. 梯度分布： 在频谱图中，明暗不一的亮点对应于图像中不同频率的变化。较暗的区域表示较低频率的成分，而较亮的区域表示较高频率的成分。这与图像的梯度（差异）有关，因为梯度较大的区域通常对应于频谱图中较亮的部分。

总体而言，傅里叶变换为我们提供了一种在频率域中理解图像特征的工具，有助于分析图像的纹理、边缘和其他结构。这对于许多图像处理任务，如滤波、增强和压缩，都是非常有用的。

1.2 数学表达

1.2.1 傅里叶变换的数学表示

对于一个连续函数 $f(t)$其傅里叶变换 $F(w)$ 定义为：

$$F(w)={\int }_{?\infty }^{\infty }f(t)?e^{?iwt}dt$$

其中，$F(w)$表示频率为$w$的成分的复幅度，$e^{?iwt}$ 是复指数函数， $t$ 是时间。

1.2.2 傅里叶逆变换的数学表示

傅里叶变换的逆过程是傅里叶逆变换，它将频率域表示还原为时间或空间域表示。对于一个频谱 $F(w)$，其逆变换 $f(t)$ 定义为：

$$f(t)=\frac{1}{2\pi }{\int }_{?\infty }^{\infty }F(w)?e^{iwt}dw$$

1.2.3 离散傅里叶变换（DFT）的数学表示

在数字信号处理中，通常使用离散傅里叶变换。对于一个离散序列 $x[n]$，其离散傅里叶变换 $X[k]$ 定义为：

$$X[k]=\sum _{n=0}^{N?1}x[n]?e^{?i\frac{2\pi }{N}kn}$$

其中， $N$ 是序列的长度， $X[k]$ 表示频率为 $\frac{k}{N}$ 的成分的复幅度。

1.3 傅里叶变换的应用

1. 频域分析： 傅里叶变换允许我们在频域中分析信号，找到不同频率的成分。

2. 滤波： 在频域中进行滤波操作，去除或增强特定频率的成分。

3. 信号压缩： 将信号在频域中表示通常可以更紧凑地表示信号。

4. 图像处理： 在图像处理中，傅里叶变换常用于分析和处理图像的频率成分。

总的来说，傅里叶变换是一种非常强大的数学工具，广泛应用于信号处理、通信、图像处理等领域。

二、 傅里叶变换与快速傅里叶变换的区别

傅里叶变换（Fourier Transform）和快速傅里叶变换（Fast Fourier Transform, FFT）是两种相关但不同的数学算法，用于在信号处理、图像处理等领域分析信号的频域特征。

1. 傅里叶变换：

   • 定义： 傅里叶变换是一种将信号从时域（时间域）转换到频域（频率域）的数学变换。对于连续信号，傅里叶变换的定义是积分形式；对于离散信号，傅里叶变换的定义是离散形式。
   • 计算复杂度： 对于 N 个数据点的信号，傅里叶变换的计算复杂度是 O(N^2)，其中 N 是数据点的数量。

2. 快速傅里叶变换（FFT）：

   • 定义： FFT 是一种优化算法，用于高效地计算傅里叶变换。FFT 算法可以在 O(N log N) 的时间内完成信号的傅里叶变换，相较于传统的傅里叶变换算法，FFT 算法速度更快。
   • 计算复杂度： FFT 的计算复杂度相对较低，使得在计算机上更容易处理大规模的数据。

总结区别：

• FFT 是一种特定的傅里叶变换算法，它是为了提高傅里叶变换的计算速度而设计的。
• 傅里叶变换是一般性的概念，可以用于描述信号在频域中的表示；FFT 是实现傅里叶变换的具体算法。
• FFT 的主要优势在于其计算速度，尤其是对于大规模数据的情况，它比传统傅里叶变换更为高效。

在实际应用中，由于 FFT 算法的高效性，它通常是首选的频域分析工具。很多信号处理库和软件包中都包含了 FFT 的实现，使得工程师和科学家能够更方便地进行频域分析。

三、 绘制傅里叶变换的频谱

因为要使用opencv的库所以visual Studio没有配置opencv的，需要先配置一下，可以参考博客Visual Studio 配置opencv环境

#include <opencv2/opencv.hpp>
#include <opencv2/highgui/highgui.hpp>
#include <opencv2/imgproc/imgproc.hpp>
#include <opencv2/core.hpp>

using namespace cv;
// 中心化频谱函数
void fftShift(Mat& mag)
{
 int cx = mag.cols / 2;
 int cy = mag.rows / 2;

 Mat q1(mag, cv::Rect(0, 0, cx, cy));
 Mat q2(mag, cv::Rect(cx, 0, cx, cy));
 Mat q3(mag, cv::Rect(0, cy, cx, cy));
 Mat q4(mag, cv::Rect(cx, cy, cx, cy));

 Mat tmp;
 q1.copyTo(tmp);
 q4.copyTo(q1);
 tmp.copyTo(q4);

 q2.copyTo(tmp);
 q3.copyTo(q2);
 tmp.copyTo(q3);
}
//FFT傅里叶变换
void CMFCApplication1View::OnFft()
{
 // TODO: 在此添加命令处理程序代码
 
 if (gray_data != nullptr) {
  // 将灰度数据转换为OpenCV的Mat对象，图像尺寸为bmpHeight x bmpWidth，数据类型为8位无符号整数
  Mat image(bmpHeight, bmpWidth, CV_8U, gray_data);

  // 执行傅里叶变换
  Mat padded; // 扩展输入图像到最佳尺寸
  int m = getOptimalDFTSize(image.rows);
  int n = getOptimalDFTSize(image.cols);
  copyMakeBorder(image, padded, 0, m - image.rows, 0, n - image.cols, BORDER_CONSTANT, Scalar::all(0));//在图像周围填充零

  // 为频域图像分配内存
  Mat planes[] = { Mat_<float>(padded), Mat::zeros(padded.size(), CV_32F) };//存储频域表示的复杂图像
  Mat complexImage;
  merge(planes, 2, complexImage);

  // 执行傅里叶变换,从空间域转换到频域。
  dft(complexImage, complexImage);

  // 分离实部和虚部,存储在planes数组中
  split(complexImage, planes);

  // 计算幅度谱,将结果存储在planes数组的第一个平面
  magnitude(planes[0], planes[1], planes[0]);

  // 变换到对数尺度     //对幅度谱进行对数变换以增强可视化效果
  planes[0] += Scalar::all(1);
  log(planes[0], planes[0]);

  // 归一化到 [0, 1]
  normalize(planes[0], planes[0], 0, 1, NORM_MINMAX);

  // 显示未中心化的频谱图
  imshow("Spectrum (Uncentered)", planes[0]);

  // 中心化频谱
  fftShift(planes[0]);

  // 显示中心化后的频谱图
  imshow("Spectrum (Centered)", planes[0]);

  waitKey(0);//等待按键操作,然后关闭图像窗口
 }
 else {
  // 处理图像未加载的情况
  AfxMessageBox(_T("未加载灰度图片"));
 }
}

说明：dft(complexImage, complexImage); 这一行执行的傅里叶变换，调用了OpenCV中的dft函数，对输入的complexImage执行傅里叶变换。在这个上下文中，dft是一个通用的傅里叶变换函数，而非专门的FFT实现。由于OpenCV中的dft函数使用了优化算法，它实际上在内部采用了FFT来提高计算效率，但在代码层面上，我们通常将其称为傅里叶变换。

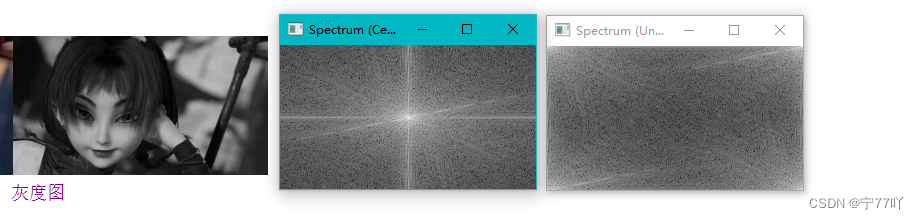
左：灰度图 中：进行中心化后的频谱图 右：未中心化的频谱图