【MATLAB】PSO粒子群优化BiLSTM（PSO_BiLSTM）的时间序列预测

有意向获取代码，请转文末观看代码获取方式~也可转原文链接获取~

1 基本定义

基于PSO粒子群优化的BiLSTM的时间序列预测算法的基本原理如下：

1. 「双向长短时记忆（BiLSTM）模型」：这是一种深度学习模型，特别适用于处理时序数据。BiLSTM模型能够同时捕捉时间序列数据的长期依赖关系和短期模式，从而在时间序列预测中表现出色。

2. 「粒子群优化（PSO）算法」：这是一种优化算法，通过模拟鸟群觅食行为来寻找最优解。PSO通过个体和群体信息的交互，引导粒子（在这里指的是BiLSTM模型参数的组合）向最优解的方向移动。

3. 「PSO-BiLSTM结合」：将PSO算法与BiLSTM模型结合，通过PSO搜索BiLSTM模型的参数空间，以找到最佳的参数组合，从而提高预测性能。在PSO-BiLSTM中，每个粒子代表一个BiLSTM模型，并根据其在参数空间中的位置和速度来调整模型的参数。

4. 「训练过程」：首先，为每个粒子（即一组LSTM参数）设定初始位置和速度。然后，对于每个粒子，使用当前的参数配置构建BiLSTM模型，对训练数据进行预测。预测误差（通常使用均方误差MSE等指标）即为该粒子的适应度值。接着，基于粒子的历史最佳位置和全局最佳位置，更新粒子的速度和位置。这个过程会重复进行，直到满足停止条件（如达到预设的最大迭代次数，或适应度值达到预设阈值等）。在每次迭代中，都会更新粒子的位置和速度，并重新评估适应度值。最后，选择全局最佳位置对应的参数组合作为PSO-BiLSTM模型的最终参数。

5. 「预测阶段」：在训练完成后，使用得到的全局最优参数配置构建最终的BiLSTM模型，并对测试数据进行预测。

6. 「模型架构」：

   • 「输入层」：接收时间序列数据作为输入。

   • 「BiLSTM层」：使用双向LSTM单元捕捉时间序列中的长期和短期依赖关系。

   • 「全连接层」：将BiLSTM层的输出转换为预测值。

7. 「PSO参数设置」：

   • 「粒子数量」：决定了搜索空间的覆盖范围和计算复杂度。

   • 「速度和位置更新公式」：决定了粒子在参数空间中的移动方式。

   • 「惯性权重」：用于平衡粒子的全局和局部搜索能力。

8. 「性能评估」：

   • 使用各种性能指标（如均方误差、均方根误差、平均绝对误差等）来评估模型的预测性能。

   • 可以通过与其他基准模型（如单一的LSTM、ARIMA等）进行比较，来验证PSO-BiLSTM模型的优越性。

9. 「应用领域」：

   • 这种算法可以应用于各种时间序列预测问题，如股票价格预测、气象预测、交通流量预测等。

10. 「优势和挑战」：

• 「优势」：

  • 能够自动寻找BiLSTM模型的最佳参数组合，减少手动调参的工作量。

  • 结合了BiLSTM的序列建模能力和PSO的全局优化能力，通常能够获得较好的预测性能。

• 「挑战」：

  • PSO算法可能陷入局部最优解，导致无法找到全局最优参数。

  • 对于大规模数据集和高维参数空间，PSO-BiLSTM的计算成本可能较高。

  • 「未来研究方向」：

• 探索更有效的粒子初始化策略，以提高搜索效率。

• 研究更先进的PSO变体，以提高优化性能。

• 结合其他深度学习模型或集成学习方法，进一步提高预测精度。

• 应用于更多复杂和多变的时间序列预测任务，验证算法的实际应用价值。

2 出图效果

附出图效果如下：

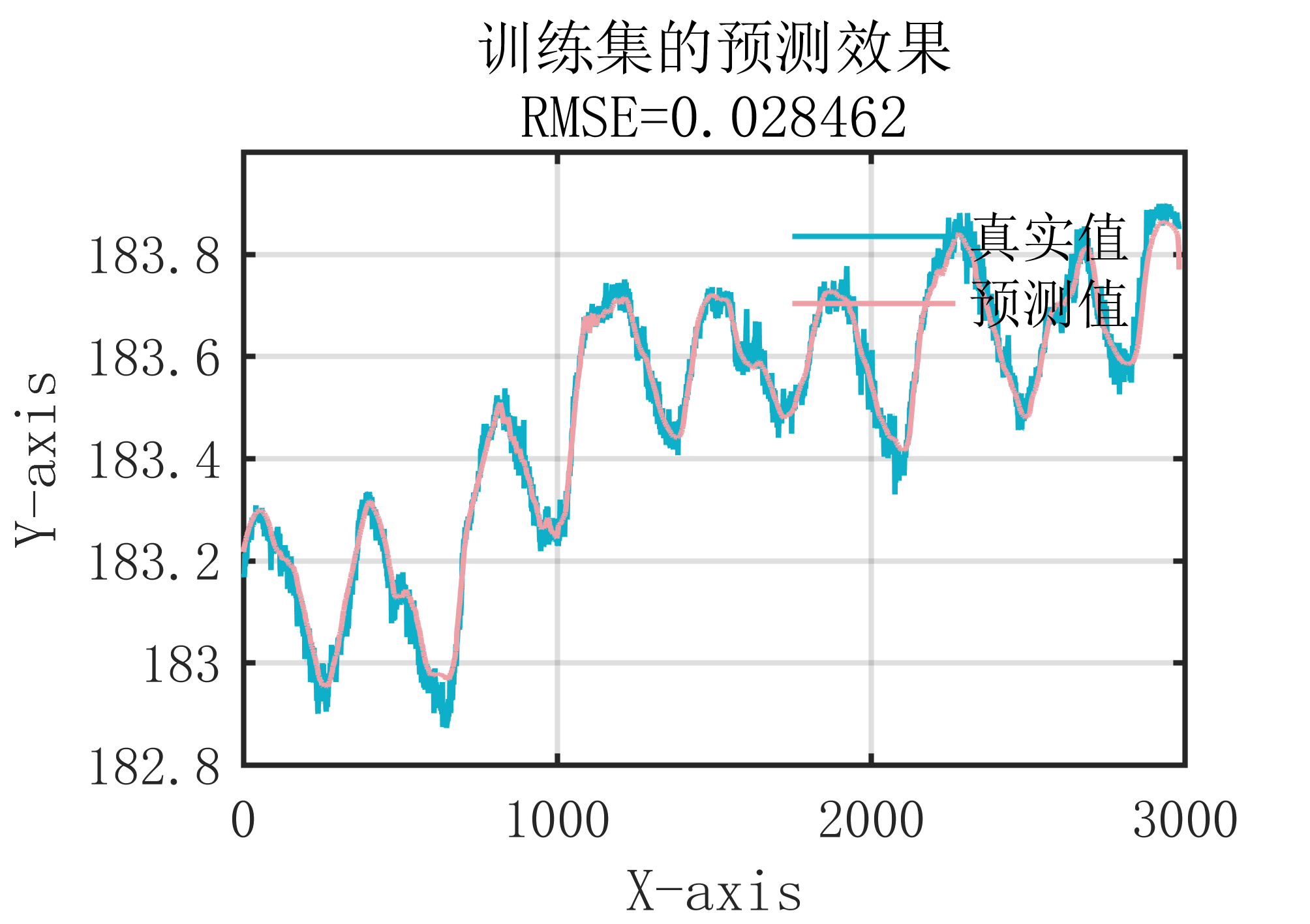
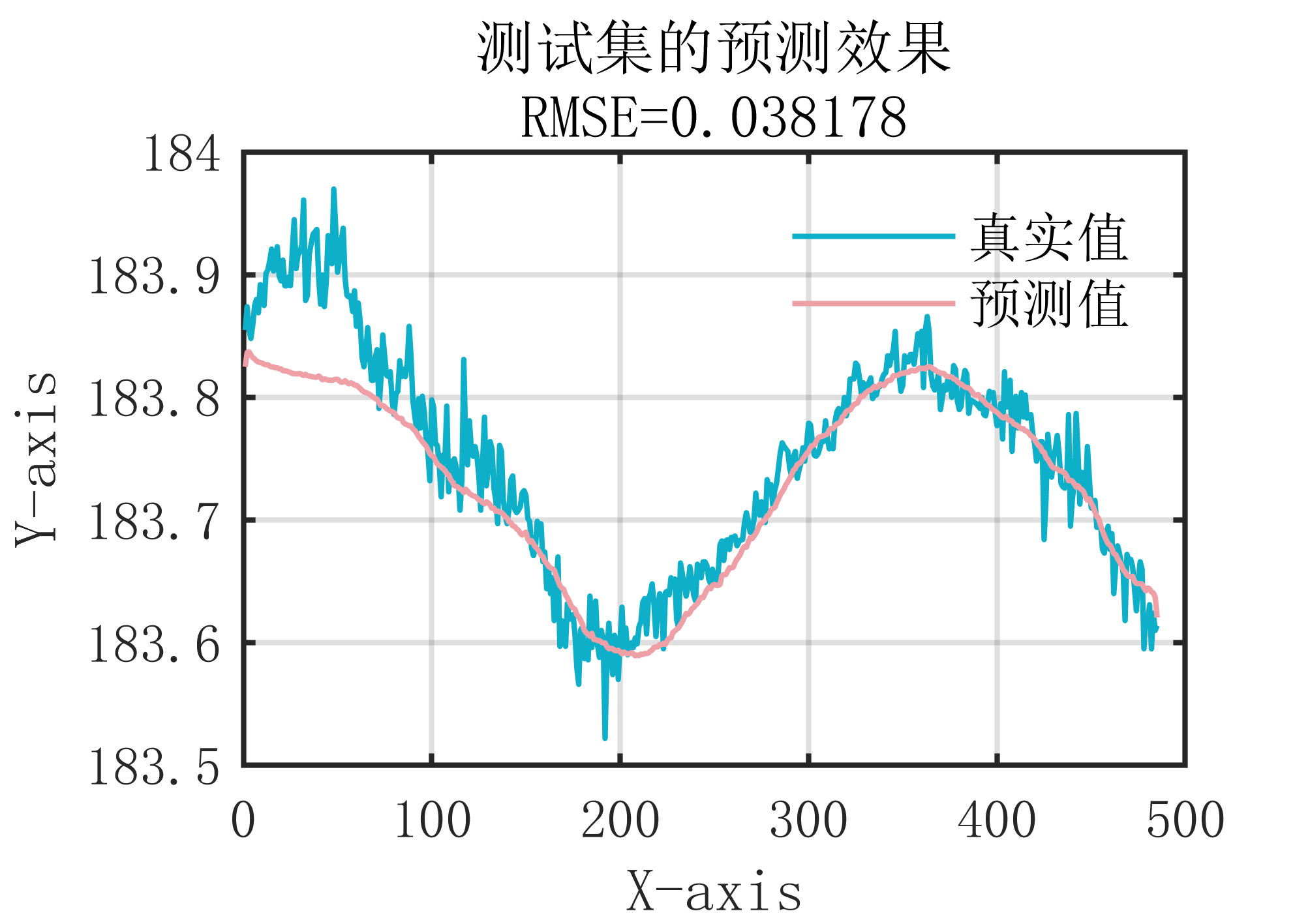
附视频教程操作：