转动惯量与惯性张量 的推导

从牛顿第二定律推出绕固定轴旋转的转动惯量，再用类似方法从牛顿第二定律推出绕固定点转动的惯性张量

基础定义

角速度$\omega$是一个三维向量，方向表示旋转轴，用右手定则代表旋转方向，长度代表旋转弧度的速度

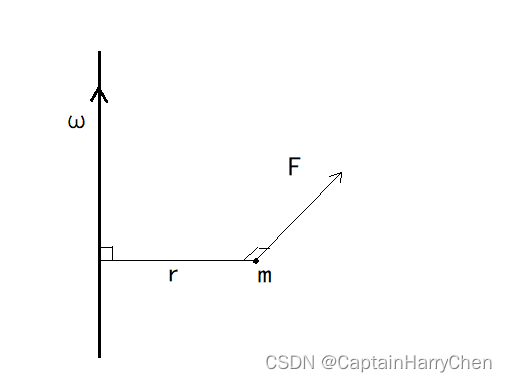
线速度：$v=\omega \times r$ ，其中$r$代表旋转轴或旋转中心点到质点的垂直连线 $r\perp \omega$

角加速度为 $\alpha =\frac{d\omega }{dt}$ ，加速度为 $a=\frac{dv}{dt}$，可推出 $a=\alpha \times r$

牛顿第二定律 $F=ma$，$m$为质点质量

力矩：$\tau =r\times F$，可以相加

绕固定轴 转动惯量推导

在旋转中，平动的力相当于旋转的力矩，平动的线加速度相当于角加速度，质量则代表平动的惯性，那么转动的惯性即为转动惯量
需要找到一个量乘以加速度为该质点所受总力矩

在固定转轴的旋转中，只有$F\perp r$的分力有作用，故只考虑这种力

$$\begin{array}{rl}F& =ma=m\alpha \times r\\ \tau & =r\times F=m?(r\times \alpha \times r)\\ 因为& r\perp \alpha ,则r\times \alpha \times r=||r|{|}^2\alpha \\ \tau & =m||r|{|}^2\alpha \end{array}\text{\hspace{1em}?}$$

将物体的每一个质点积分起来，则可定义转动惯量为$J=\int ||r|{|}^{2}dm$，$\tau =J\alpha$，与牛顿第二定律$F=ma$对应
物理模拟时可用力矩算出角速度变化量

绕固定点 惯性张量推导

对于任意刚体，施加在刚体上的力$F$可以分解为重心到力作用点的方向$F_1$和垂直于该方向的力$F_2$，可以认为在这一瞬间，只有$F_1$会移动该物体，没有旋转作用，$F_2$只对物体具有旋转作用

现在考虑旋转，故只考虑$F_2$，假设$r$为重心到力作用点连线，$m$为该位置质点质量，$F\perp r$
刚体最终的旋转由所有力矩加和决定，故对于单一的一个质点所对应的$r$，不满足$r\perp \alpha$

需要找到一个量乘以加速度为该刚体所受总力矩

$$\begin{array}{rl}F& =ma=m\alpha \times r\\ \tau & =r\times F=m?(r\times \alpha \times r)\end{array}\text{\hspace{1em}?}$$

此时$r$不垂直于$\alpha$，则$(r\times \alpha \times r)$需要中展开计算

$$\begin{gathered} r\times \alpha \times r=\left[\begin{array}{c}{r}_2{\alpha }_3?r_3{\alpha }_2\\ r_3{\alpha }_1?r_1{\alpha }_3\\ r_1{\alpha }_2?r_2{\alpha }_1\end{array}\right]\times \left[\begin{array}{c}{r}_1\\ r_2\\ r_3\end{array}\right]=\left[\begin{array}{c}{r}_3^2{\alpha }_1?r_1{r}_3{\alpha }_3?r_1{r}_2{\alpha }_2+r_2^2{\alpha }_1\\ r_3^2{\alpha }_2?r_1{r}_2{\alpha }_1?r_2{r}_3{\alpha }_3+r_1^2{\alpha }_2\\ r_2^2{\alpha }_3?r_2{r}_3{\alpha }_2?r_1{r}_3{\alpha }_1+r_1^2{\alpha }_3\end{array}\right] \\ =\left[\begin{array}{ccc}{r}_2^2+r_3^2& ?r_1{r}_2& ?r_1{r}_3\\ ?r_1{r}_2& r_1^2+r_3^2& ?r_2{r}_3\\ ?r_1{r}_3& ?r_2{r}_3& r_1^2+r_2^2\end{array}\right]?\left[\begin{array}{c}{\alpha }_1\\ {\alpha }_2\\ {\alpha }_3\end{array}\right]=I\alpha \end{gathered}$$
将每一个质点积分起来，可以得到惯性张量
$$令I=\int \left[\begin{array}{ccc}{r}_2^2+r_3^2& ?r_1{r}_2& ?r_1{r}_3\\ ?r_1{r}_2& r_1^2+r_3^2& ?r_2{r}_3\\ ?r_1{r}_3& ?r_2{r}_3& r_1^2+r_2^2\end{array}\right]dm为惯性张量$$
则$\tau =I\alpha$，与牛顿第二定律$F=ma$对应

令$r=(xyz{)}^T$，就可以得到惯性张量的经典定义
$$\begin{gathered} 令I=\left[\begin{array}{ccc}{I}_{xx}& I_{xy}& I_{xz}\\ I_{yx}& I_{yy}& I_{yz}\\ I_{zx}& I_{zy}& I_{zz}\end{array}\right] \\ {I}_{xx}=\int (y^2+z^2)dm \\ {I}_{xy}=I_{yx}=?\int xydm \\ 其余同理 \end{gathered}$$
并且可以得到$I=\int ((r^T?r)1?r?r^T)dm$，其中$1$为单位矩阵

注意到$I$会随着刚体的旋转而变化，不太好用，但是存在一个转换公式

假设物体最开始惯性张量为$I_{body}$，在应用了旋转矩阵$R$之后

惯性张量将变为
$$\begin{array}{rl}I& =\int ((r^T{R}^T?Rr)1?Rr?r^T{R}^T)dm\\ & =\int ((r^{T}r)1?Rr?r^T{R}^T)dm\\ & =\int ((r^{T}r)R?1?R^T?Rr?r^T{R}^T)dm\\ & =R\left(\int ((r^{T}r)1?r?r^T)dm\right)R^T\\ & =R{I}_{body}{R}^T\end{array}\text{\hspace{1em}?}$$
如此就方便转换了，而惯性张量可以在刚体初始时计算出来

物理模拟时，可以统计作用在一个刚体上的力矩加和，再求惯性张量的逆，可以算出角速度变化量