数据结构(2023-2024)
一、判断题
1.队列是一种插入和删除操作分别在表的两端进行的线性表,是一种先进后出的结构。(F)
队列先进先出,在表的一端插入元素,在表的另一端删除元素。允许插入的一端称为队尾(rear),允许删除的一端称为队头(front)
2.?栈是插入和删除只能在一端进行的线性表;队列是插入在一端进行,删除在另一端进行的线性表。(T)
3.算法和程序没有区别,在数据结构中二者是通用的。(F)
算法是用来描述数据对象之间的关系,包括数据的逻辑关系和存储关系
语言是描述算法的工具
程序是算法在计算机中的实现。程序设计的实质是对实际问题选择一种好的数据结构,加之设计一个好的算法,而好的算法在很大程度上取决于描述实际问题的数据结构。
算法和程序是有区别的
4.?对于顺序存储的长度为N的线性表,删除第一个元素和插入最后一个元素的时间复杂度分别对应为O(1)和O(N)。(F)
插入最后一个元素的时间复杂度为O(1)
若某线性表最常用的操作是存取任一指定序号的元素和在最后进行插入和删除运算,则利用顺序表存储最节省时间。(T)
5.?线性表采用链式存储表示时,所有结点之间的存储单元地址可以连续也可以不连续。(T)
6.已知一棵二叉树的先序遍历结果是ABC, 则CAB不可能是中序遍历结果(T)
7.具有10个叶结点的二叉树中,有9个度为2的结点。(T)
具有10个叶节点,则度为2的结点为10-1=9
8.?在含有n个结点的树中,边数只能是n-1条。(T)
9.完全二叉树中,若一个结点没有左孩子,则它必是树叶。(T)
若一个结点没有左孩子,也必定没有右孩子,所以必定为树叶
10. (N^2)*logN和Nlog(N^2)具有相同的增长速度。(F)
N*N*log(N)? ?N*logN
N*2*log(N)? ? 2*logN
N 和2相差较大
11.?Nlog(N^2)和N(logN)具有相同的增长速度。(T)
2*NlogN? ?NlogN
2? ? ? ? ? ? ? ? ?1
相差不大
12.?一棵有124个结点的完全二叉树,其叶结点个数是确定的。(T)
13.将一棵完全二叉树存于数组中(根结点的下标为1)。则下标为23和24的两个结点是兄弟。(F)
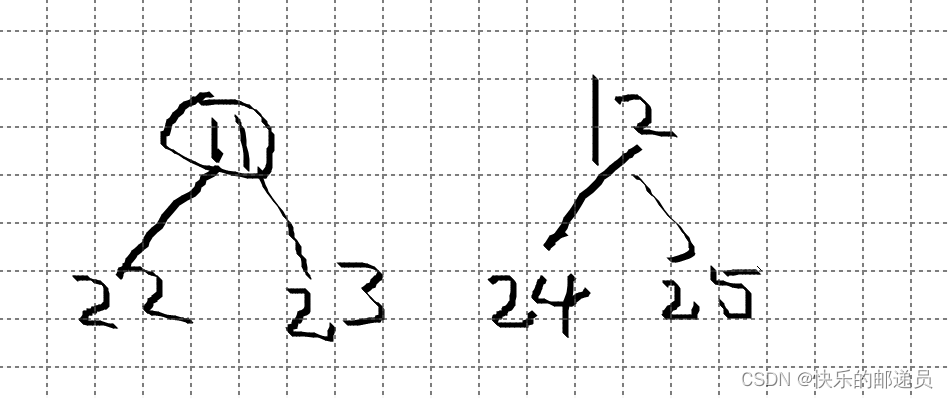
23/2=11
24/2=12
13.?循环队列执行出队操作时会引起大量元素的移动。(F)
循环队列执行出队操作时不会引起大量元素移动
14.?队列中允许插入的一端叫队头,允许删除的一端叫队尾)(F)
队列在队尾插入,在队头删除
15.?队列结构的顺序存储会产生假溢出现象(T)
循环队列可以用来解决假溢出的现象
二、单选题
1.一棵树可转换成为与其对应的二叉树,则下面叙述正确的是(A)。
A.树的先根遍历序列与其对应的二叉树的先序遍历相同
B.树的后根遍历序列与其对应的二叉树的后序遍历相同
C.树的先根遍历序列与其对应的二叉树的中序遍历相同
D.以上都不对
树的先根遍历等价于二叉树的先序遍历
树的后跟遍历等价于二叉树的中序遍历
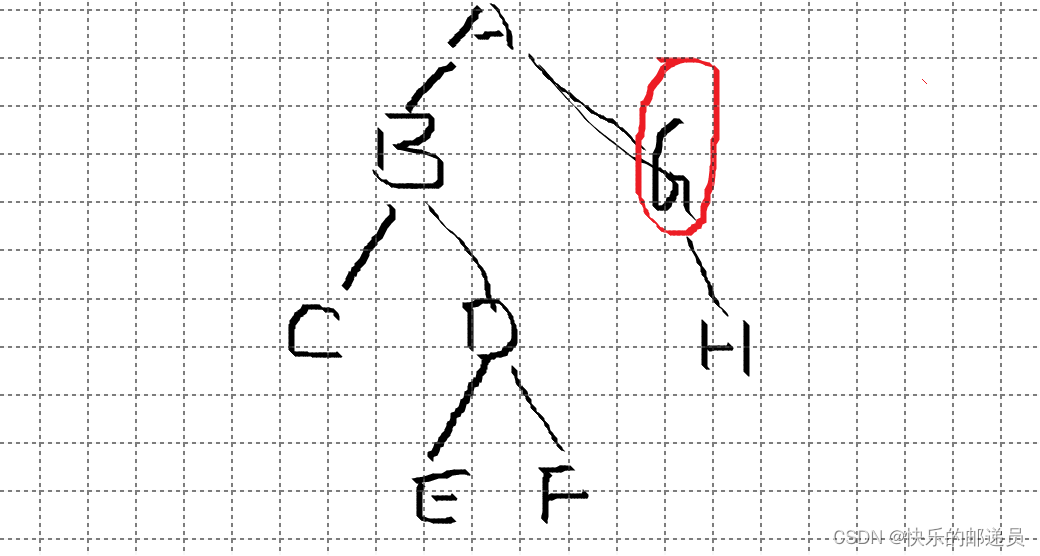
2.?已知二叉树的先序遍历序列为ABCDEFGH,中序遍历序列为CBEDFAGH,则该二叉树形态中,父节点的右子节点为(C)。
A.D
B.H
C.G
D.F
3.?在任何一棵二叉树中,若结点a有左孩子b、右孩子c,则在结点的先序序列、中序序列、后序序列中,( C)。
A.结点b一定在结点a的前面
B.结点a一定在结点c的前面
C.结点b一定在结点c的前面
D.结点a一定在结点b的前面
先序:abc
中序:bac
后序:bca
b一定在c前面
4.?下面程序段的时间复杂度是(A)。

A.O(1)
B.O(N)
C.O(N2)
D.O(log2?N)
循环中并没有出现关于n的for循环,所以为o(1)
5.?下列函数中,哪个函数具有最慢的增长速度:(B)
A.N^1.5
B.Nlog(N^2)
C.(N^2)logN
D.N((logN)^2)
B.2NlogN
C.N*N*logN
D.N*logN*logN
同除NlogN,B=2 C=N? D=logN?
6.下列函数中,哪两个函数具有相同的增长速度:(D)
A.2^N和N^N
B.N和2/N
C.(N^2)logN和Nlog(N^2)
D.Nlog(N^2)和NlogN
C.N*NlogN? 2NlogN,同除NlogN? ? N? ?2
D.2NlogN? ? NlogN? ?同除NlogN? ? 2? ?1
7.?在双向循环链表结点p之后插入s的语句是:(D)
A.p->next=s; s->prior=p; p->next->prior=s ; s->next=p->next;
B.p->next->prior=s; p->next=s; s->prior=p; s->next=p->next;
C.s->prior=p; s->next=p->next; p->next=s; p->next->prior=s;
D.s->prior=p; s->next=p->next; p->next->prior=s; p->next=s;
8.以二叉链表作为二叉树的存储结构,在具有?n?个结点的二叉链表中(n>0),空链域的个数为 __(A)
A.n+1
B.n
C.n?1
D.无法确定
空链域为n+1个,非空链域为n-1个
9.?已知二叉树的前序遍历序列为 ABDCEFG,中序遍历序列为 DBCAFEG,则后序遍历序列为 __(B)
A.BDACEFG
B.DCBFGEA
C.ABCDEFG
D.GFEDCBA
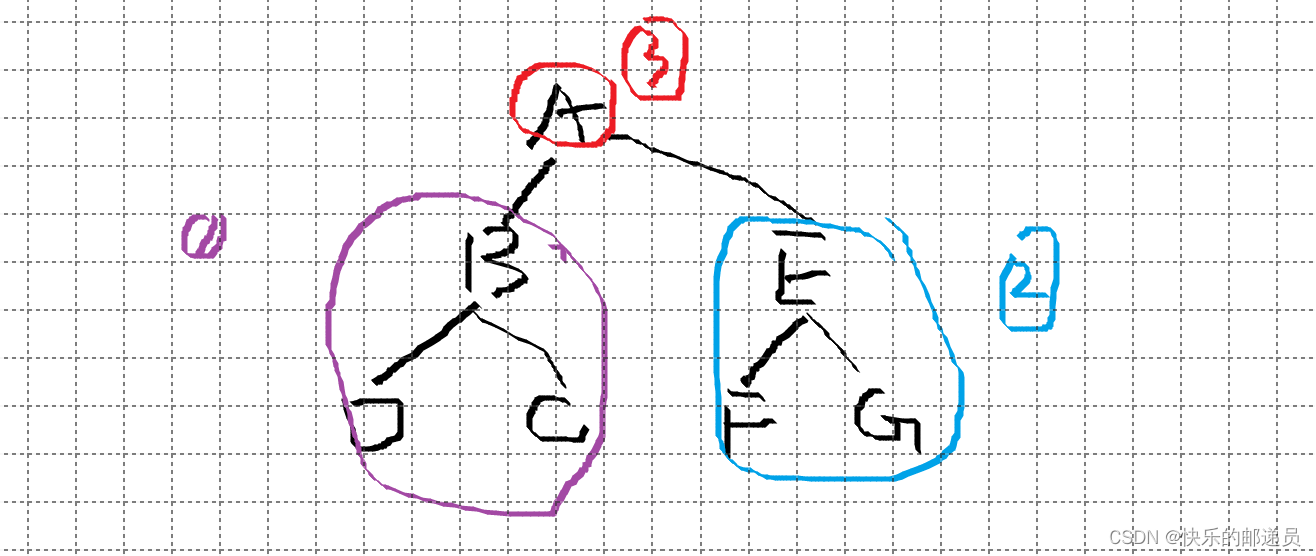
后序遍历:DCB? FGE A?
10.?若将一棵树?T?转化为对应的二叉树?BT,则下列对?BT?的遍历中,其遍历序列与?T?的后根遍历序列相同的是:(B)
A.先序遍历
B.中序遍历
C.后序遍历
D.按层遍历?
11.按照二叉树的定义,具有3个结点的二叉树有几种?(C)
A.3
B.4
C.5
D.6
12.二叉树中第5层(根的层号为1)上的结点个数最多为:(C)
A.8
B.15
C.16
D.32
第i层上的结点个数最多为2^(i-1)
13.?先序遍历图示二叉树的结果为(B)

A.A,B,C,D,H,E,I,F,G
B.A,B,D,H,I,E,C,F,G
C.H,D,I,B,E,A,F,C,G
D.H,I,D,B,E,F,G,A,C
14.对?n?个互不相同的符号进行哈夫曼编码。若生成的哈夫曼树共有 115 个结点,则?n?的值是:(C)
A.56
B.57
C.58
D.60
2n-1=115 2n=116 n=58
哈夫曼树只有度为0和度为2的结点,这里的n为度为0的结点数量
15.?数据结构在计算机内存中的表示是指(A )。
A数据的存储结构
B.数据结构
C.数据的逻辑结构
D.数据元素之间的关系
数据结构在计算机内存中表示是指数据的存储结构(物理结构)
16.?在存储数据时,通常不仅要存储各数据元素的值,而且还要存储(C )。
A.数据的处理方法
B.数据元素的类型
C.数据元素之间的关系
D.数据的存储方法
在存储数据时,通常不仅要存储各数据元素的值,还要存储数据元素之间的关系
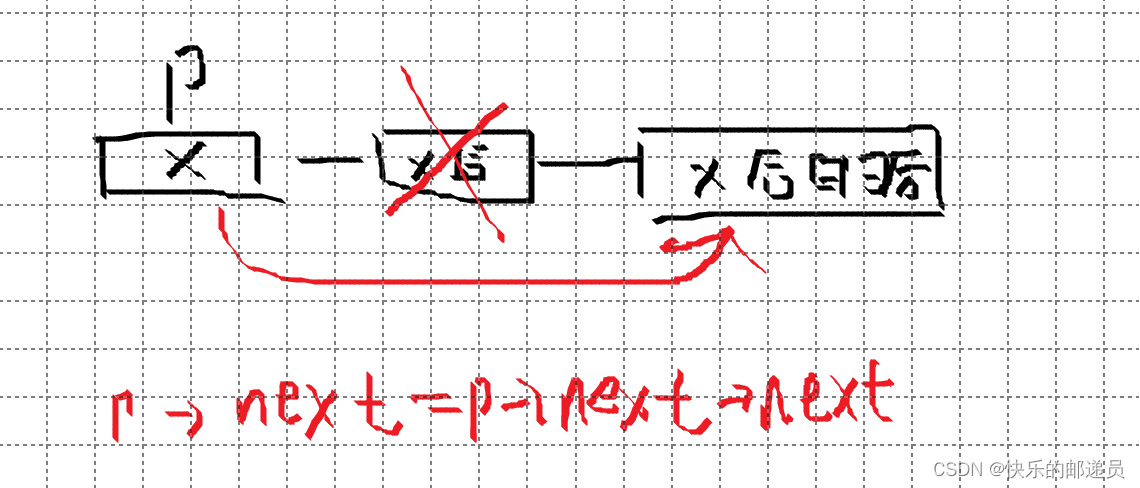
?17.在单链表中,指针p指向元素为x的结点,实现“删除x的后继”的语句是(B)。
A.p=p->next
B.p->next=p->next->next
C.p->next=p
D.p=p->next->next
18.?对一个具有n个元素的线性表,建立其单链表的时间复杂度为(A)。
A.O(n)
B.O(1)
C.O(n2)
D.O(log2?n)
创建一个包含n个结点的单链表的时间复杂度为o(n)
创建一个包含n个结点的有序单链表的时间复杂度是O(n2)。??
建立一个有序的单链表,则每生成一个新结点时需要和已有的结点进行比较,时间复杂度为O(n),所以确定合适的插入位置的单链表,时间复杂度是O(n^2)。
19.?有关树和二叉树的叙述错误的是(C)。
A.树中的最大度数没有限制,而二叉树结点的最大度数为2;
B.树的结点无左右之分,而二叉树的结点有左右之分;
C.树的每个结点的孩子数为0到多个, 而二叉树每个结点均有两个孩子;
D.树和二叉树均为树形结
二叉树的结点可以小于等于2
20.?某线性表采用顺序存储结构,每个元素占4个存储单元,首地址为100,则第12个元素的存储地址为(A)。
A.144
B.145
C.147
D.148
100+11*4=144
21.?在下列存储形式中,( D)不是树的存储形式。
A.双亲表示法
B.孩子链表表示法
C.孩子兄弟表示法
D.顺序存储表示法
树的存储形式:孩子链表表示法、孩子兄弟表示法、双亲表示法
22.?二叉树的高度
若根节点为高度1,一棵具有 1025 个结点的二叉树的高度为 ▁▁▁C▁▁ 。
A.10
B.11
C11~1025 之间
D.10~1024 之间
[log2(1025)]+1=10+1=11
23.?栈和队列的共同点是____。(C)
A.都是先进后出
B.都是先进先出
C.只允许在端点处插入和删除元素
D.没有其冋点
24.为解决计算机主机与打印机之间速度不匹配问题,通常设置一个打印数据缓冲区,主机将要输出的数据依次写入该缓冲区,而打印机则依次从该缓冲区中取出数据。该缓冲区的逻辑结构应该是?(B)
A.堆栈
B.队列
C.树
D.图
25.下列与队列结构有关联的是(D)
A.函数的递归调用
B.数组元素的引用
C.多重循环的执行
D.先到先服务的作业调度
队列先进先出的特点,队列的修改依据先进先出的原则
26.?与数据元素本身的形式、内容、相对位置、个数无关的是数据的( C)。
A.存储结构
B.存储实现
C.逻辑结构
D.运算实现
与数据元素本身的形式、内容、相对位置、个数无关的是数据的逻辑结构
27.?数据结构中,与所使用的计算机无关的是数据的( A) 结构。
A.逻辑
B.存储
C.逻辑和存储
D.物理
28.某线性表中最常用的操作是在最后一个元素之后插入一个元素和删除第一个元素,则采用什么存储方式最节省运算时间?(B)
A.单链表
B.仅有尾指针的单循环链表
C.仅有头指针的单循环链表
D.双链表
在最后一个元素之后插入一个元素或者删除一个第一个元素,采用仅有尾指针的单循环链表
29.?若某表最常用的操作是在最后一个结点之后插入一个结点或删除最后一个结点。则采用哪种存储方式最节省运算时间?(D)
A.单链表
B.双链表
C.单循环链表
D.带头结点的双循环链表
在最后一个结点之后插入一个结点或者删除最后一个结点,采用带头结点的双循环链表
30.?如果二叉树的前序遍历结果是12345,后序遍历结果是32541,那么该二叉树的中序遍历结果是什么?(D)
A.23145
B.23154
C.24135
D.无法确定
前序+后序无法确定一个二叉树
31.要使一棵非空二叉树的先序序列与中序序列相同,其所有非叶结点须满足的条件是(B):
A.只有左子树
B.只有右子树
C.结点的度均为1
D.结点的度均为2
32.采用链结构存储线性表时,其地址(B )。
A.必须是连续的
B.连续不连续都可以
C.部分地址必须是连续
D.必须是不连续的
采用链式存储结构存储线性表,其地址连不连续都可以。
33.?下面描述中正确的为( C)。
A.线性表的逻辑顺序与物理顺序总是一致的。
B.线性表的顺序存储表示优于链式存储表示。
C.线性表若采用链式存储表示时所有结点之间的存储单元地址可连续可不连续。
D.二维数组是其数组元素为线性表的线性表。
A.若线性表采用链式存储,则不一定一致
B.在不同的情况下,优缺点不同
D.二维数组是数据元素为一维数组的线性表(数组元素改为数据元素)
34.?对N(N≥2)个权值均不相同的字符构造哈夫曼树。下列关于该哈夫曼树的叙述中,错误的是:(D)
A.树中一定没有度为1的结点
B.树中两个权值最小的结点一定是兄弟结点
C.树中任一非叶结点的权值一定不小于下一层任一结点的权值
D.该树一定是一棵完全二叉树
A.哈夫曼树中,只有度为0的点和度为2的点
B.哈夫曼树并不一定是满二叉树
C因为哈弗曼树的构造每一次选择两个权值最小的节点,来形成哈弗曼树的第一个新节点,
,哈弗曼树的构造思想就是贪心的思想,自底向上建树,因此对于一棵哈弗曼树来说,树中任一非叶节点的权值一定不小于下一层的任意节点的权值。D.哈夫曼树并不一定满足完全二叉树的定义
完全二叉树:
1叶子结点只可能出现在最后两层
2.度为1的结点个数为0或1
满二叉树一定是完全二叉树,完全二叉树不一定是满二叉树
35.?哈夫曼树是n个带权叶子结点构成的所有二叉树中(C)最小的二叉树。
A.权值
B.高度
C.带权路径长度
D.度
36.数组A[1..5,1..6]每个元素占5个单元,将其按行优先次序存储在起始地址为1000的连续的内存单元中,则元素A[5,5]的地址为:(C)
A.1120
B.1125
C.1140
D.1145
按行序:1000+(4*6+4)*5=1140
37.若某线性表最常用的操作是存取任一指定序号的元素和在最后进行插入和删除运算,则利用哪种存储方式最节省时间?(D)
A.双链表
B.单循环链表
C.带头结点的双循环链表
D.顺序表
存取任一指定序号的元素和在最后进行插入和删除运算,采用顺序表最好
38.?设一个栈的输入序列是1、2、3、4、5,则下列序列中,是栈的合法输出序列的是?(A)
A.3 2 1 5 4
B.5 1 2 3 4
C.4 5 1 3 2
D.4 3 1 2 5
栈:先进后出
A.1进2进3进 3出 2出1出 4进 5进 5出 4出? 3 2 1 5 4
B1进2进3进4进5进 5出 4出 3出2出1 出 5 4 3 2 1
C1进 2进 3进 4进 4出5进 5出 3出 2 出 1出? ?4 5 3 2 1
D1进 2进 3进 4进 4出 3出 2出1出 5进 5出? ?4 3 2 1 5
39.?有六个元素以6、5、4、3、2、1的顺序进栈,问哪个不是合法的出栈序列?(B)
A.2 3 4 1 5 6
B.3 4 6 5 2 1
C.5 4 3 6 1 2
D.4 5 3 1 2 6
6比5先进,6比5后出,B不符合
40.?(neuDS)若将整数1、2、3、4依次进栈,则不可能得到的出栈序列是( D)。
A.1234
B.1324
C.4321
D.1423
2比3先进,2比3后出
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- Git常用命令及解释说明
- IPO:血透圈“进口”当道,国产威高血净能否成“全村希望”?
- 【算法题】32. 最长有效括号
- 实战:Python+微信公众号,轻松实现固定格式的消息定向推送
- Python3.6+selenium实现操作Frame中的页面元素
- 天文观测与计算机技术:粉丝的视角
- 我的创作纪念日
- 邦芒忠告:写个人简历时千万不要犯十个错误
- logback日志记录器
- 网安零基础超全学习路线,认真学好,1周入门,3月即可精通