Python实现基于广义线性回归模型进行Meta分析(meta_analysis算法)项目实战

说明：这是一个机器学习实战项目（附带数据+代码+文档+视频讲解），如需数据+代码+文档+视频讲解可以直接到文章最后获取。

1.项目背景

对于广义线性回归模型在Meta分析中的应用概念，可能是将其用于处理非正态分布或非线性关系的数据，例如：

1.当原始研究的结果数据不是连续型且服从正态分布，而是二项分布（如成功率）、泊松分布（如发病率）或其他分布时，可以通过GLM设定适当的链接函数和分布族来适应。

2.在进行Meta回归分析时（探讨效应量与潜在协变量之间的关系），如果效应量与协变量的关系并非线性，也可以利用GLM的灵活性引入非线性变换。

本项目通过GLM算法来构建广义线性回归模型进行Meta分析。??

2.数据获取

本次建模数据来源于网络(本项目撰写人整理而成)，数据项统计如下：

编号	变量名称	描述
1	e2i
2	nei
3	c2i
4	nci

数据详情如下(部分展示)：

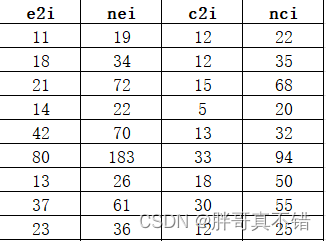
3.数据预处理

3.1?用Pandas工具查看数据

使用Pandas工具的head()方法查看前五行数据：

关键代码：

3.2 数据缺失查看

使用Pandas工具的info()方法查看数据信息：

从上图可以看到，总共有4个变量，数据中无缺失值，共17条数据。

关键代码：

3.3?数据描述性统计

通过Pandas工具的describe()方法来查看数据的平均值、标准差、最小值、分位数、最大值。

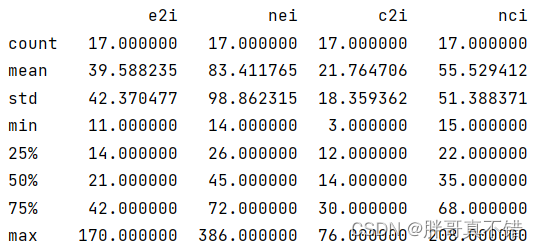
关键代码如下：

4.探索性数据分析

4.1?变量直方图

用Matplotlib工具的hist()方法绘制直方图：

从上图可以看到，变量主要集中在25~125之间。

4.2 相关性分析

?????

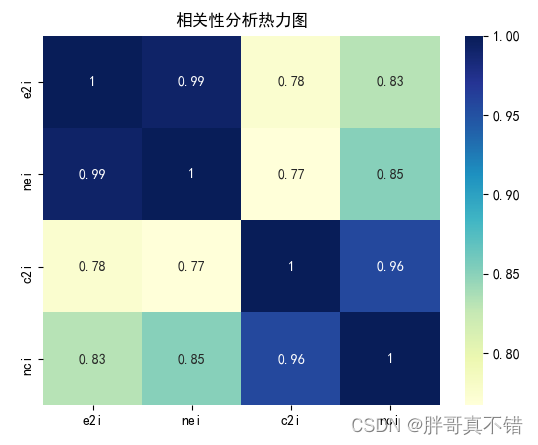从上图中可以看到，数值越大相关性越强，正值是正相关、负值是负相关。

4.3 进行二项分布比例的Meta分析一

输出所使用的随机效应模型方法及估算得到的τ2值：

汇总表的具体内容：

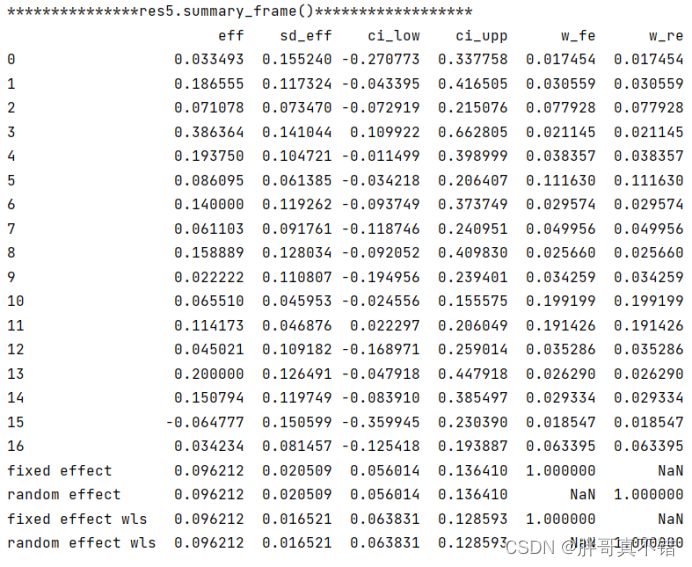
4.4 进行二项分布比例的Meta分析二

更改数据以具有正随机效应方差，进行Meta分析。

输出所使用的随机效应模型方法：

4.5 进行二项分布比例的Meta分析三

输出所使用的随机效应模型方法：

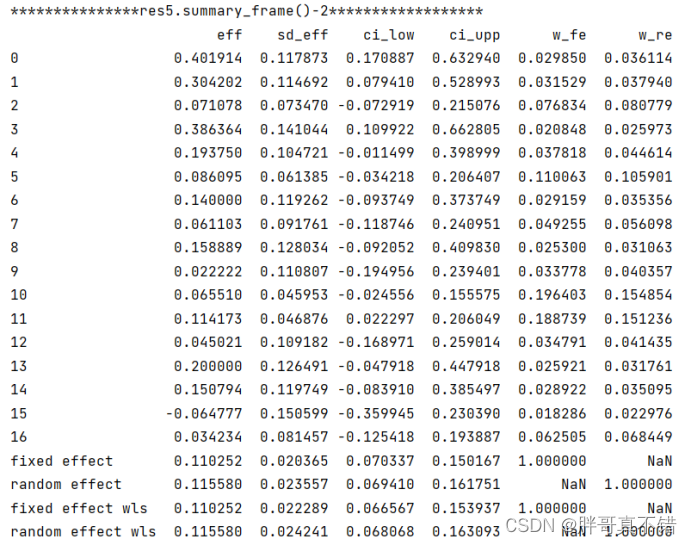
4.6 进行二项分布比例的Meta分析四

所使用的效应量统计量类型为比值比。

5.构建GLM模型

主要使用GLM算法，用于目标回归进行Meta分析。

5.1 构建模型

编号	模型名称	参数
1	GLM模型	var_weights=weights?

5.2?模型摘要信息一

设置了scale参数为1。scale参数通常用于指定残差的尺度。

尺度参数（scale）及计算结果：

5.3?模型摘要信息二

参数scale，这里的值设为 "x2"，表示采用了一个特定的尺度估计方法。

尺度参数（scale）及计算结果：

# 本次机器学习项目实战所需的资料，项目资源如下：
 
# 项目说明：
 
# 获取方式一：
 
# 项目实战合集导航：
 
https://docs.qq.com/sheet/DTVd0Y2NNQUlWcmd6?tab=BB08J2
 
# 获取方式二：

链接：https://pan.baidu.com/s/1lgrNNLLPIzZXl2CdNZYvDQ 
提取码：yzzl