离散数学知识点-期末复习

目录

一、利用真值表求主析取范式、主合取范式

1.例题

二、推理证明

1.推理规则

2.例题?

三、符号化命题

四、有穷集的计数

1.包含互斥原理?

2.例题

?1.文氏图法?

2.包含互斥原理法

五、关系的闭包

1.三种闭包

2.Warshall算法

3.例题

六、等价关系

1.定义

2.例题?

七、最小生成树的应用题

---

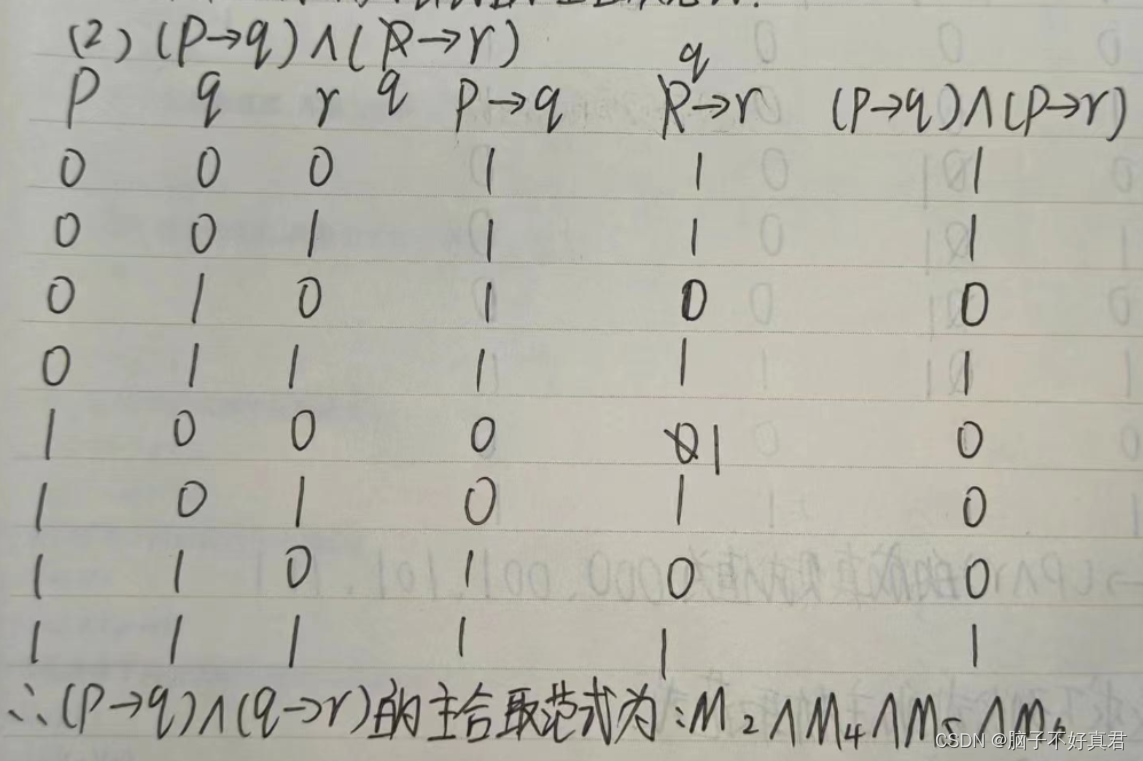
一、利用真值表求主析取范式、主合取范式

? 用真值表求出公式的成真赋值和成假赋值，主析取范式：成真赋值用m一一析取组合；主合取范式：成假赋值用M一一合取组合

1.例题

二、推理证明

1.推理规则

2.例题?

三、符号化命题

四、有穷集的计数

1.包含互斥原理?

2.例题

1.文氏图法?

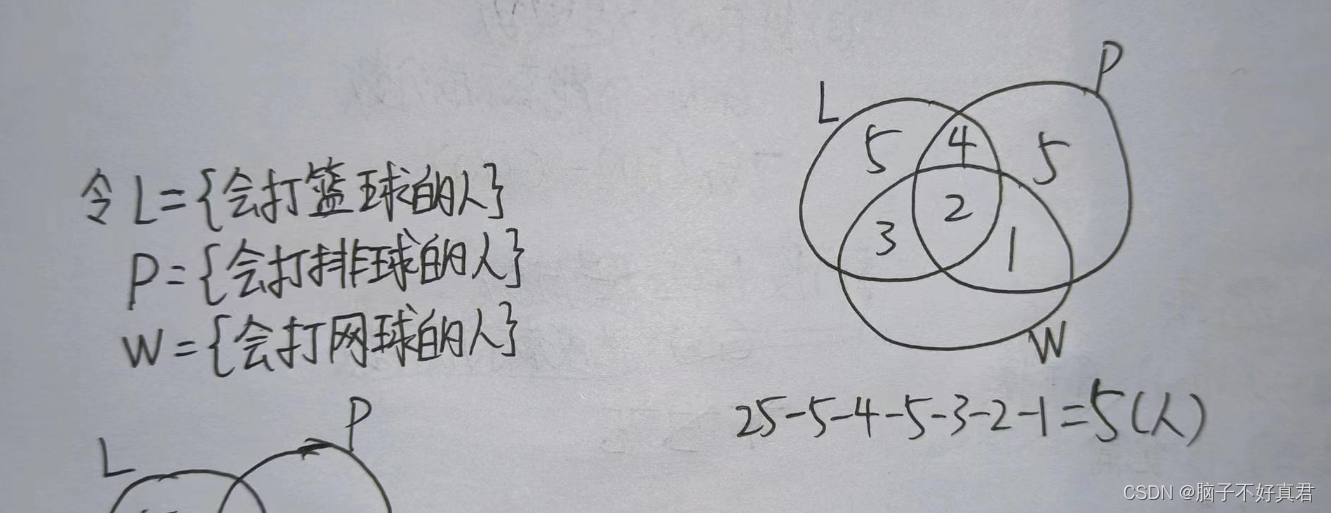
2.包含互斥原理法

五、关系的闭包

1.三种闭包

如果R = {1,2,3}，那么R的恒等关系 = {<1,1><2,2><3,3>}

如果R = {<2,3><4,1><6,7>}，那么R^-1 = {<3,2><1,4><7,6>}

2.Warshall算法

设M(R的关系矩阵)

当i=1时，看第1列为1的元素所在的行，将第一行加到这些行。

当i=2时，看第2列为1的元素所在的行，将第二行加到这些行。

当i=3时，看第3列为1的元素所在的行，将第三行加到这些行。

当i=4时，看第4列为1的元素所在的行，将第四行加到这些行。

上述加为逻辑加，如下，可以用真(1)假(0)析取来理解：
0+0=0， 0∨0=0
0+1=1， 0∨1=1
1+0=1， 1∨0=1
1+1=1， 1∨1=1

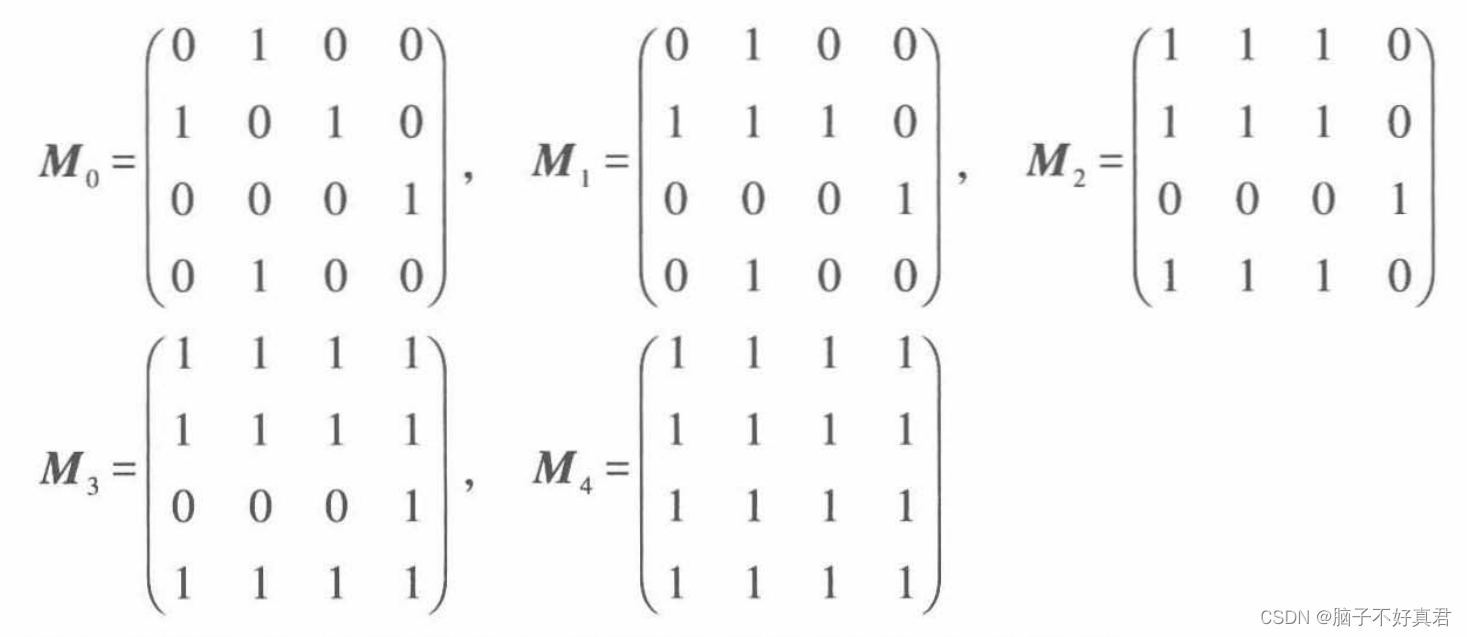
3.例题

六、等价关系

1.定义

也就是说，R在A上满足自反性、对称性、传递性。

2.例题?

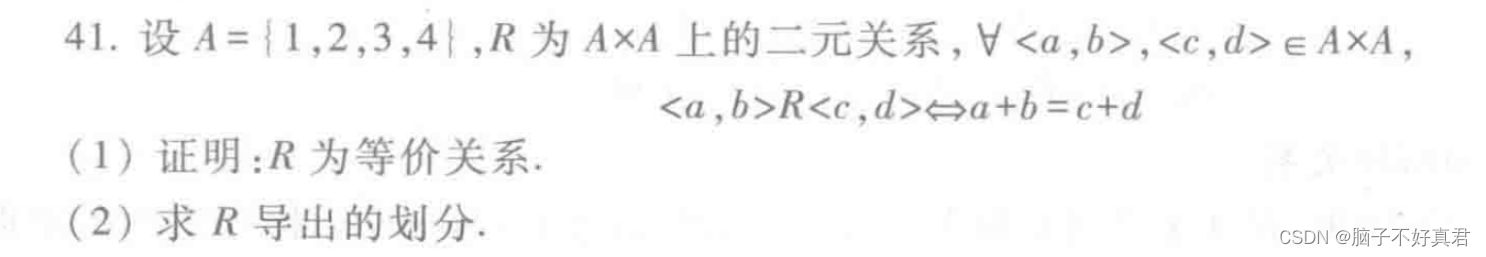
七、最小生成树的应用题

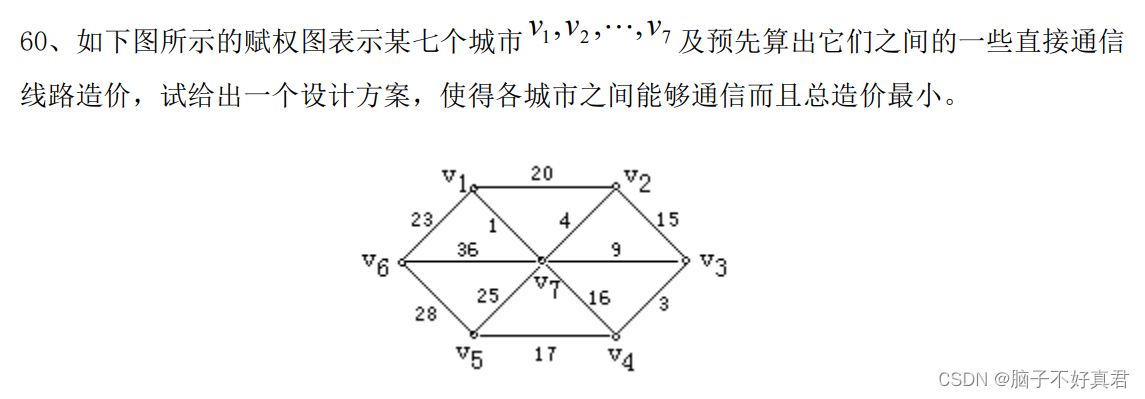
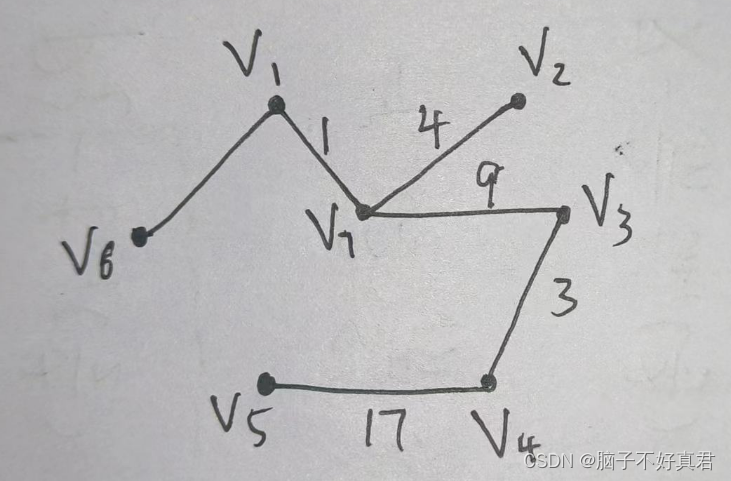
最小生成树画法：每次取权值最小的边，并且不构成回路，直到画出所有顶点。?