概率论与数理统计————古典概型、几何概型和条件概率

发布时间：2024年01月15日

一、古典概型

特点

（1）有限性：试验S的样本空间的有限集合

（2） 等可能性：每个样本点发生的概率是相等的

公式：P（A）=\frac{A}{S}???????? A为随机事件的样本点数；S是样本空间

二、几何概型

计算公式：p（A）=\frac{A}{S}???? A的长度、面积或体积????? S的长度、面积或体积

三、条件概率

条件概率：设A、B为两个事件，且p（B）>0,则在事件B条件下事件A发生的概率为

P（A|B）=\frac{P(AB)}{P(B)}

p（\bar{B}|A）=1-P（B|A）

乘法公式：

四、全概率公式和贝叶斯公式

完备事件组：（1）A1、A2、A3、.....、An两两互斥?? （2）A1\cup A2\cup A3\cup .....\cup An=S

则称A1A2A3An为完备事件组，或者一个划分

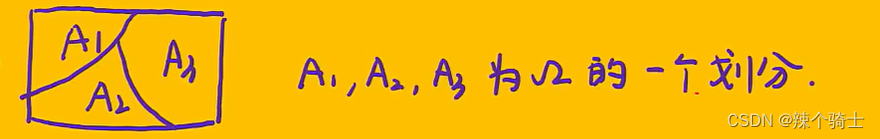
全概率公式：设B事件为任意事件，A1、A2、A3、.......、An为完备事件组

P（B）=P（A1)P(B|A1)+P(A2)P(B|A2)+,,,,,,,,,+P(An）P（B|An）

贝叶斯公式：设B事件为任意事件，A1、A2、A3、.......、An为完备事件组

P（Ai|B）=\frac{AiB}{B}=\frac{p(Ai)P(B|Ai)}{\sum P(Ai)P(B|Ai)}

文章来源:https://blog.csdn.net/2201_75333727/article/details/135601054
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。
最新文章