算法训练-力扣.435无重叠区间(贪心)

#435无重叠区间. - 力扣（LeetCode）

这道题算是很经典的一道贪心类型的题

题目描述

给定一个区间的集合?intervals?，其中?intervals[i] = [starti, endi]?。返回?需要移除区间的最小数量，使剩余区间互不重叠?。

示例 1:

输入: intervals = [[1,2],[2,3],[3,4],[1,3]]
输出: 1
解释: 移除 [1,3] 后，剩下的区间没有重叠。

示例 2:

输入: intervals = [ [1,2], [1,2], [1,2] ]
输出: 2
解释: 你需要移除两个 [1,2] 来使剩下的区间没有重叠。

示例 3:

输入: intervals = [ [1,2], [2,3] ]
输出: 0
解释: 你不需要移除任何区间，因为它们已经是无重叠的了。

提示:

• 1 <= intervals.length <=
• intervals[i].length == 2
• -5 * ?<= starti?< endi?<= 5 *

解题

思路

读完这道题，我脑海中就浮现了一个横向坐标轴，上面画着每个区间：

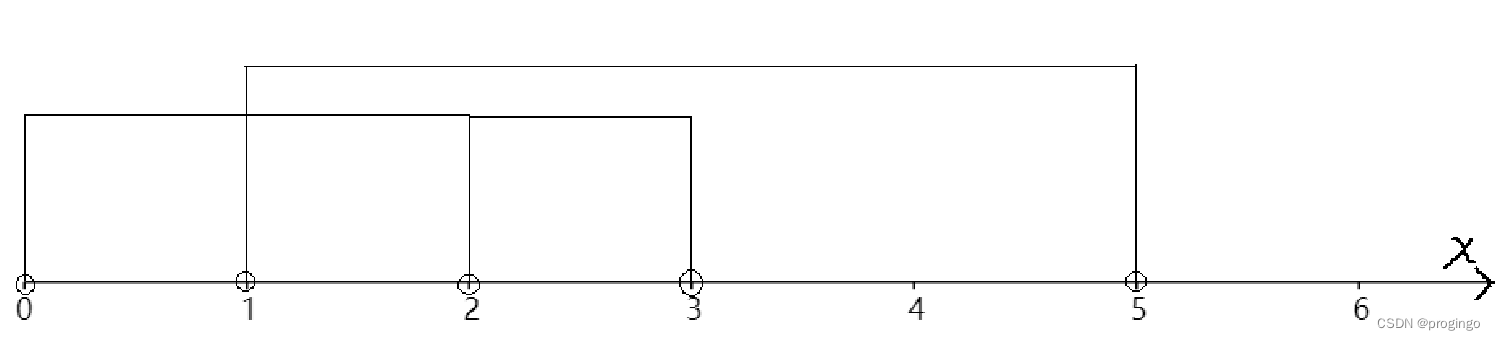
题目让我们求移除区间的最少数量，那意思也就是我们要尽可能保留多的区间，那这不就很像往箱子里放物品，求怎样放能放下最多的物品吗？那这时候我们肯定要将物品从小到大排个序，先放小的物品，再放大的物品，这样以此能放下最多的物品（如下图）。我们将坐标轴看成箱子，区间看成物品，那这题不就迎刃而解了吗？

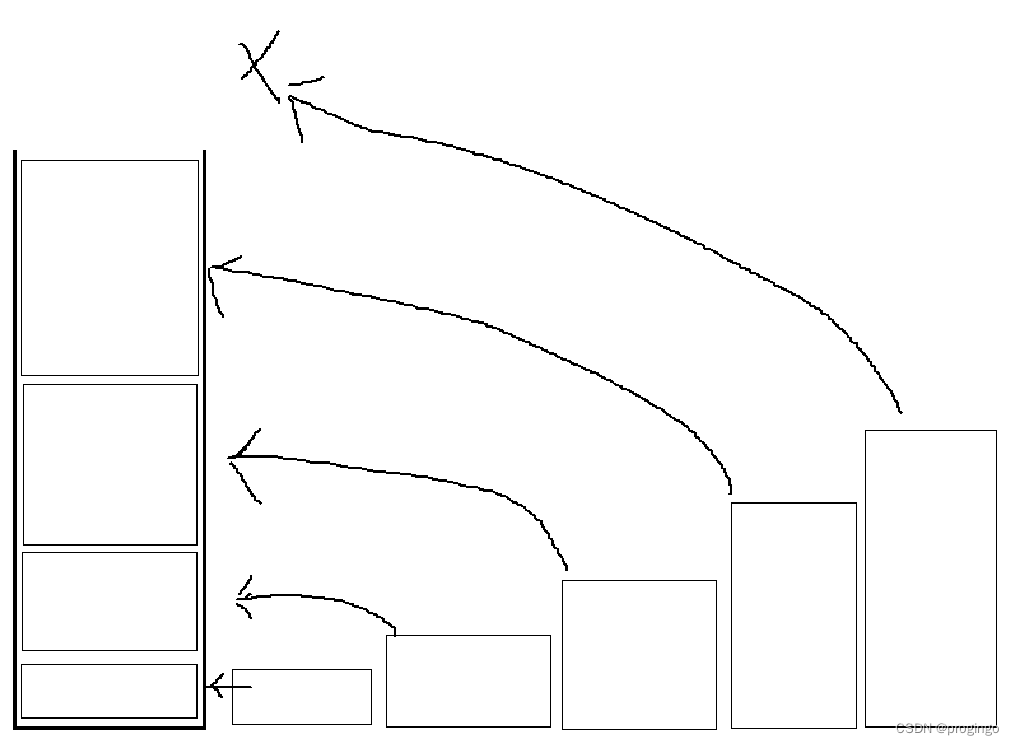
那现在我就应该先将数组里的区间进行一个排序。这时候问题来了，应该按照什么规则来排？

错误思路

我最初的思路是优先按照区间的左坐标从小到大排，如果左坐标相同，则按照区间长度，也就是右坐标减去左坐标的大小来排。排完序后，就遍历数组，如果发现有重叠的区间就抛弃。

想象总是美好的，现实总是残酷的。按照这种排序规则咋一看没什么问题，三个测试用例也都能通过。但是也很容易举出一个反例：[?[2,3] , [3,4] , [1,4] ]。正常答案其实是1，去掉[1,4]即可，但是如果用上面这种方法，那么返回的结果是2 (去掉的是[2,3] , [3,4]这两个区间)。显然这不是我们想要的答案，那应该怎么排序呢？

正确思路

①其实上面以放物品的角度来思考问题是完全没问题的。只不过是排序的规则出错了，正确的做法应该以每个区间的右坐标，从小到大来排序。原因也很简单，还是用放物品的角度来思考问题，我们之所以要先选小的物品放进去是因为小物品他的高更矮，取决于下一个物品的位置因素是上一个物品的高，放到这个问题里，取决于下一个区间的起始坐标取决于上一个区间的结束坐标，比如第一个区间为[1 , 2]，那么下一个元素的起始坐标必须大于等于2。结合题目，我们要放下尽可能多的区块，所以就要优先放结束坐标小的区块，这也就是为什么我们要按照区块的结束坐标endi进行排序，这也是这道题贪心的所在！

②为了能顺利解出这道题，我们需要用一个变量 right 来维护已存放区块的最大结束坐标。比如当前已经放了区块[1,2][3,5][5,8]那么right就等于8，下一个区块的起始坐标必须要大于right，这就是right的作用。

③将数组中的区块都排好序后，我们只需要遍历数组中的区块，发现已经被覆盖的元素抛弃掉并记录，若发现当前区块是没有被覆盖的，就保留并更新right。

根据上面的三个步骤，不难得出代码：

public static int eraseOverlapIntervals(int[][] intervals) {
    Arrays.sort(intervals, (o1, o2) -> o1[1] - o2[1]);//将intervals中的元素item按照item[1]的大小进行排序

    int right = intervals[0][1];//维护已存放的区块的最右坐标
    int res = 0;
    for (int i = 1;i < intervals.length;++i){
        if (intervals[i][0] < right){
            //当前区块的左坐标小于right，抛弃
            res++;
        }else {
            //不会被覆盖，可以放入该区块，并更新right
            right = intervals[i][1];
        }
    }
    return res;
}

很愉快，又AC了一道经典题。