归并排序和快速排序的相关运用

1.归并排序

归并排序是一个时间复杂度为O(N*logN)的排序算法，算法的原理不难，但是它在排序时的性质，会衍生出一些问题的特定解法。

1.1小和问题

在一个数组中，每一个数左边比当前数小的数累加起来，叫做这个数组的小和。求一个数组 的小和。例如:[1,3,4,2,5] 1左边比1小的数，没有; 3左边比3小的数，1；4左边比4小的数，1、3； 2左边比2小的数，1； 5左边比5小的数，1、3、4、2；所以小和为1+1+3+1+1+3+4+2=16

那我们常规的暴力写法就是枚举每个数，看看前面有多少比它小的数，最后累加起来。这个方法的时间复杂度肯定是O(N²)。我们不妨换一个思路来看待这个问题，下面看这个图。
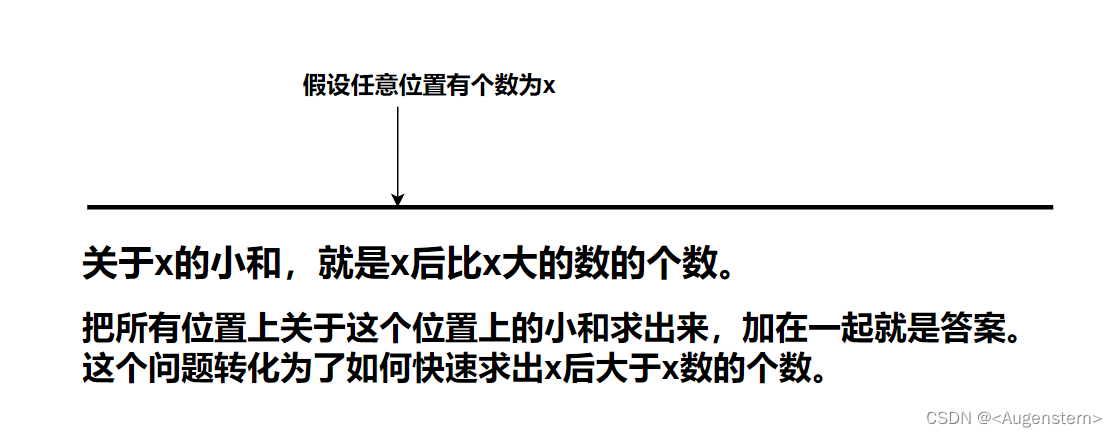可以利用归并排序的排序信息，这样去统计。
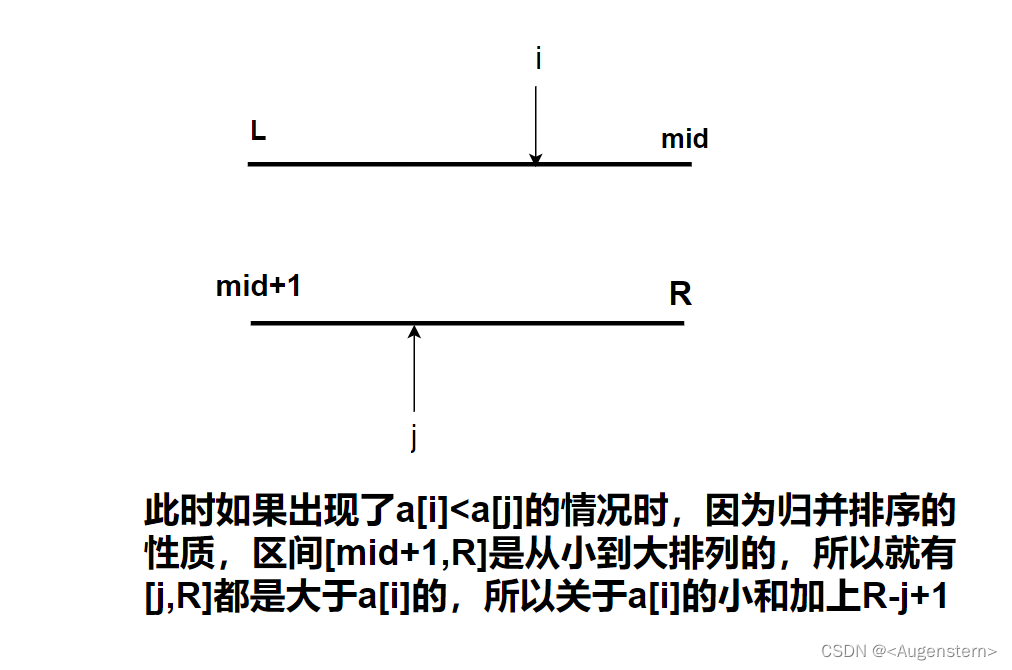由归并排序的过程，这样统计出来的小和个数一定是不重不漏的。
下面是代码

#include <iostream>
#include <vector>
using namespace std;
class Solution{
public:
    int merge(vector<int>&arr, int L, int mid, int R)
    {
    int p1 = L;
    int p2 = mid + 1;
    vector<int> help(R - L + 1);
    int res = 0;
    int i = 0;                      //i为help数组下标
    while (p1 <= mid && p2 <= R) {
        res += arr[p1] < arr[p2] ? arr[p1] * (R - p2 + 1) : 0;
        help[i++] = arr[p1] < arr[p2] ? arr[p1++] : arr[p2++];
    }
    while (p1 <= mid) {
        help[i++] = arr[p1++];
    }
    while (p2 <= R) {
        help[i++] = arr[p2++];
    }
    for (int i = 0; i < help.size(); i++) {
        arr[L + i] = help[i];
    }
    return res;
    }

    int mergeSort(vector<int>&arr, int L, int R) {
    if (L == R) {
        return 0;
    }
    int mid = L + ((R - L) >> 1);
    return mergeSort(arr, L, mid) + mergeSort(arr, mid + 1, R) + merge(arr, L, mid, R);
    }
    

    int smallSum(vector<int>&arr) 
    {
    if (arr.size() < 2) 
        return 0;
        
    return mergeSort(arr, 0, arr.size()-1);
    
    }

};

1.2逆序对问题

给定一个长度为 n的整数数列，请你计算数列中的逆序对的数量。

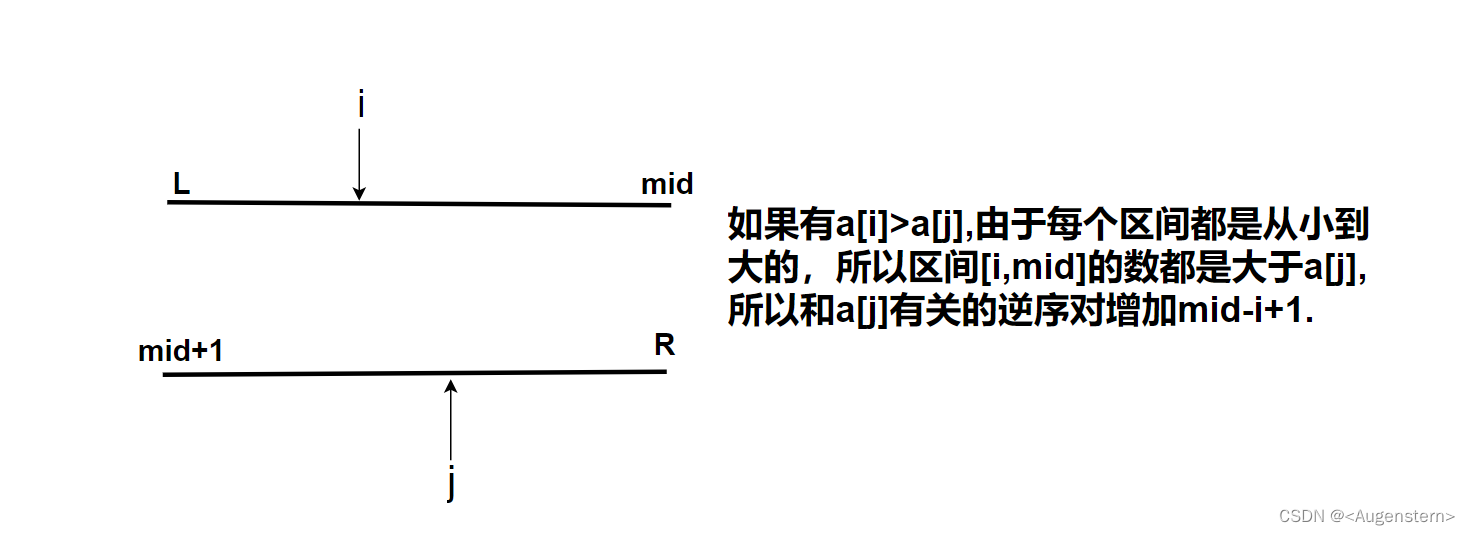
逆序对的定义如下：对于数列的第 i个和第 j 个元素，如果满足 i<j且 a[i]>a[j]，则其为一个逆序对；否则不是。

这个题的思路和上个题是一样的，我们看下面这个图
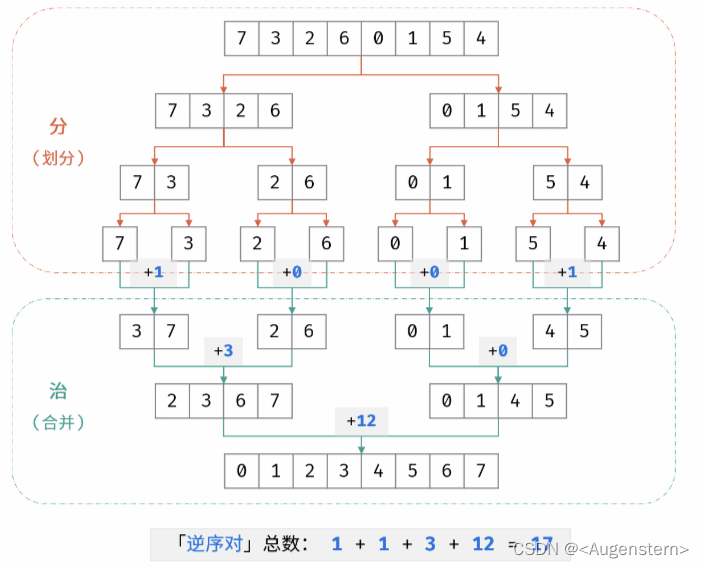
这里找了一张比较好理解的过程图

下面是代码

class Solution {
public:
    int reversePairs(vector<int>& record) {
        vector<int> tmp(record.size());
        return mergeSort(0, record.size() - 1, record, tmp);
    }
    
    int mergeSort(int l, int r, vector<int>& record, vector<int>& tmp) {
        // 终止条件
        if (l >= r) return 0;
        // 递归划分
        int m = (l + r) / 2;
        int res = mergeSort(l, m, record, tmp) + mergeSort(m + 1, r, record, tmp);
        // 合并阶段
        int i = l, j = m + 1;
        for (int k = l; k <= r; k++)
            tmp[k] = record[k];
        for (int k = l; k <= r; k++) {
            if (i == m + 1)
                record[k] = tmp[j++];
            else if (j == r + 1 || tmp[i] <= tmp[j])
                record[k] = tmp[i++];
            else {
                record[k] = tmp[j++];
                res += m - i + 1; // 统计逆序对
            }
        }
        return res;
    }
};

2.快速排序

2.1荷兰国旗问题

荷兰国旗问题，让我们把所有小于x的数放在左边，所有等于x的数放中间，大于x的数放右边。如何去操作呢？
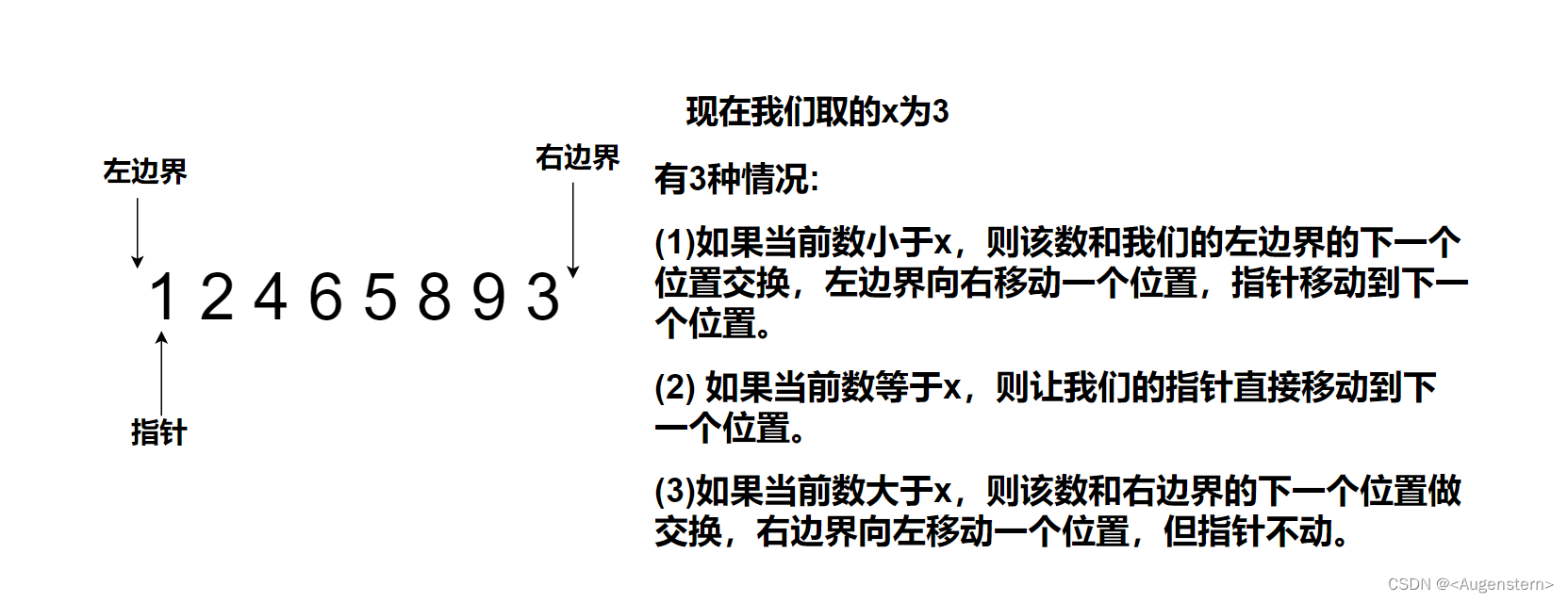下面来模拟过程

一开始定好左右边界：

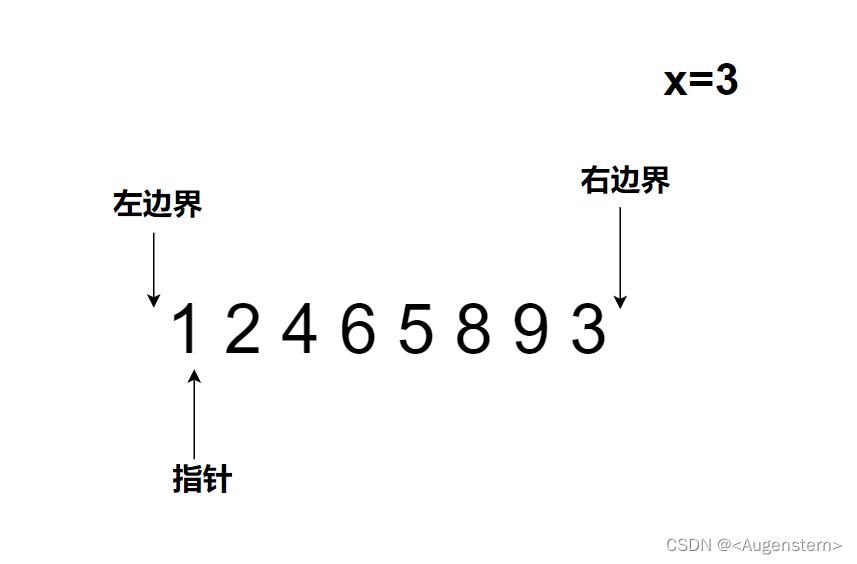
因为1<3所以属于情况(1)

2<3，继续重复(1)操作
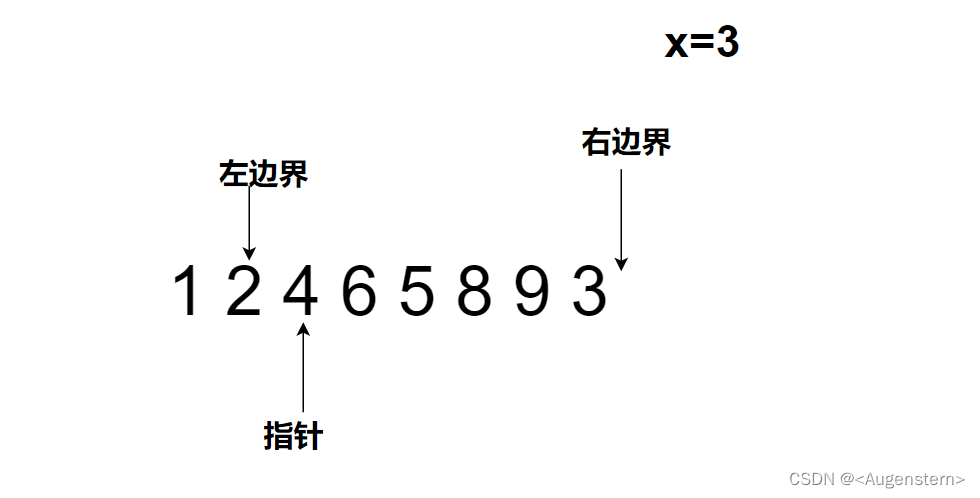4>3，进行(3)操作
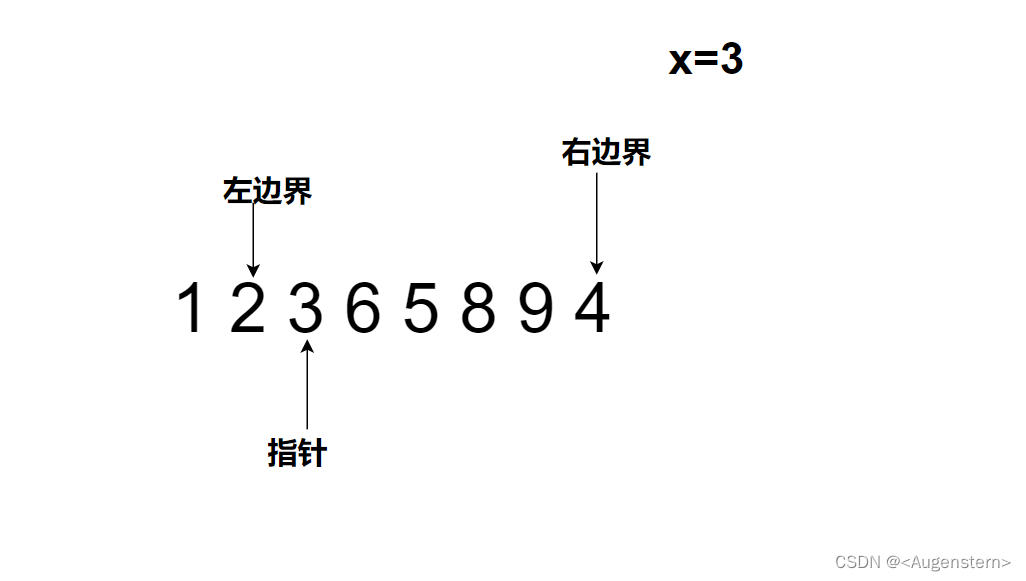3=3，进行(2)操作

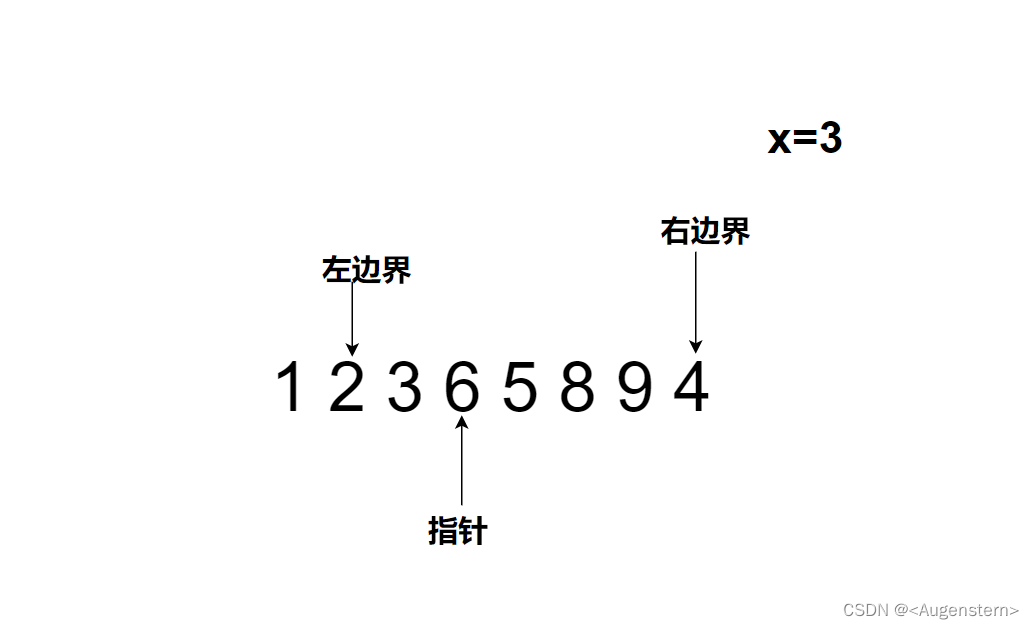6>3，进行操作(3）

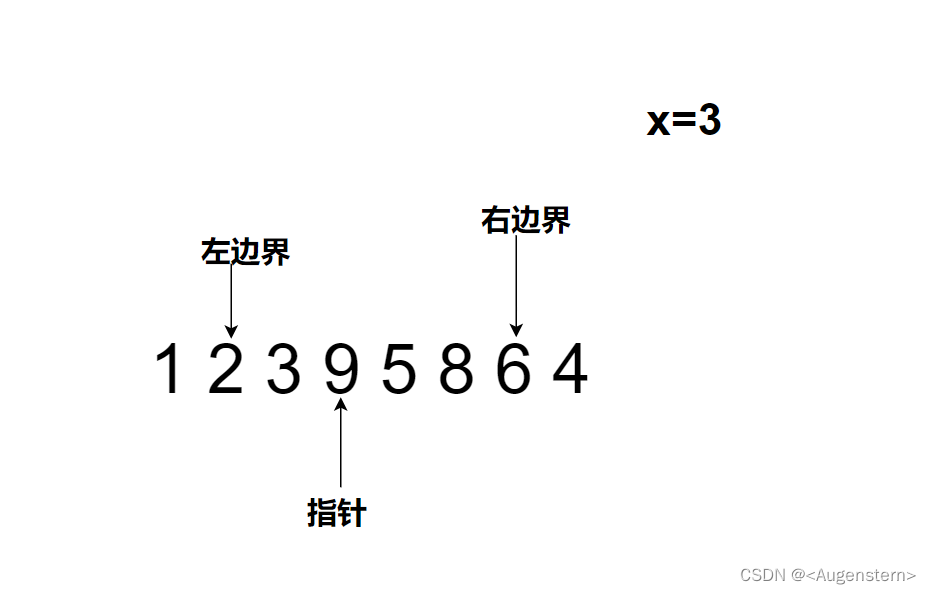
9>3进行(3)操作

8>3进行(3)操作

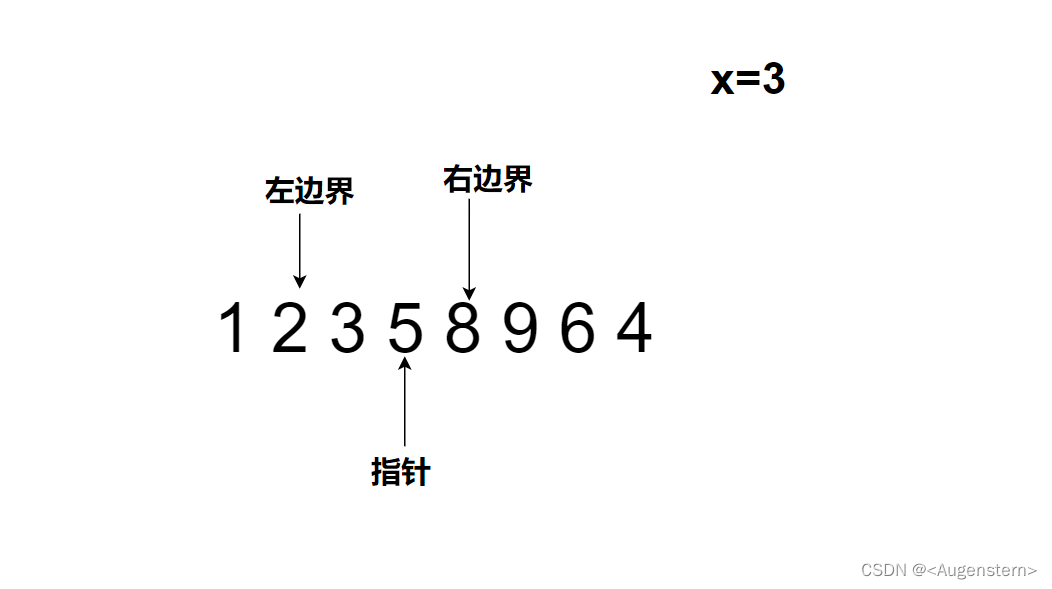5>3，进行(3)操作
最后指针和右边界重合，停止循环。

最后我们划分出了三块位置：
[L，左边界]为小于x；[左边界+1，右边界-1]为等于x；[右边界，R]为大于x。

我们下面就可以通过这样的划分写出快排了，因为等于x的区间已经排好，现在分别处理小于x的和等于x的就可以了。这相对与传统双指针快排更快，因为我们一次排好了所有和x相等所有数，而双指针每次只排好一个数。 下面看代码：

//荷兰国旗问题
pair<int, int> getflag(vector<int>&arr, int L, int R)
{
    if (L > R)
    {
        return { -1,-1 };
    }
    if (L == R) return { L,R };
    int less = L - 1;
    int more = R;
    int idx =L;
    //每次选取x=arr[R]进行划分。
    while (idx < more)
    {
        if (arr[idx] == arr[R]) idx++;
        else if (arr[idx] < arr[R])
            swap(arr[++less], arr[idx++]);
        else if (arr[idx] > arr[R])
            swap(arr[--more], arr[idx]);
    }
    swap(arr[R], arr[more]);
    return { less + 1,more };
}


void process(vector<int>& arr, int L, int R)
{
    if (L >= R) return;

    pair<int, int> tmp = getflag(arr, L, R);
    //tmp存放x的左右边界。
    process(arr, L, tmp.first - 1);
    process(arr, tmp.second + 1, R);
}
void quick_sort(vector<int>& arr)
{
    if (arr.size() < 2) return;
    process(arr, 0, arr.size() - 1);
}

2.2随机快速排序

我们发现如果每次都选择最后一个数的话，会出现最差的情况，如果该数组是从小到大排好序的，这样操作的时间复杂度为O(N²)。所以我们因该随机取数，使这个区间中的每个数，取到它的概率都相等，最后数学家通过计算期望，发现这个时间复杂度收敛于O(N*logN)，下面是代码。

#include <iostream>
#include <algorithm>
#include <vector>
using namespace std;

//荷兰国旗问题
pair<int, int> getflag(vector<int>&arr, int L, int R)
{
    if (L > R)
    {
        return { -1,-1 };
    }
    if (L == R) return { L,R };
    int less = L - 1;
    int more = R;
    int idx =L;

    //随机取数x=arr[m];
    int m = rand() % (R - L + 1) + L;


    //把它与arr[R]交换
    swap(arr[m], arr[R]);


    while (idx < more)
    {
        if (arr[idx] == arr[R]) idx++;
        else if (arr[idx] < arr[R])
            swap(arr[++less], arr[idx++]);
        else if (arr[idx] > arr[R])
            swap(arr[--more], arr[idx]);
    }
    swap(arr[R], arr[more]);
    return { less + 1,more };
}
void process(vector<int>& arr, int L, int R)
{
    if (L >= R) return;

    pair<int, int> tmp = getflag(arr, L, R);
    //tmp为等于x的左右边界。
    process(arr, L, tmp.first - 1);
    process(arr, tmp.second + 1, R);
}
void quick_sort(vector<int>& arr)
{
    if (arr.size() < 2) return;
    process(arr, 0, arr.size() - 1);
}

int main()
{
    vector<int> arr{ 1,3,2,4 };
    quick_sort(arr);
    for (int i = 0; i < arr.size(); i++)
        cout << arr[i];
    return 0;

}

2.3非递归的随机快速排序

这个就是我们自己用栈，去记录每次处理左右边界。下面是代码

#include <iostream>
#include <algorithm>
#include <vector>
#include <stack>
using namespace std;

//荷兰国旗问题
pair<int, int> getflag(vector<int>& arr, int L, int R)
{
    if (L > R)
    {
        return { -1,-1 };
    }

    if (L == R) return { L,R };
    int less = L - 1;
    int more = R;
    int idx = L;

    //随机取数x=arr[m];
    int m = rand() % (R - L + 1) + L;


    //把它与arr[R]交换
    swap(arr[m], arr[R]);


    while (idx < more)
    {
        if (arr[idx] == arr[R]) idx++;
        else if (arr[idx] < arr[R])
            swap(arr[++less], arr[idx++]);
        else if (arr[idx] > arr[R])
            swap(arr[--more], arr[idx]);
    }
    swap(arr[R], arr[more]);
    return { less + 1,more };
}


void quick_sort(vector<int>& arr)
{
    if (arr.size() < 2) return;

    //分为两个区间
    pair<int, int> tmp = getflag(arr, 0, arr.size()-1);
    stack<pair<int, int>> st;

    int l = tmp.first;
    int r = tmp.second;

    st.push({ 0,l - 1 });
    st.push({ r + 1,arr.size() - 1 });
    
    //继续划分区间，并用栈记录
    while (!st.empty())
    {
        pair<int, int> t = st.top();
        st.pop();

        int l = t.first, r = t.second;

         //如果区间有多个数,继续处理
        if (l < r)
        {
            pair<int, int> tmp = getflag(arr, l, r);

            int pl = tmp.first;
            int pr = tmp.second;
            st.push({ l,pl - 1 });
            st.push({ pr + 1,r });
        }
    }

}