力扣：977. 有序数组的平方59. 螺旋矩阵 II

给你一个按?非递减顺序?排序的整数数组?nums，返回?每个数字的平方?组成的新数组，要求也按?非递减顺序?排序。

这题关键是非递减关键字，含义就是可能有相等的数，也有可能是负数；

思路1：先把所有的数都转换成正整数->排序->排序后进行平方,具体代码实现如下：

var sortedSquares = function(nums) {
  for(let i = 0; i < nums.length;i++){
      nums[i] = Math.abs(nums[i])
  }
  nums.sort((a,b)=>a-b);
  for(let i = 0; i < nums.length;i++){
      nums[i] = nums[i]*nums[i]
  }
  return nums;
};

用了两个for循环，一个sort，时间复杂度是O(n)+O(n)+O(n*logn);即时间复杂度是O(n*logn);

思路2：通过总结归纳发现不管有没有负数还是都是正数，两头的平方总是比中间的数要大，如下示意图：

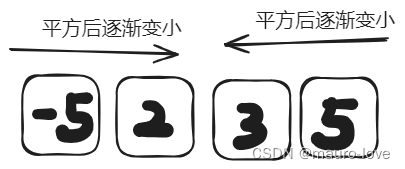
通过双指针的方法，从两边向中间收拢的方法，比较两边平方之后的数，较大的放到目标数组中，放入数组的下标向中间靠拢（即，left大即left++，right大即right--);具体代码实现如下：

var sortedSquares = function(nums) {
  let left = 0;
  let right = nums.length -1;
  const result = []
  for(left,right;left<=right;){
      const resLeft = nums[left]*nums[left];
      const resRight = nums[right]*nums[right]
      if(resLeft >= resRight){
          result.unshift(resLeft);
          left++
      } else {
          result.unshift(resRight);
          right--;
      }
  }
  return result;
};

在力扣上跑，是通过了，但是排名靠后，是什么原因呢？仔细分析是因为使用了unshift方法，导致每插入一个数，数组都要重新排列；因为每次数组的下标对应的数值都在改变，也就是每次unshift后面所有的数都要更新一次，很好性能；

找到问题就优化一下，具体代码如下：

var sortedSquares = function(nums) {
  let left = 0;
  let right = nums.length -1;
  const result = new Array(right);
  let resIndex = right;
  for(left,right;left<=right;){
      const resLeft = nums[left]*nums[left];
      const resRight = nums[right]*nums[right]
      if(resLeft >= resRight){
          result[resIndex] = resLeft
          left++
      } else {
          result[resIndex] = resRight
          right--;
      }
      resIndex--;
  }
  return result;
};

到这里用双指针的方法实现了这个时间复杂度为O(n)的方法；

59. 螺旋矩阵 II：给你一个正整数?n?，生成一个包含?1?到?n2?所有元素，且元素按顺时针顺序螺旋排列的?n x n?正方形矩阵?matrix?。

按照左到右，上到下，右到左，下到上的顺序一圈一圈填数的思路，具体代码如下：

var generateMatrix = function(n) {
    let q = 0;  // 转动圈数
    let num = 1; // 填充的数字
    let i = 0; // 二维数组列index；
    let j = 0; // 二维数组行index；
    const sql = n*n; // 平方数最大值，作为终止条件对比数
    const result = [] // 存放结果
    while(num <=sql){
        if(!result[j]) result[j] = []; // 如果行是空的就创建一个数组
        for(i;i <=n -1- q&& num <= sql;i++){ // 从左至右存放行数据；
            result[j][i] = num++;
        }
        i--; // 因为自增多了需要自减
        for(j++;j <=n -1- q&& num <= sql;j++){ // 从上至下存放行数据；
            if(!result[j]) result[j] = [];
            result[j][i] = num++;
        }
        j--;
        for(i--;i>=0+q&& num <= sql;i--){ // 从右至左存放行数据；
            result[j][i] = num++;
        }
        i++;
        for(j--;j>=1+q&& num <= sql;j--){// 从下至上存放行数据；
            result[j][i] = num++;
        }
        j++; // 内圈需要自增1行
        i++; // 内圈需要自增1列
        q++; // 圈数增加1
    }
    return result;
};

事已至此还是先吃饭吧！