直流电机闭环调速实验
?直流电机闭环调速实验
直流电机闭环调速系统是一个典型的按偏差调节的闭环控制系统,通过系统的调节,使电机的转速与期望的给定速度一致。
本次实验我们就以AEDK-LabACT 自控/计控原理实验箱中的直流电机为对象,分析讨论直流电机闭环调速系统设计中涉及到的系统辨识、控制算法仿真及实现等内容。
- 实验目的
通过本次实验,我们可以达到以下目的:
- 了解直流电动机速度闭环控制随动系统的组成和工作原理。
- 了解和掌握连续控制系统的 PID 控制算法的模拟表达式(微分方程)。
- 掌握速度控制随动系统对象的数学模型实验辩识,并写出其传递函数。
- 了解和掌握数字 PID 调节器控制参数的工程整定方法。
- 了解和掌握用 MATLAB 数字 PID 仿真被控过程。
- 了解和掌握用 LabACT 实验箱数字 PID 实验被控过程。
- 观察和分析在标准 PID 控制系统中,P.I.D 参数对系统性能的影响。
二、实验原理及说明
本实验系统由AEDK-LabACT 自控/计控原理实验箱中的电机和电机驱动功率放大器、调节器、电机转速检测传感器、F/V 转换器等组成,组成框图见图 2-1。

该系统是一个按偏差调节的闭环控制系统。被控对象是直流电机,给定值为电机速度值(以脉冲或电压形式),输出量为电机实际速度值。
工作过程为:
当给定直流电机转速 U(R)接入后,与当前转速值 U(t)(测速输出)相比较,其差值e(t)在计算机中进行 PID 计算,解算成u(t),经数/模转换器(B2)驱动直流电机,改变电机转速,达到直流电机闭环调速控制。
系统实现直流电机的闭环调速系统由模/数转换器(B7)、微型计算机、数/摸转换器(B2)和直流电机模块(C2)(包括电机测速)组成。
其中电机采用了 BY25?直流电机。
电机测速是由直流电机带动光栅盘转动,光栅盘上有 12 个透光孔,光栅盘下有一个光电断续器,它输出一组频率正比于电机转速的脉冲信号,经过一级 74LS14 滤去毛刺后送至该模块中的 F/V 转换,通过 F/V 转换就可以得到表征电机的当前转速的电压值。
采用ADC0809作为模/数转换器,实现将输入的模拟量转换为8bit 数字输出。其中“IN4 和 IN5”测孔为 0~+5V 模拟量输入,“IN6 和 IN7”测孔为-5V~+5V 模拟量输入。电机转速的电压值从IN4输入后转换为8位数字量,并在计算机中与给定速度对应的数字量进行偏差计算。
在计算机中根据控制算法计算出控制量,再将控制量转换为模拟量输出。
系统采用 DAC0832 作为数/摸转换器,可实现 8bit 数字输入转换为模拟量。数字 0~0FFH 输入,
经数/模转换后 OUT1?测孔输出为 0~+5v?模拟量。改变数/摸转换输入值,就可以控制直流电机的转速。
电机驱动功率放大器输入/输出电压范围:0~+5V,电机转速传感器检测F/V 转换器输出电压范围:0~+5V,对应于电机转速为 0~3300 转/分。控制算法采用PID控制。
按偏差的比例、积分、微分控制(简称 PID 控制)是过程控制中应用最广的一种控制规则。由 PID 控制规则构成的 PID 调节器是一种线性调节器。这种调节器是将设定值 R?与实际输出值 Y 构成控制偏差:e=R-Y,按偏差的比例(P)、积分(I)、微分(D)通过线性组合构成控制量。
PID 控制算法的模拟表达式是:
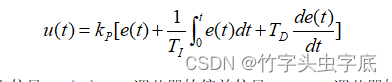
式中, u(t )——调节器的输出信号;e(t )——调节器的偏差信号; KP——调节器的比例系数;TI ——调节器的积分时间常数; TD ——调节器的微分时间常数。
在实际应用中,根据对象特征和控制要求,也可灵活改变其结构,取其一部分构成控制,例如:比例(P)调节器、比例积分(PI)调节器、比例微分调节器(PD)等。
用数字形式的差分方程来代替连续系统的微分方程:

式中:T——采样周期;u(k)——第 k?次采样时计算机输出;e(k)——第 k?次采样时的偏差值;
e(k-1)——第?k-1次采样时的偏差值;k——采样序号,k=0,1,2,…。
离散化的 PID 控制算式表达式为:

式中: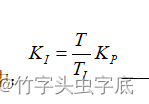
——积分系数;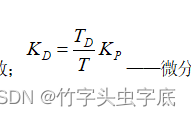
——微分系数。
三.实验内容及步骤
(一)速度控制随动系统对象的数学模型实验辩识及建立
本实验采用实际的电机和电机驱动功率放大器、调节器、电机转速检测传感器、F/V 转换器等组成的速度控制随动系统作为实验被控对象,这就有必要对该随动系统的数学模型进行实验测定和辩识。
1.调整频率/电压(F/V)转换静态工作点
B1 单元中电位器的左边 K3 开关拨下(GND),右边 K4 开关拨上(+5V),信号输出(B1 的 Y 测孔)调整为+3V(调节方法:调节电位器,用万用表测量 Y 测孔)。Y 测孔联线到 C2?模块电机输入测孔, 调整 C2?模块中的电位器 W2,使电机输出电压测孔上的直流电压等于+3V。
2.电机模型实验辩识
实验辩识构成见图 2-2,0→+3V?阶跃电压同时加到电机驱动功率放大器输入及二个惯性环节串联组成的模拟电路输入端。

图 2-2 ?速度控制随动系统对象的数学模型实验测定和辩识构成
系统辨识实验步骤:
- 在显示与功能选择(D1)单元中,通过波形选择按键选中‘矩形波’(矩形波指示灯亮)。
- 量程选择开关 S2 置下档,调节“设定电位器 1”,使之矩形波宽度≥1 秒(D1 单元左显示)。
- 调节 B5 单元的“矩形波调幅”电位器使矩形波输出电压= 3V(D1 单元右显示)。
???????????4)构造模拟电路:按图 2-2?安置短路套及测孔联线,接线表如下:

5)运行、观察、记录:此时示波器选×1 档
将函数发生器(B5)单元‘矩形波’输出(OUT)作为信号发生器,施加于系统的输入端 Ui,
?先运行 LABACT?程序,选择界面的“工具”菜单选中“双迹示波器”项,点击开始,用虚拟示波器观察模拟被控对象所测得的响应曲线与实际的被控对象的输出响应曲线,见图 2-3。
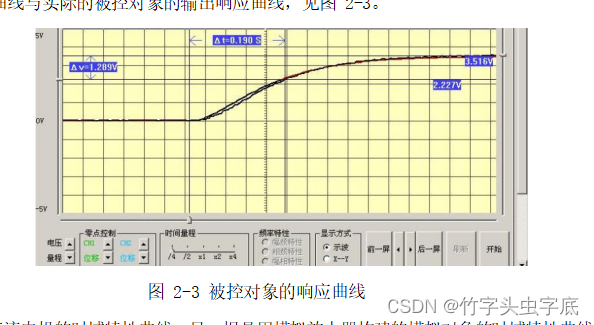
图 2-3?被控对象的响应曲线
图 2-3?中一根是直流电机的时域特性曲线,另一根是用模拟放大器构建的模拟对象的时域特性曲线。
6)若两根曲线不一致,则调整模拟放大器的结构参数,直至模拟被控对象所测得的响应曲线与实际的被控对象的响应曲线十分接近为止。
图中绿色线是直流电机时域特性曲线,蓝色是模拟放大器构建的模拟对象时域特性曲线。可见,两跟曲线在初始值及稳态值基本重合,增益相同,而动态过程不同。
调整模拟对象参数的原则是保证增益不变的情况下,增加或减少模拟对象的时间常数,减缓或加快模拟对象响应速度。
为简便起见,我们只调整A5单元的参数。用A11单元(阻容元件库)的两个可变电阻分别取代A5单元的输入电阻和反馈电阻。此时应将短路套S3和S12取下,增加测孔连线A5H1——A11可变电阻1(上),A5IN——A11可变电阻1(下);A5IN——A11可变电阻2(上);A5OUT——A11可变电阻2(下)。在调节可变电阻值时要求两个可变电阻的阻值保持一致以达到改变时间常数而增益不变的目的。
7)由直流电机和用模拟放大器构建的模拟对象的时域特性曲线相比对,由模拟被控对象仿真出直流电机的模型参数构成。
由图2-2,模拟对象由两个惯性环节串联构成。
第一个环节:增益K1=100K/100K=1,时间常数T1=100K*1u=0.1s;
第二个环节:增益K2=20K/20K=1,时间常数T1=20K*3u=0.06s。即得T1=0.1S,T2=0.06S K=1。
列出被控对象的传递函数为:
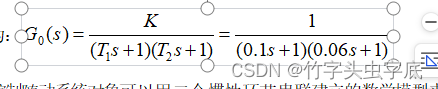
8)实验结果表明,电机速度控制随动系统对象可以用二个惯性环节串联建立的数学模型来近似,其传递函数为:

??(2-1)
这是典型的自平衡双容被控过程,在工程中普遍采用“有时延的单容被控过程”来近似:?????
![]() ???????
???????
???????????(2-2)
在被控对象响应曲线图中,测量输出电压的稳态值Y(∞),并求出该值的30%及70%对应的时间,分别记为t1,t2,如图2-4、图2-5所示.
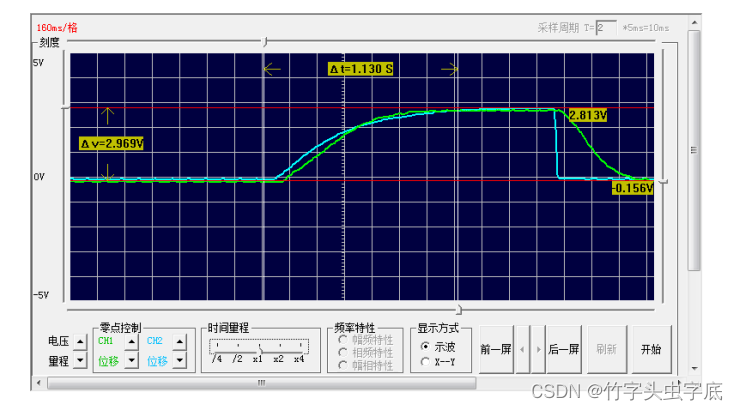
图2-4 求Y(∞)
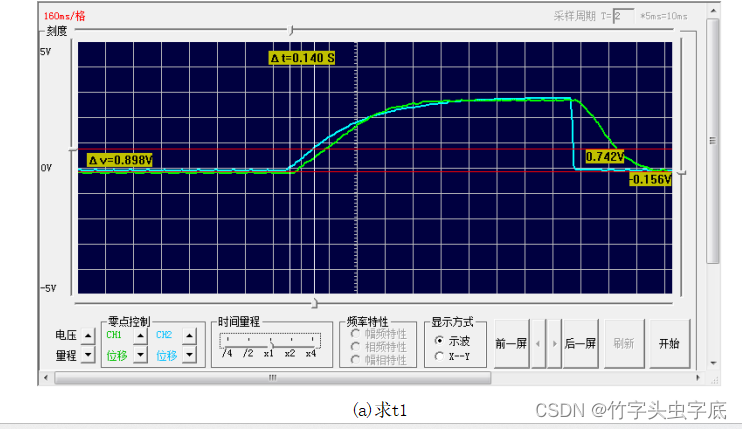
- 求t1
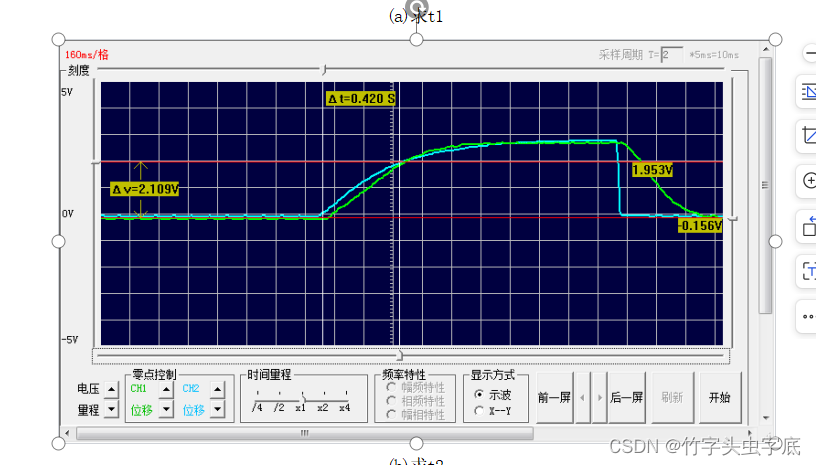
- 求t2
图?2-5 求t1及t2
下面以图2-3的对象的响应曲线为例讨论
从实验响应曲线图中可测得t1=0.086S;测得t2=0.192S;
由式(2-3)计算,其被控对象的参数。
??(2-3
根据式(2-3)计算,其被控对象的参数为:
,
???????????????????????
(二)采样周期的选择
如果采样周期T与被控对象的时间常数能符合下式,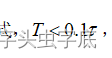
,则将可获得良好的 PID 调节效果。
选采样周期T为4mS。
(三)数字 PID 调节器控制参数的工程整定方法
数字 PID 控制参数的工程整定方法为开环整定法—反应曲线法(动态特性参数法)。
????????????????????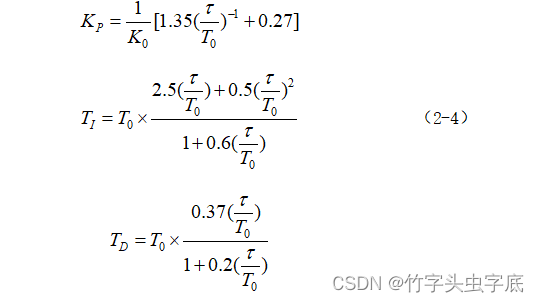
?????????????(2-4)
由式(2-3)计算,得其被控对象的参数:T0=0.125 S ,τ=0.042 S。选采样周期 T 为 4mS。代入式(2-4)求得数字 PID 调节器控制参数:KP=4.35、TI=0.092、TD=0.0144。
在maltab中,输入如下程序段,即可自动求出时间常数T、纯滞后时间τ、采样周期、PID参数。
clear all;
close all;
clc;
sys=tf(1,conv([0.1 1],[0.06 1])); ?%模拟电路仿真模型
r=3; ????????????????????%阶跃值
[y,t]=step(sys); ????%单位阶跃响应,y为单位阶跃输出,t为对应的时间点
yout=r*y;
%以下求t1和t2时间值
yt1=0.3*yout(end); ???????????%0.3yout(无穷)
yt2=0.7*yout(end); ???????????%0.7yout(无穷)
indt1=find(yout>=yt1); ????%找到输出序列中大于0.3yout无穷的所有序号 ?
%第一个序号即为刚刚大于0.3yout无穷,找到其对应时间,即为t1
t1=t(indt1(1)) ??????????????????
indt2=find(yout>=yt2);%找到输出序列中大于0.7yout无穷的所有序号 ?
%第一个序号即为刚刚大于0.7yout无穷,找到其对应时间,即为t2
t2=t(indt2(1))
%下面求带纯滞后一阶系统模型
k0=yout(end)/r ??????????????????%开环增益
T0=(t2-t1)/0.8467 ?????????????????????????%惯性时间
tao=(t1*1.204-t2*0.3567)/0.8467 ??????%纯滞后时间
%系统辨识后,求PID参数
T=0.1*tao ?????????????????????????%采样周期
alpha=tao/T0;
Kp=(1.35/alpha+0.27)/k0 ???%比例系数
Ti=T0*(2.5*alpha+0.5*alpha*alpha)/(1+0.6*alpha) %积分时间常数
Td=T0*0.37*alpha/(1+0.2*alpha) ???????%微分时间常数
Ki1=T/Ti
Kd1=Td/T
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 推挽输出、开漏输出、上拉输入、下拉输入、浮空输入。
- C语言每日一题(47)两数相加II
- 2023.12.31每日一题
- 【Spring Boot 3】【Redis】消息发布及订阅
- Notepad++ v7.7.1 安装及添加插件
- Java在线学习网站(源码+开题)
- 【LeetCode】202. 快乐数(简单)——代码随想录算法训练营Day06
- java: 5-3 for
- ubuntu卸载docker
- 酒精壁炉,现代取暖的便携选择