算法训练营Day19

#Java #二叉树 #双指针

开源学习资料

Feeling and experiences：

二叉搜索树的最小绝对差：力扣题目链接

给你一个二叉搜索树的根节点 root ，返回 树中任意两不同节点值之间的最小差值 。

差值是一个正数，其数值等于两值之差的绝对值。

之前递归搜索树写多了，导致首先想到的方法 是把每个节点与左右子树值的差返回给上一级作比较。

但是该题目更好的做法是用中序遍历：

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    int minNode; //记录答案
    int pre; //用来记录前一个节点
    public int getMinimumDifference(TreeNode root) {
    //初始化最大值
    minNode = Integer.MAX_VALUE;
    //初始化为-1；
    pre = -1;
    dfs(root);
    return minNode;
    }

    public void dfs(TreeNode node){
        if(node == null){
            return;
        }
        //利用中序遍历
        //先遍历左子树
        dfs(node.left);
        //用pre记录前一个节点的值
        if(pre == -1){
            pre = node.val;
        }else{
            minNode = Math.min(minNode , node.val - pre);
            pre = node.val;
        }
        //遍历右子树
        dfs(node.right);
    }
}

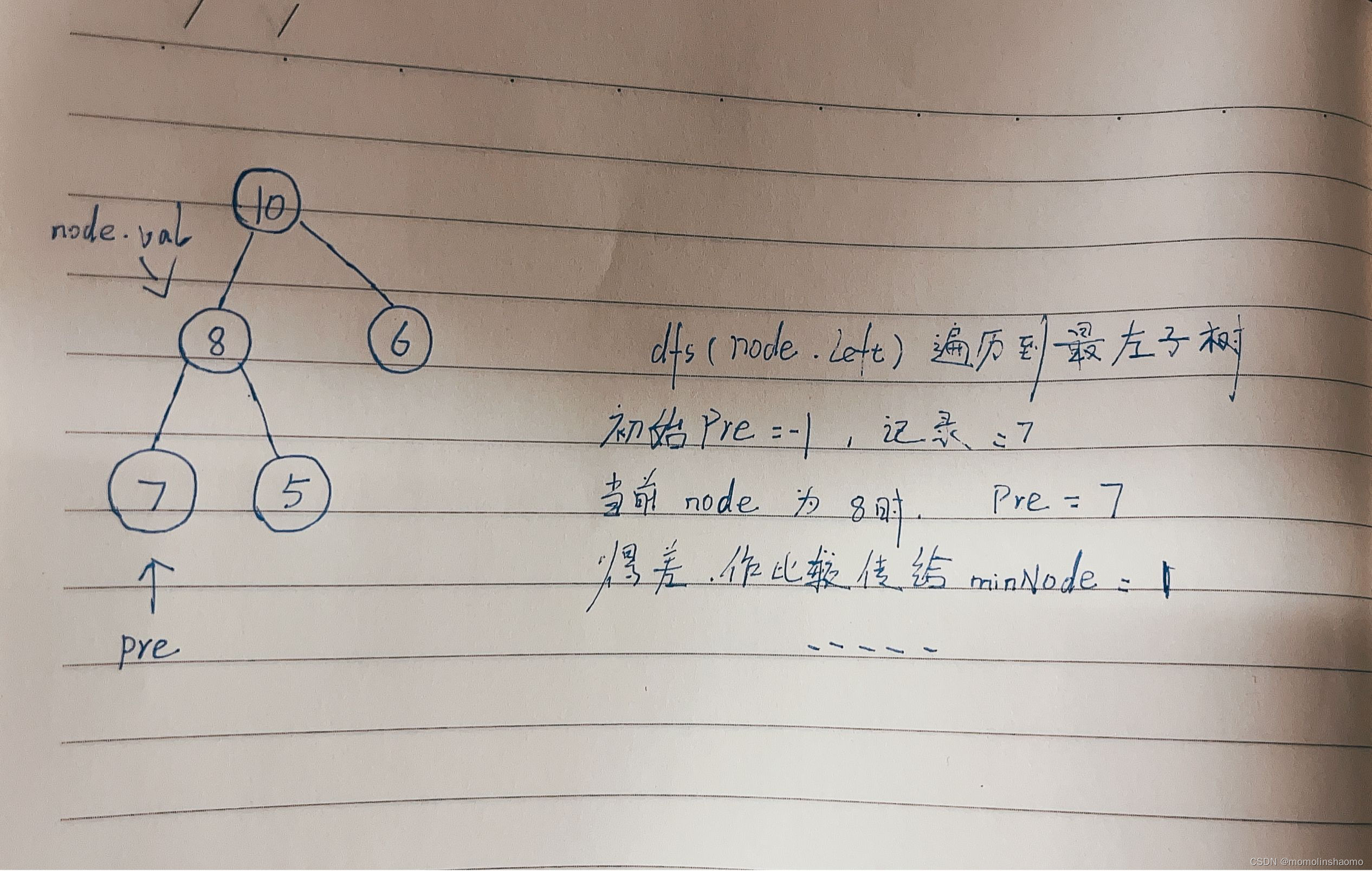
整体思路很简单：就是一个pre指针记录上一个节点的值，与当前值进行相减之后，与minNode中存储的结果作比较（minNode中肯定存放的是更小的值），这样可以更新其结果，遍历完得到最终的结果。

图解如下：

用栈模拟，迭代法：

class Solution {
    public int getMinimumDifference(TreeNode root) {
        Stack<TreeNode> stack = new Stack<>();
        TreeNode pre = null;
        int result = Integer.MAX_VALUE;

        if(root != null)
            stack.add(root);
        while(!stack.isEmpty()){
            TreeNode curr = stack.peek();
            if(curr != null){
                stack.pop();
                if(curr.right != null)
                    stack.add(curr.right);
                stack.add(curr);
                stack.add(null);
                if(curr.left != null)
                    stack.add(curr.left);
            }else{
                stack.pop();
                TreeNode temp = stack.pop();
                if(pre != null)
                    result = Math.min(result, temp.val - pre.val);
                pre = temp;
            }
        }
        return result;
    }
}

?

?

二叉搜索树中的众数：力扣题目链接

给你一个含重复值的二叉搜索树（BST）的根节点 root ，找出并返回 BST 中的所有 众数（即，出现频率最高的元素）。

如果树中有不止一个众数，可以按 任意顺序 返回。

假定 BST 满足如下定义：

• 结点左子树中所含节点的值 小于等于 当前节点的值
• 结点右子树中所含节点的值 大于等于 当前节点的值
• 左子树和右子树都是二叉搜索树

我根据上一个题的思路写了一个解法：

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    //该树是一个二叉搜索树
    List<Integer> list = new ArrayList<>();
    int pre = -1;
    int preCount = 0;
    int maxCount = 0;
    public int[] findMode(TreeNode root) {
    dfs(root);
    addMore(pre,preCount);

    int [] res = new int[list.size()];
   

    for(int i =0;i<list.size();i++){
        res[i] = list.get(i);
    }
    return res;
    }
    public void dfs(TreeNode node){
        if(node == null){
            return;
        }
        dfs(node.left);
        if(pre == -1 || pre != node.val){
           addMore(pre,preCount);
           pre = node.val;
           preCount = 1;
        }else{
            preCount++;
        }
        dfs(node.right);
    }

    public void addMore(int value,int count){
        if(count > maxCount){
            maxCount = count;
            list.clear();
            if(value != -1)
                list.add(value);
            }else if(count == maxCount && value != -1){
                list.add(value);
            }
        }
    
}

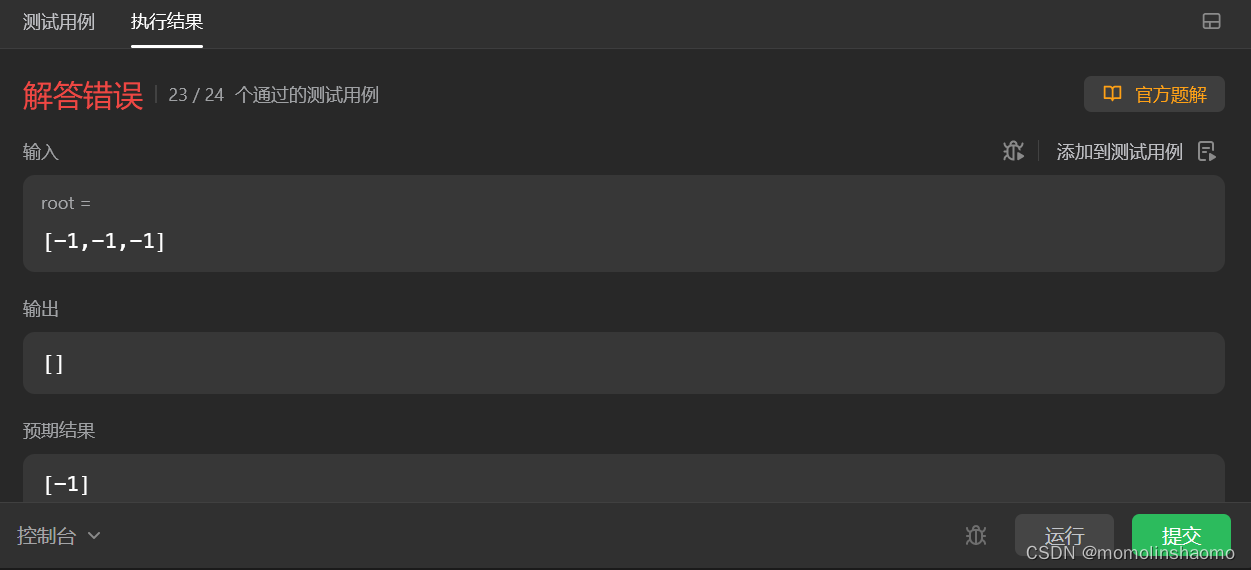
不过，这段代码不能处理以下测试：

?

?更改后的代码：

class Solution {
    ArrayList<Integer> resList;
    int maxCount;
    int count;
    TreeNode pre;

    public int[] findMode(TreeNode root) {
        resList = new ArrayList<>();
        maxCount = 0;
        count = 0;
        pre = null;
        findMode1(root);
        int[] res = new int[resList.size()];
        for (int i = 0; i < resList.size(); i++) {
            res[i] = resList.get(i);
        }
        return res;
    }

    public void findMode1(TreeNode root) {
        if (root == null) {
            return;
        }
        findMode1(root.left);

        int rootValue = root.val;
        // 计数
        if (pre == null || rootValue != pre.val) {
            count = 1;
        } else {
            count++;
        }
        // 更新结果以及maxCount
        if (count > maxCount) {
            resList.clear();
            resList.add(rootValue);
            maxCount = count;
        } else if (count == maxCount) {
            resList.add(rootValue);
        }
        pre = root;

        findMode1(root.right);
    }
}

?

?二叉树的最近公共祖先：力扣题目链接

给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。

百度百科中最近公共祖先的定义为：“对于有根树 T 的两个节点 p、q，最近公共祖先表示为一个节点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。”

用后序遍历，从后往前找！

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        if (root == null || root == p || root == q) { // 递归结束条件
            return root;
        }

        // 后序遍历
        TreeNode left = lowestCommonAncestor(root.left, p, q);
        TreeNode right = lowestCommonAncestor(root.right, p, q);

        if(left == null && right == null) { // 若未找到节点 p 或 q
            return null;
        }else if(left == null && right != null) { // 若找到一个节点
            return right;
        }else if(left != null && right == null) { // 若找到一个节点
            return left;
        }else { // 若找到两个节点
            return root;
        }
    }
}

莫思身外无穷事，

且尽生前有限杯。

Fighting！

?

?

?