343. 整数拆分(动态规划)

题目：

给定一个正整数 n ，将其拆分为 k 个 正整数 的和（ k >= 2 ），并使这些整数的乘积最大化。

返回 你可以获得的最大乘积 。

示例 1:

输入: n = 2
输出: 1
解释: 2 = 1 + 1, 1 × 1 = 1。
示例 2:

输入: n = 10
输出: 36
解释: 10 = 3 + 3 + 4, 3 × 3 × 4 = 36。

提示:

2 <= n <= 58

思路：

本题比之前面的动态规划还要难理解点，理解难度主要在动态规划递推公式的推导上和dp数组的含义理解上。本题我也是根据题解分析才理解的，写本篇博客也能更加加深自己的理解。

动规五部曲：

1. 确定dp数组（dp table）以及下标的含义

dp[i]：分拆数字i，可以得到的最大乘积为dp[i]。

dp[i]的定义将贯彻整个解题过程，下面哪一步想不懂了，就想想dp[i]究竟表示的是啥！dp[n]就是最终题解答案。

2. 确定递推公式

可以想 dp[i]最大乘积是怎么得到的呢？

其实可以从1遍历j，然后有两种渠道得到dp[i].

一个是j * (i - j) 直接相乘。

一个是j * dp[i - j]，相当于是拆分(i - j)，对这个拆分不理解的话，可以回想dp数组的定义。

j怎么就不拆分呢？

j是从1开始遍历，拆分j的情况，在遍历j的过程中其实都计算过了。那么从1遍历j，比较(i - j) * j和dp[i - j] * j 取最大的。递推公式：dp[i] = max(dp[i], max((i - j) * j, dp[i - j] * j));

也可以这么理解，j * (i - j) 是单纯的把整数拆分为两个数相乘，而j * dp[i - j]是拆分成两个以及两个以上的个数相乘。

如果定义dp[i - j] * dp[j] 也是默认将一个数强制拆成4份以及4份以上了。

所以递推公式：dp[i] = max({dp[i], (i - j) * j, dp[i - j] * j});

那么在取最大值的时候，为什么还要比较dp[i]呢？

因为在递推公式推导的过程中，每次计算dp[i]，取最大的而已。

每一趟循环中都会计算出dp[i]的数值然后用前面计算好的dp[i]（如：dp[3],dp[4]）来计算的之后的dp数组,这么说可能比较抽象，可以根据代码在纸上写下每次计算的过程和结果就好理解了。

3. dp的初始化

rendp[0] dp[1]应该初始化多少呢？

严格从dp[i]的定义来说，dp[0] dp[1] 就不应该初始化，也就是没有意义的数值。

拆分0和拆分1的最大乘积是多少？

这是无解的。

这里只初始化dp[2] = 1，从dp[i]的定义来说，拆分数字2，得到的最大乘积是1

4. 确定遍历顺序

毋庸置疑，遍历顺序肯定从前往后遍历，先来看看递归公式：dp[i] = max(dp[i], (i - j) * j, dp[i - j] * j); dp[i] 是依靠 dp[i - j]的状态，所以遍历i一定是从前向后遍历，先有dp[i - j]再有dp[i]。

        for i in range(3, n + 1):
            for j in range(1, i - 1):
                dp[i] = max(dp[i], dp[i - j] * j, j * (i - j))

注意 枚举j的时候，是从1开始的。从0开始的话，那么让拆分一个数拆个0，求最大乘积就没有意义了。

j的结束条件是 j < i - 1 ，其实 j < i 也是可以的，不过可以节省一步，例如让j = i - 1，的话，其实在 j = 1的时候，这一步就已经拆出来了，重复计算，所以 j < i - 1

至于 i是从3开始，这样dp[i - j]就是dp[2]正好可以通过我们初始化的数值求出来。

更优化一步，可以这样：

        for i in range(3, n + 1):
            for j in range(1, i - 1):
                dp[i] = max(dp[i], dp[i - j] * j, j * (i - j))

因为拆分一个数n 使之乘积最大，那么一定是拆分成m个近似相同的子数相乘才是最大的。

例如 6 拆成 3 * 3， 10 拆成 3 * 3 * 4。 100的话 也是拆成m个近似数组的子数 相乘才是最大的。

只不过我们不知道m究竟是多少而已，但可以明确的是m一定大于等于2，既然m大于等于2，也就是 最差也应该是拆成两个相同的 可能是最大值。

那么 j 遍历，只需要遍历到 n/2 就可以，后面就没有必要遍历了，一定不是最大值。

5. 举例推导dp数组

举例当n为10 的时候，dp数组里的数值，如下：

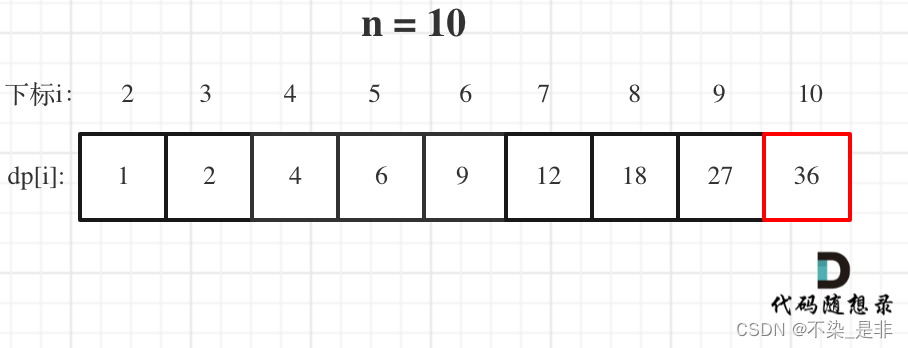
代码及详细注释：

class Solution:
    def integerBreak(self, n: int) -> int:
        # 创建一个长度为 n+1 的数组，用于存储最大乘积结果
        dp = [0] * (n + 1)
        dp[2] = 1  # 当 n=2 时，最大乘积为 1

        # 遍历从 3 到 n 的每个数字
        for i in range(3, n + 1):
            # 遍历从 1 到 i-1 的每个数字
            for j in range(1, i - 1):
                # 计算当前数字 i 的最大乘积
                dp[i] = max(dp[i], dp[i - j] * j, j * (i - j))
        # 返回数字 n 的最大乘积
        return dp[n]

• 时间复杂度：O(n^2)
• 空间复杂度：O(n)