day29 递增子序列 全排列 全排列Ⅱ

题目1：491 递增子序列

题目链接：491 递增子序列

题意

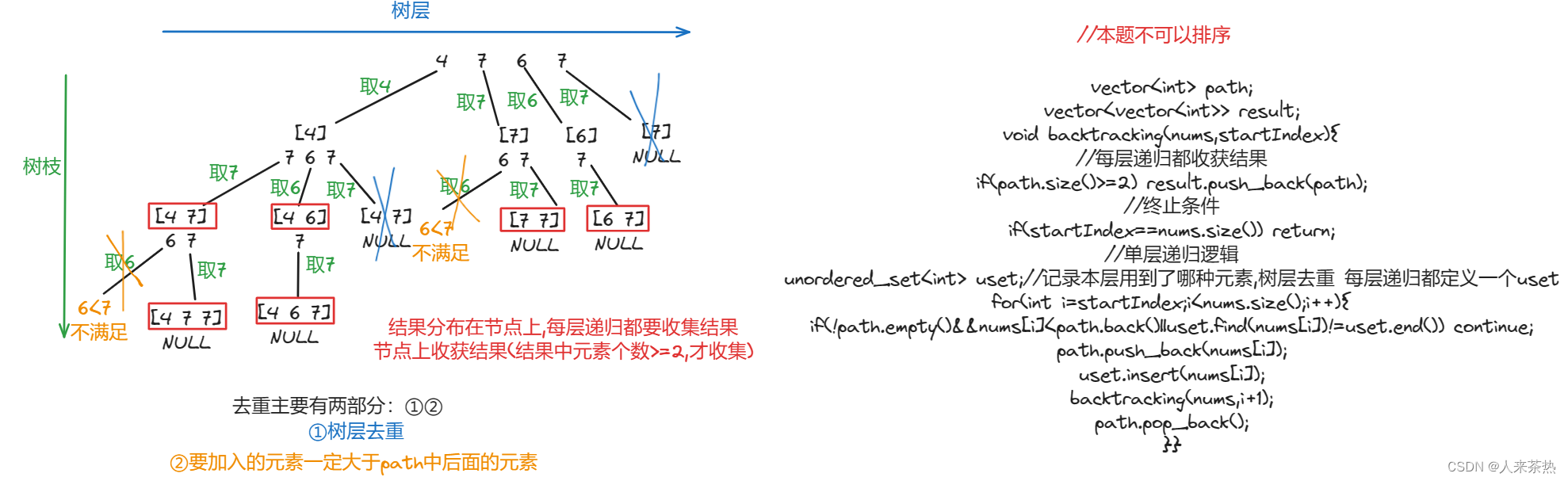
整数数组nums中可能存在重复元素，求不同的递增子序列（至少有2个元素），若两个整数相等，也是递增子序列

本题不可以排序，需要保证原数组的顺序不变 去重逻辑和前面的题目不同

去重主要包含两个部分：1）树层去重? ?2）要加入的元素大于path中最后面的元素

每层递归都要收获结果（path.size()>=2）

回溯

回溯三部曲：

1）参数和返回值

2）终止条件

3）单层递归逻辑

代码

class Solution {
public:
    vector<int> path;
    vector<vector<int>> result;
    void backtracking(vector<int>& nums,int startIndex){
        if(path.size()>=2) result.push_back(path);
        //终止条件
        if(startIndex==nums.size()) return;
        //单层搜索逻辑
        unordered_set<int> uset;
        for(int i=startIndex;i<nums.size();i++){
            if(!path.empty() && nums[i]<path.back() || uset.find(nums[i])!=uset.end()) continue;
            path.push_back(nums[i]);
            uset.insert(nums[i]);
            backtracking(nums,i+1);
            path.pop_back();
        }
    }
    vector<vector<int>> findSubsequences(vector<int>& nums) {
        backtracking(nums,0);
        return result;
    }
};

• 时间复杂度: O(n * 2^n)
• 空间复杂度: O(n)

优化（unordered_set改用数组）

unordered_set 频繁的insert，需要做哈希映射（也就是把key通过hash function映射为唯一的哈希值）相对费时间，而且每次重新定义set，insert的时候其底层的符号表也要做相应的扩充，也费时

代码

class Solution {
public:
    vector<int> path;
    vector<vector<int>> result;
    void backtracking(vector<int>& nums,int startIndex){
        if(path.size()>=2) result.push_back(path);//这里不可以return 因为后面还要递归继续收集结果
        //终止条件
        if(startIndex==nums.size()) return;
        //单层搜索逻辑
        int used[201] = {0};//数组的数值大小是-100~100 共200个key  0~200的下标对应nums中-100~100的值
        for(int i=startIndex;i<nums.size();i++){
            if(!path.empty() && nums[i]<path.back() || used[nums[i]+100]==1) continue;
            path.push_back(nums[i]);
            used[nums[i]+100] = 1;//转化为0~200内的值
            backtracking(nums,i+1);
            path.pop_back();
        }
    }
    vector<vector<int>> findSubsequences(vector<int>& nums) {
        backtracking(nums,0);
        return result;
    }
};

题目2：46 全排列

题目链接：46 全排列

题意

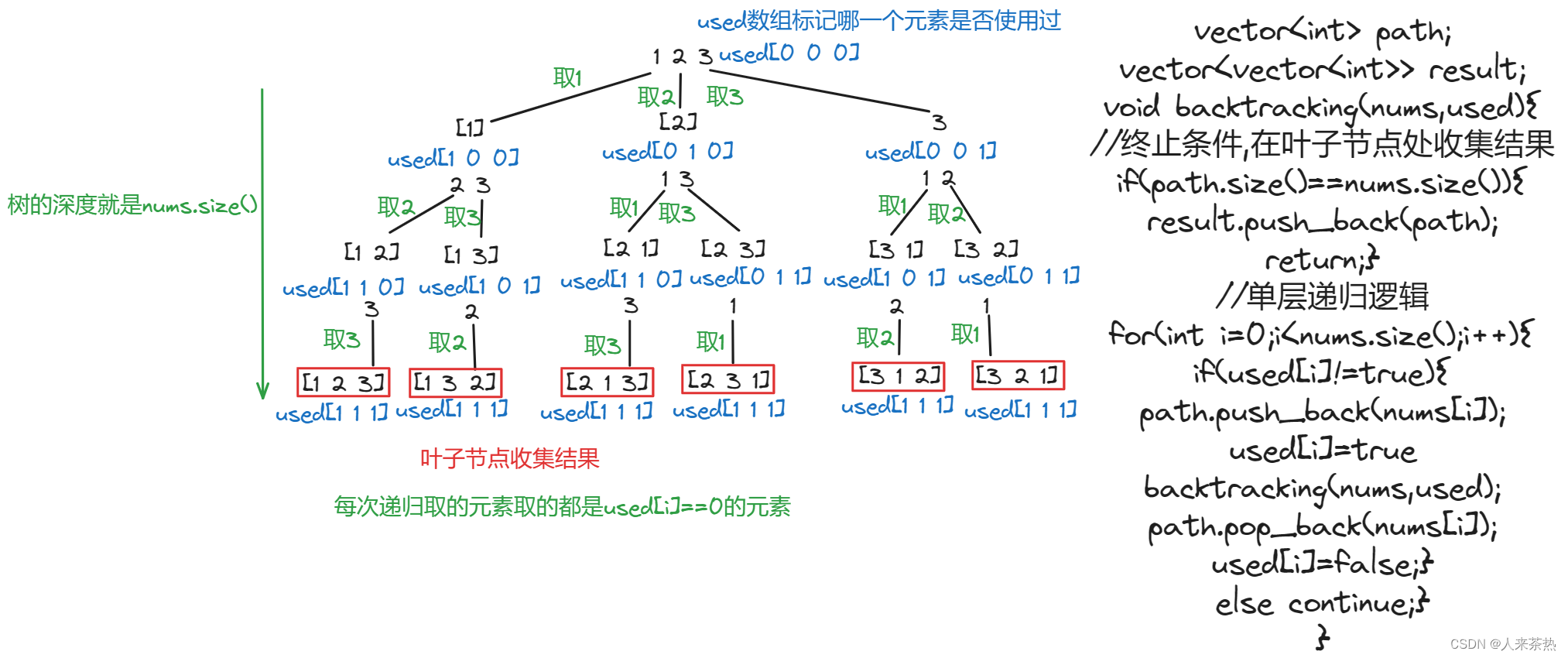
返回无重复元素的整数数组nums的所有全排列

回溯

回溯三部曲：

1）参数和返回值

2）终止条件

3）单层递归逻辑

注意排列和组合是不一样的，[1 2] [2 1]是两个全排列? ?是同一个组合，因此处理排列就不使用startIndex避免重复取元素更新下标了，每次从数组开头查询元素是否用过，若用过，则跳过继续判断下一个元素，若没用过，则放入到path中进入下一层递归

代码

class Solution {
public:
    vector<int> path;
    vector<vector<int>> result;
    void backtracking(vector<int>& nums,vector<bool> used){
        //终止条件,叶子节点收集结果
        if(path.size()==nums.size()){
            result.push_back(path);
            return;
        }
        //单层搜索逻辑
        for(int i=0;i<nums.size();i++){
            if(used[i]!=true){
                path.push_back(nums[i]);
                used[i] = true;
                backtracking(nums,used);
                path.pop_back();
                used[i] = false;
            }
        }
    }
    vector<vector<int>> permute(vector<int>& nums) {
        vector<bool> used(nums.size(),false);
        backtracking(nums,used);
        return result;
    }
};

• 时间复杂度: O(n!)
• 空间复杂度: O(n)

题目3：47 全排列Ⅱ

题目链接：47 全排列Ⅱ

题意

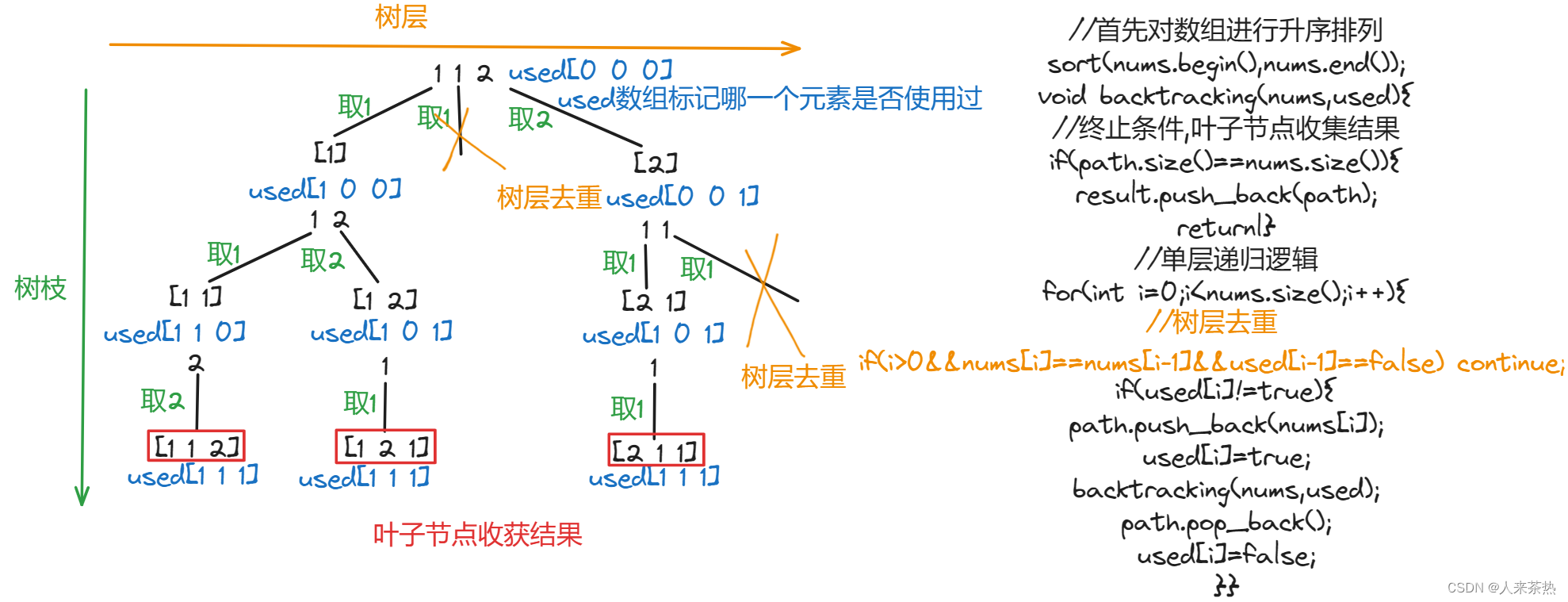
整数数组nums中包含重复数字，返回所有全排列（不重复）

主要是去重逻辑，去重前记得排序

回溯

回溯三部曲：

1）参数和返回值

2）终止条件

3）单层搜索逻辑

代码

class Solution {
public:
    vector<int> path;
    vector<vector<int>> result;
    void backtracking(vector<int>& nums,vector<bool> used){
        //终止条件
        if(path.size()==nums.size()){
            result.push_back(path);
            return;
        }
        //单层搜索逻辑
        for(int i=0;i<nums.size();i++){
            if(i>0 && nums[i]==nums[i-1] && used[i-1]==false) continue;//树层去重
            if(used[i]!=true){
                path.push_back(nums[i]);
                used[i] = true;
                backtracking(nums,used);//递归
                path.pop_back();
                used[i] = false;
            }
        }
    }
    vector<vector<int>> permuteUnique(vector<int>& nums) {
        sort(nums.begin(),nums.end());
        vector<bool> used(nums.size(),false);
        backtracking(nums,used);
        return result;
    }
};

• 时间复杂度: O(n! * n)
• 空间复杂度: O(n)