强化学习（二）多臂老虎机 “Multi-armed Bandits”——2

1、增量算法估计动作价值

由之前的内容可知，某一个动作被选择 $n?1$ 次后，该动作的价值估计值为
$$Q_n?\frac{R_1+R_2+?+R_{n?1}}{n?1}$$

很明显，随着时间的推移，内存和计算的需求逐渐增长，为此设计增量算法，已知 $Q_n$ 和第 $n$ 次的奖励 $R_n$，则这 $n$ 次奖励的新平均值计算如下：
$$\begin{array}{rl}{Q}_{n+1}& =\frac{1}{n}\sum _{i=1}^n{R}_i\\ & =\frac{1}{n}(R_n+\sum _{i=1}^{n?1}{R}_i)\\ & =\frac{1}{n}(R_n+(n?1)\frac{1}{n?1}\sum _{i=1}^{n?1}{R}_i)\\ & =\frac{1}{n}(R_n+(n?1)Q_n)\\ & =\frac{1}{n}(R_n+n{Q}_n?Q_n)\\ & =Q_n+\frac{1}{n}[R_n?Q_n]\end{array}$$

这种方法只需要 $Q_n$ 和 $n$ 的内存，且每次只需要很小的计算量。这是一种后面会经常出现的形式，其一般表示为：
$$NewEstimate\leftarrow OldEstimate+StepSize[Target?OldEstimate]$$

其中 $[Target?OldEstimate]$ 是估计的误差，它通过向“目标”靠近来降低。在增量算法中使用的步长参数（$StepSize$）随时间而变化，该方法用的是 $\frac{1}{n}$，后续我们一般用 $\alpha$ 或 ${\alpha }_t(a)$ 来表示步长参数。

下面展示使用增量算法计算样本平均值以及 $??$ 贪心算法的伪代码

2、奖励随时间变化问题

目前未知，我们讨论的方法都是基于奖励不随时间变化的问题，而对于奖励随时间变化的情况下，我们一般侧重于近期奖励，即给予近期奖励比以往奖励更多的权重。最常用的方法之一就是用定步长参数，
$$Q_{n+1}?Q_n+\alpha [R_n?Q_n]$$

其中步长参数 $\alpha \in (0,1]$ 为常数，这就导致 $Q_{n+1}$ 是过去奖励与初始估计 $Q_1$的加权平均值
$$\begin{array}{rl}{Q}_{n+1}& =Q_n+\alpha [R_n?Q_n]\\ & =\alpha R_n+(1?\alpha )Q_n\\ & =\alpha R_n+(1?\alpha )[\alpha R_{n?1}+(1?\alpha )Q_{n?1}]\\ & =\alpha R_n+(1?\alpha )\alpha R_{n?1}+(1?\alpha {)}^2{Q}_{n?1}\\ & =(1?\alpha {)}^n{Q}_1+\sum _{i=1}^n\alpha (1?\alpha {)}^{n?i}{R}_i\end{array}$$

为什么称其为加权平均，因为权重之和 $(1?\alpha {)}^n+{\sum }_{i=1}^n\alpha (1?\alpha {)}^{n?i}=1$。另外可以看出，$R_i$ 的权重随着奖励数量的增加而减小，因此我们也称为指数近期加权平均（exponential recency-weighted average）。

接下来我们讨论一下变步长参数。设 ${\alpha }_n(a)$ 为第 $n$ 次选择动作 $a$ 时，用于处理所获奖励的步长参数。如前所述，${\alpha }_n(a)=\frac{1}{n}$，该方法由大数定律可以保证动作价值的估计值收敛于其真实值。当然并不是所有的变步长都保证收敛，可以保证以概率 1 收敛的必要条件是：
$$\sum _{n=1}^{\infty }{\alpha }_n(a)=\infty and\sum _{n=1}^{\infty }{\alpha }_n^2(a)<\infty$$

这两个收敛条件可以理解为：第一个条件要保证步长足够大，从而克服任何的初始条件或随机波动；第二个条件保证最终步长变小到足以保证收敛。由此可以看出，对于 ${\alpha }_n(a)=\frac{1}{n}$ 满足两个收敛条件，而对于 ${\alpha }_n(a)=\alpha$ 不满足第二个收敛条件，这表明估计值一直不会完全收敛，而是继续变化以相应最近收到的奖励，这对于奖励随时间变化的情况是有利的，此外满足上述两个收敛条件的步长参数往往收敛速度很慢，因此实际中很少使用。

3、初始值

到目前为止，所有讨论的方法都在一定程度上依赖初始的动作价值估计 $Q_1(a)$，也就是说这些方法都会因为 $Q_1(a)$ 的取值而产生偏差。对于样本平均方法，一旦所有动作至少被选择一次，那么偏差就会消失，但是对于定步长参数的方法，偏差会随着时间的推移而减少但不会消失。这其实有好有坏，不利的一面是，初始值设定变成了一组必须用户进行挑选的参数；有利的一面是，这也提供了一种简单的方法，通过合理设置初始值从而加快收敛速度。

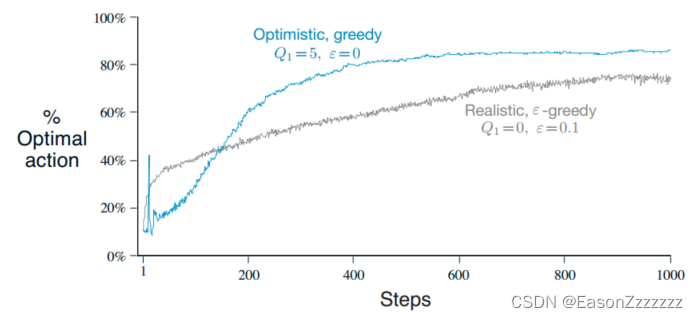
初始动作价值的设定也可以作为鼓励探索的简单方法，例如之前的多臂老虎机问题，其真实动作价值 $q_{?}$ 服从期望为 0，方差为 1 的正态分布，若我们将初始动作价值估计设为 5，那么无论选择哪种动作，奖励都小于初始的动作价值估计，那么无论是完全的贪心方法还是 $??$ 贪心方法，系统总是会进行相当数量的探索。

代码部分

import numpy as np
import matplotlib.pyplot as plt

# 初始值设定
step = 2000
alpha = 0.1

q_true = np.random.normal(0, 1, 10)  # 真实的动作价值
optimal_true = np.argmax(q_true)  # 最优动作
q_estimate1 = np.zeros(10)  # 估计的动作价值
q_estimate2 = np.full(10, 5.1)  # 估计的动作价值

epsilon1 = 0.9  # 贪心概率
epsilon2 = 0.9  # 贪心概率

optimal_count1 = 0
optimal_count2 = 0
optimal_probability1 = np.zeros(step)
optimal_probability2 = np.zeros(step)
action_space = [0, 1, 2, 3, 4, 5, 6, 7, 8, 9]

for i in range(step):
    if (np.random.uniform() > epsilon1) or (q_estimate1.all() == 0):
        machine_name = np.random.choice(action_space)
        if machine_name == optimal_true:
            optimal_count1 += 1
        optimal_probability1[i] = 100 * optimal_count1 / (i+1)
        reward = np.random.normal(q_true[machine_name], 1, 1)
        q_estimate1[machine_name] = q_estimate1[machine_name] + alpha * (reward - q_estimate1[machine_name])
    else:
        machine_name = np.argmax(q_estimate1)
        if machine_name == optimal_true:
            optimal_count1 += 1
        optimal_probability1[i] = 100 * optimal_count1 / (i + 1)
        reward = np.random.normal(q_true[machine_name], 1, 1)
        q_estimate1[machine_name] = q_estimate1[machine_name] + alpha * (reward - q_estimate1[machine_name])

for i in range(step):
    if (np.random.uniform() > epsilon1) or (q_estimate2.all() == 5):
        machine_name = np.random.choice(action_space)
        if machine_name == optimal_true:
            optimal_count2 += 1
        optimal_probability2[i] = 100 * optimal_count2 / (i+1)
        reward = np.random.normal(q_true[machine_name], 1, 1)
        q_estimate2[machine_name] = q_estimate2[machine_name] + alpha * (reward - q_estimate2[machine_name])
    else:
        machine_name = np.argmax(q_estimate2)
        if machine_name == optimal_true:
            optimal_count2 += 1
        optimal_probability2[i] = 100 * optimal_count2 / (i + 1)
        reward = np.random.normal(q_true[machine_name], 1, 1)
        q_estimate2[machine_name] = q_estimate2[machine_name] + alpha * (reward - q_estimate2[machine_name])

plt.plot(optimal_probability1, label="Q1 = 0, e = 0.1")
plt.plot(optimal_probability2, label="Q1 = 5.1, e = 0.1")

plt.xlabel('Steps')
plt.ylabel('Optimal action')
plt.legend()
plt.show()