强化学习12——策略梯度算法学习

Q-learning、DQN算法是基于价值的算法，通过学习值函数、根据值函数导出策略；而基于策略的算法，是直接显示地学习目标策略，策略梯度算法就是基于策略的算法。

策略梯度介绍

将策略描述为带有参数 $\theta$ 的连续函数，可以将策略学习的目标函数定义为：
$$J(\theta )={\mathbb{E}}_{s_0}[V^{{\pi }_{\theta }}(s_0)]$$
我们将目标函数对参数 $\theta$ 求导，得到导数，就可以用梯度上升方法来最大化目标函数，从而得到最优策略。

我们使用 ${\nu }^{\pi }$ 表示策略 $\pi$ 下的状态访问分布，得到如下式子：

$$\begin{array}{rl}{?}_{\theta }J(\theta )& \propto \sum _{s\in S}{\nu }^{{\pi }_{\theta }}(s)\sum _{a\in A}{Q}^{{\pi }_{\theta }}(s,a){?}_{\theta }{\pi }_{\theta }(a|s)\\ & =\sum _{s\in S}{\nu }^{{\pi }_{\theta }}(s)\sum _{a\in A}{\pi }_{\theta }(a|s)Q^{{\pi }_{\theta }}(s,a)\frac{{?}_{\theta }{\pi }_{\theta }(a|s)}{{\pi }_{\theta }(a|s)}\\ & ={\mathbb{E}}_{{\pi }_{\theta }}[Q^{{\pi }_{\theta }}(s,a){?}_{\theta }\log {\pi }_{\theta }(a|s)]\end{array}$$
上式中期望的下标是 ${\pi }_{\theta }$ ，因此对应的是使用当前策略 ${\pi }_{\theta }$ 进行采样并计算梯度，通过梯度的修改，让策略更多地采样到较高Q值的动作。

如上图所示，如果动作a1可以带来的价值更高，那么a1的概率会增大，对应的是a1的柱子变高。

在REINFORCE算法中，采用蒙特卡洛方法来估计 $Q^{{\pi }_{\theta }}(s,a)$ ，对于一个有限步数的环境，该算法如下式所示：

$${?}_{\theta }J(\theta )={\mathbb{E}}_{{\pi }_{\theta }}\left[\sum _{t=0}^T\left(\sum _{t^{\prime }=t}^T{\gamma }^{t^{\prime }?t}{r}_{t^{\prime }}\right){?}_{\theta }\log {\pi }_{\theta }(a_t|s_t)\right]$$

REINFORCE算法介绍

具体流程如下所示：

• 初始化策略参数 $\theta$
• for 序列 $e=1\to E$ do:
  • 用当前策略 ${\pi }_{\theta }$ 采样轨迹 { s 1 , a 1 , r 1 , s 2 , a 2 , r 2 , … s T , a T , r T } \{s_{1},a_{1},r_{1},s_{2},a_{2},r_{2},\ldots s_{T},a_{T},r_{T}\} {s1?,a1?,r1?,s2?,a2?,r2?,…sT?,aT?,rT?}
  • 计算当前轨迹每个时刻的回报${\sum }_{t^{\prime }=t}^T{\gamma }^{t^{\prime }?t}{r}_{t^{\prime }}$ ，记为${\psi }_t$
  • 对 $\theta$ 进行更新，$\theta =\theta +\alpha {\sum }_t^T{\psi }_t{?}_{\theta }\log {\pi }_{\theta }(a_t|s_t)$

• end for

代码实践

import gymnasium as gym
import torch
import torch.nn.functional as F
import numpy as np
import matplotlib.pyplot as plt
from tqdm import tqdm
import rl_utils

# 定义一个策略网络，输入是某个状态，输出是该状态下的动作概率分布
# 通过softmax函数，输出概率分布
class PolicyNet(torch.nn.Module):
    def __init__(self, state_dim, hidden_dim, action_dim):
        super(PolicyNet, self).__init__()
        self.fc1 = torch.nn.Linear(state_dim, hidden_dim)
        self.fc2 = torch.nn.Linear(hidden_dim, action_dim)

    def forward(self, x):
        x = F.relu(self.fc1(x))
        return F.softmax(self.fc2(x), dim=1)

定义REINFORCE算法，以策略回报的1负数来表示损失函数，即$?{\sum }_t{\psi }_t{?}_{\theta }\log {\pi }_{\theta }(a_t|s_t)$

class REINFORCE:
    def __init__(self, state_dim, hidden_dim, action_dim,learning_rate,gamma,device):
        self.state_dim = state_dim
        self.action_dim = action_dim
        # 初始化策略网络
        self.policy_net = PolicyNet(state_dim, hidden_dim, action_dim).to(device)
        self.optimizer = torch.optim.Adam(params=self.policy_net.parameters(), lr=learning_rate)
        self.gamma = gamma
        self.device = device
        
    def take_aciton(self, state):
        # 根据动作概率分布随机采样
        state = torch.tensor([state],dtype=torch.float).to(self.device)
        action_prob = self.policy_net(state)
        # 根据每个动作的概率进行采样
        action_dist = torch.distributions.Categorical(action_prob)
        action = action_dist.sample()
        # 返回是哪个动作，类型为标量
        return action.item()
    
    def update(self, transition_dict):
        reward_list = transition_dict['rewards']
        state_list = transition_dict['states']
        action_list = transition_dict['actions']
        G=0
        self.optimizer.zero_grad()
        for i in reversed(range(len(reward_list))): #从最后一步算起
            reward=reward_list[i]
            G=reward+self.gamma*G
            state=torch.tensor([state_list[i]],dtype=torch.float).to(self.device)
            action=torch.tensor([action_list[i]]).view(-1,1).to(self.device)
            log_prob = torch.log(self.policy_net(state).gather(1, action))
            loss=-log_prob*G #每一步的损失哈桑农户
            loss.backward() # 反向传播计算梯度
        self.optimizer.step() # 梯度下降

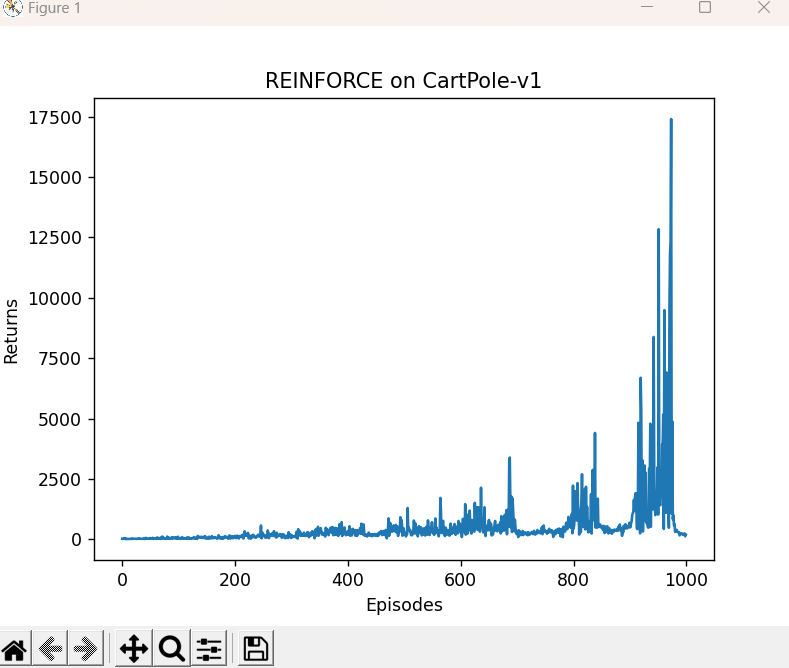
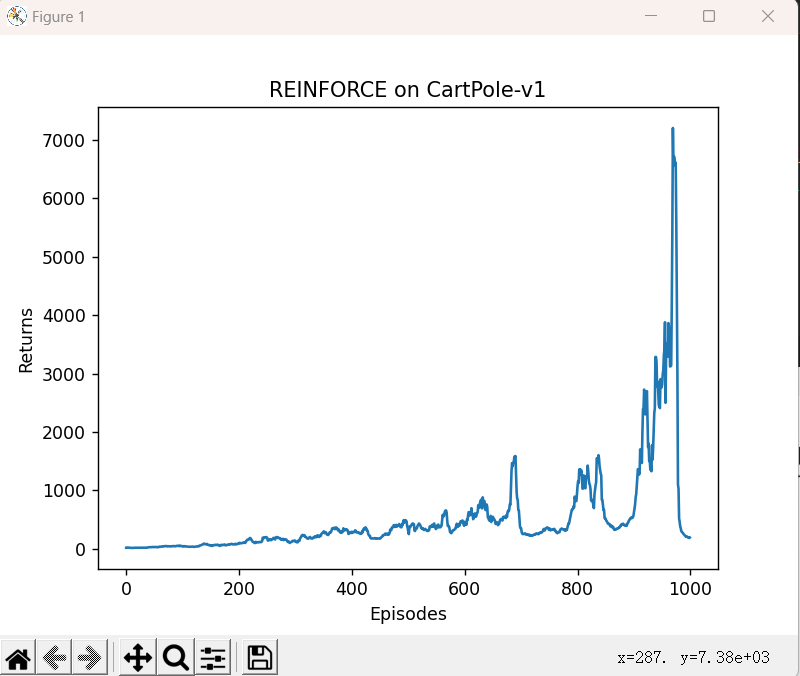
由于采用蒙特卡洛方法，REINFORCE算法的梯度估计的方差很大，会产生不稳定性，造成回报曲线的抖动。在我们对结果进行平滑处理后，可以得到较为光滑的曲线。

learning_rate = 1e-3
num_episodes = 1000
hidden_dim = 128
gamma = 0.98
device = torch.device("cuda") if torch.cuda.is_available() else torch.device(
    "cpu")

env_name = "CartPole-v1"
env = gym.make(env_name)
torch.manual_seed(0)
state_dim = env.observation_space.shape[0]
action_dim = env.action_space.n
agent = REINFORCE(state_dim, hidden_dim, action_dim, learning_rate, gamma,
                  device)
return_list = []
for i in range(10):
    with tqdm(total=int(num_episodes / 10), desc='Iteration %d' % i) as pbar:
        for i_episode in range(int(num_episodes / 10)):
            episode_return = 0
            transition_dict = {
                'states': [],
                'actions': [],
                'next_states': [],
                'rewards': [],
                'dones': []
            }
            state = env.reset()[0]
            done = False
            while not done:
                action = agent.take_action(state)
                next_state, reward, done, info, _= env.step(action)
                transition_dict['states'].append(state)
                transition_dict['actions'].append(action)
                transition_dict['next_states'].append(next_state)
                transition_dict['rewards'].append(reward)
                transition_dict['dones'].append(done)
                state = next_state
                episode_return += reward
            return_list.append(episode_return)
            agent.update(transition_dict)
            if (i_episode + 1) % 10 == 0:
                pbar.set_postfix({
                    'episode':
                    '%d' % (num_episodes / 10 * i + i_episode + 1),
                    'return':
                    '%.3f' % np.mean(return_list[-10:])
                })
            pbar.update(1)
            
episodes_list = list(range(len(return_list)))
plt.plot(episodes_list, return_list)
plt.xlabel('Episodes')
plt.ylabel('Returns')
plt.title('REINFORCE on {}'.format(env_name))
plt.show()

mv_return = rl_utils.moving_average(return_list, 9)
plt.plot(episodes_list, mv_return)
plt.xlabel('Episodes')
plt.ylabel('Returns')
plt.title('REINFORCE on {}'.format(env_name))
plt.show()