入局CV，Mamba再显神威！华科王兴刚团队首次将Mamba引入ViT，更高精度、更快速度、更低显存！

本文首发: AIWalker

在Transformer如日中天时，一个称之为“Mamba”的架构横冲出世，在语言建模上与Transformers不相上下，具有线性复杂度，同时具有5倍的推理吞吐量！一时之间，被给予厚望“下一代架构”~

就在今日，华中科技大学王兴刚团队首次将“Mamda”里面引入到CV领域而得到Vim公开了，比DeiT精度更高、速度更快，还节省GPU显存，神了，估计后续会出现各种变种，DeiM、PvM，哈哈~

https://arxiv.org/abs/2401.09417
https://github.com/hustvl/Vim

最近，具有高效硬件感知设计的状态空间模型(State Space Models, SSM)曼巴，已显示出在长序列建模方面的巨大潜力。虽然基于SSM构建高效和通用的视觉骨干是一个有吸引力的方向。但是，由于视觉数据的位置敏感性、视觉理解所需要的全局上下文依赖性，表示视觉数据对于SSM而言是一项具有挑战性的任务。因此，我们提出了一个新的基于双向曼巴块（Vim）的通用视觉骨干，该模型通过位置嵌入标记图像序列并通过双向状态空间模型压缩视觉表示。
在ImageNet分类、COCO检测和ADE20K语义分割任务上，Vim实现了与成熟ViT(如DeiT)相比更高的性能，同时显著提高了计算和内存效率。例如，与DeiT相比，在对分辨率为1248×1248的图像进行批量推理时，Vim快了2.8倍同时可节省86.8%的GPU内存。这些结果表明，Vim具有克服ViT处理高分辨率图像时的计算和内存限制的潜力，并有可能成为下一代视觉基础模型。

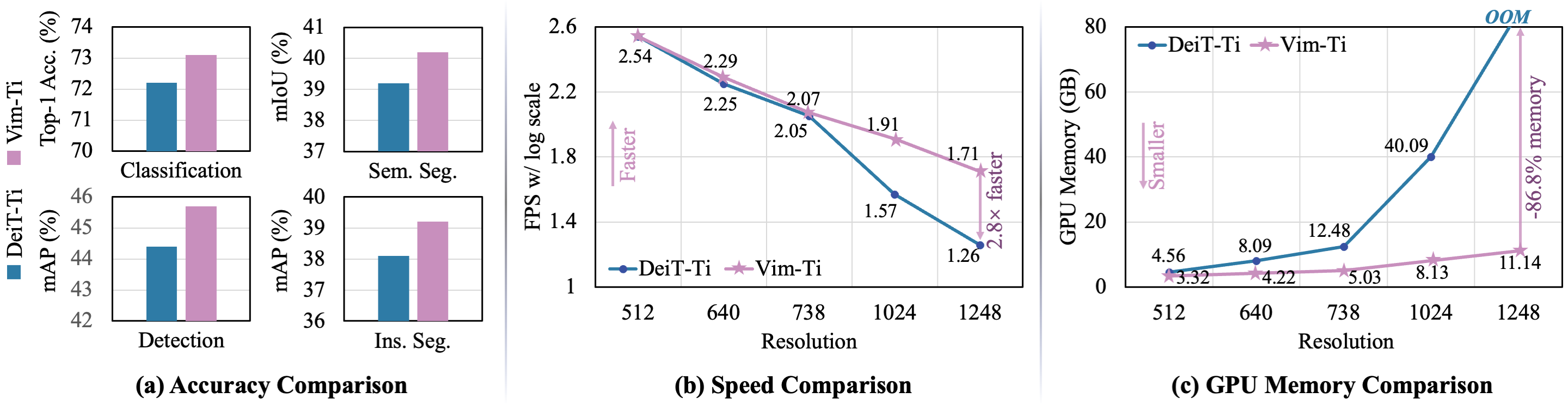
本文方案

本文所提Vim(Vision Mamba)旨在将陷阱的SSM模型(如Mamba)引入到CV领域，故先对SSM进行简要介绍，然后再介绍如何结合CV任务特性进行Vim模块设计，最后呈现所提Vim架构细节。

Preliminaries

SSM类模型(如S4)与Mamba灵感源自于连续系统，它通过隐状态$h(t)\in {\mathbb{R}}^N$将1D函数或序列$x(t)\in \mathbb{R}$y映射到$y(t)\in \mathbb{R}$，即$x(t)\in \mathbb{R}?y(t)\in \mathbb{R}$。该系统采用$\mathbf{A}\in {\mathbb{R}}^{N\times N}$表示进化参数，${\mathbf{B}}^{1\times N},\mathbf{C}\in {\mathbb{R}}^{1\times N}$则表示投影参数。

$$\begin{array}{rl}{h}^{{}^{\prime }}(t)& =\mathbf{A}h(t)+\mathbf{B}x(t)\\ y(t)& =\mathbf{C}{h}^{{}^{\prime }}(t)\end{array}\text{\hspace{1em}?}$$

S4与Mamba均为连续系统的离散版本，它引入时间尺度参数$\Delta$将连续参数$\mathbf{A},\mathbf{B}$变换为离散参数$\overline{\mathbf{A}},\overline{\mathbf{B}}$。通用ZOH方案描述如下：

$$\begin{array}{rl}\overline{\mathbf{A}}& =exp(\Delta \mathbf{A})\\ \overline{\mathbf{B}}& =(\Delta \mathbf{A}{)}^{?1}(exp(\Delta \mathbf{A})?I)?\Delta \mathbf{B}\end{array}\text{\hspace{1em}?}$$

带入上述离散参数，前述连续系统搞的离散版本重写如下：

$$
\begin{align}
h_t &= \overline{\mathbf{A}} h_{t-1} + \overline{\mathbf{B}} x_t \
y_t &= \mathbf{C}h_t

\end{align}
$$

最后，通过全局卷积计算模型输出：

$$\begin{array}{rl}\overline{\mathbf{K}}& =(\mathbf{C}\overline{\mathbf{B}},\mathbf{C}\overline{\mathbf{AB}},?,\mathbf{C}{\overline{\mathbf{A}}}^{M?1}\overline{\mathbf{B}})\\ \mathbf{y}& =\mathbf{x}?\overline{\mathbf{K}}\end{array}\text{\hspace{1em}?}$$

注：M为输入序列x的长度，$\overline{\mathbf{K}}\in {\mathbf{R}}^M$表示结构化卷积核。

Vision Mamba

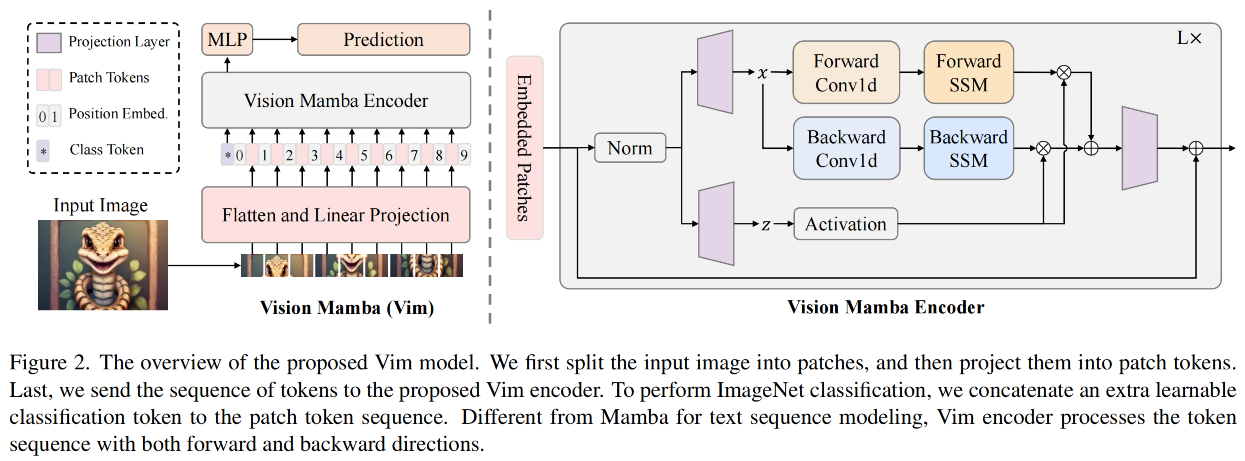
上图给出了所提Vim示意图，标准Mamba是针对1D序列而设计。为更好的处理视觉任务，我们首先将2D图$t\in {\mathbb{R}}^{H\times W\times C}$变换为2D块${\mathbf{x}}_p\in {\mathbb{R}}^{J\times (p^2?C)}$；然后，我们对其进行线性投影到D维并添加位置嵌入${\mathbf{E}}_{pos}\in {\mathbb{R}}^{(J+1)\times D}$：

$${\mathbf{T}}_0=[{\mathbf{t}}_{cls};{\mathbf{t}}_p^1\mathbf{W};{\mathbf{t}}_p^2\mathbf{W};?;{\mathbf{t}}_p^J\mathbf{W}]+{\mathbf{E}}_{pos}$$

受启发于ViT与BERT，我们同样采用类别Token(即${\mathbf{t}}_{cls}$)表示完整块序列。我们将Token序列（${\mathbf{T}}_{l?1}$）送入到第$l$个Vim编码器并得到输出${\mathbf{T}}_l$。最后，我们对${\mathbf{T}}_L^0$进行规范化并送入到MLP头得到最终预测$\hat{p}$。

$$\begin{array}{rl}{\mathbf{T}}_l& =\mathbf{Vim}({\mathbf{T}}_{l?1})+{\mathbf{T}}_{l?1}\\ \mathbf{f}& =\mathbf{Norm}({\mathbf{T}}_L^0)\\ \hat{p}& =\mathbf{MLP}(\mathbf{f})\end{array}\text{\hspace{1em}?}$$

注：Vim表示所提模块，L表示层数，Norm表示规范化层。

Vim Block

原始Mamba模块针对1D序列而设计，不适合需要空域位置感知的视觉任务。针对此，我们引入了Vim模块，它为视觉任务引入了双向序列建模机制。Vim处理流程还是看代码吧~

架构细节

总体而言，所提Vim架构有四个超参：模块数L，隐状态维度D、扩展状态维度E以及SSM维度N。

延续ViT与DeiTy，我们首先采用$16\times 16$核投影层得到1D非重叠块嵌入序列，然后直接堆叠L个Vim模块。默认信息，设置L=24，N=16。为对齐DeiT系列，Tiny版本的D=192，E=384；Small版本的D=384，E=768.

本文实验

ImageNet分类

上表给出了所提Vim与其他方案的性能对比，可以看到：

• 相比ResNet，Vim具有优异性能。如Vim-Small取得了80.3%，高出4.1%；
• 相比ViT，Vim在参数量与分类精度方面以显著优势胜出；
• 相比DeiT，Vim以相当参数量取得更高精度，如Vim-Tiny比DeiT-Tiny高出0.9%；
• 相比SSM类方案，Vim取得了相当精度，但参数量少3倍。

ADE20K语义分割

上表为ADE20K语义分割任务上不同方案性能对比，可以看到：

• Vim在不同尺度均优于DeiT，Vim-Ti比DeiT-Ti高出1.0mIoU、Vim-S比DeiT-S高出0.9mIoU。
• 相比ResNet101，Vim-S以更少的参数量取得了相当的分割精度。
• 下图从FPS与GPU占用维度进一步验证了所提方案的高效性。

COCO检测分割

上表给出了COCO实例分割任务上的性能对比，可以看到：

• Vim-Ti比DeiT-Ti高出1.3boxAp、1.1maskAP。
• 对于中等大小目标与Vim-Ti指标高出1.6boxAP、1.3maskAP；对与大尺度目标，Vim-Ti指标高出1.4boxAP、1.8maskAP。这进一步验证了Vim具有比DeiT更优的长程上下文建模能力，可参考下图。