005、Softmax损失

之——softmax与交叉熵

杂谈

? ? ? ? 我们常用到softmax函数与交叉熵的结合作为损失函数以监督学习，这里做一个小小的总结。

---

正文

1.softmax的基本改进

? ? ? ? 所谓softmax就是在对接全连接层输出时候把输出概率归一化，最基础的就是这样：

? ? ? ? 效果就是这样：

? ? ? ? 数值上达到的效果就是使得最后输出总和为1，范围0~1.

a = np.array([38,20,40,39])
softmax_a = np.exp(a) / np.sum(np.exp(a))
print(softmax_a)
#[9.00305730e-02 1.37116380e-09 6.65240955e-01 2.44728471e-01]

? ? ? ? 但是这个是存在数值不稳定的，极小或极大的差异将会溢出，x很小的都会被归为0，大的又会溢出，所以我们通常做了一定的改进。?

改进一：减去最大防止溢出

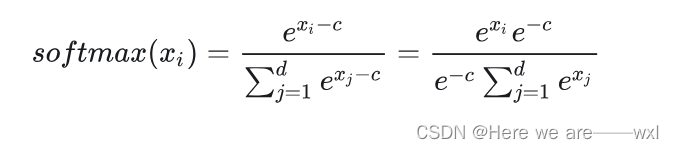
? ? ? ? C一般是我们的数值最大值，这个操作使得我们可以防止x过大的情况出现，减小指数函数输入差异。这只是对运算过程中做一下数值稳定性的规约，不会影响输出结果。

a = np.array([38,20,40,39])
a_max = np.max(a)
softmax_a = np.exp(a-a_max) / np.sum(np.exp(a-a_max))
print(softmax_a)
#[9.00305730e-02 1.37116380e-09 6.65240955e-01 2.44728471e-01]

改进二：Log

? ? ? ? 为了一定程度上消除求幂指数和除法，通常会对以上的softmax取log，这样可以除法转化为减法，，并减少一次幂指数的计算，也提高了梯度的计算能力，甚至跟香农信息熵的形式一定程度地联系了起来。

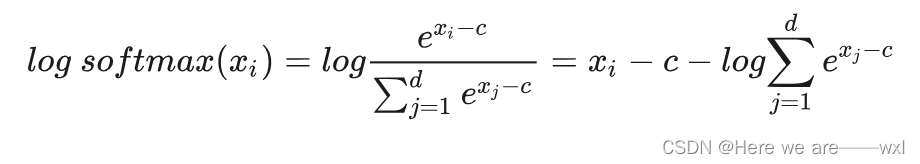
a = np.array([38,20,40,39])
a_max = np.max(a)
time1 = time.time()
for i in range(100000):
    softmax_a = np.exp(a-a_max) / np.sum(np.exp(a-a_max))
    softmax_a = np.log(softmax_a)
time2 = time.time()
print("未优化时间：",time2-time1)
print("softmax_a:",softmax_a)

time3 = time.time()
for i in range(100000):
    softmax_a = a-a_max - np.log(np.sum(np.exp(a-a_max)))
time4 = time.time()
print("优化时间：",time4-time3)
print("softmax_a:",softmax_a)


未优化时间： 0.8376865386962891
softmax_a: [ -2.40760597 -20.40760597  -0.40760597  -1.40760597]
优化时间： 0.7791688442230225
softmax_a: [ -2.40760597 -20.40760597  -0.40760597  -1.40760597]

? ? ? ? ?十万次计算下的速度优化。

改进三：Softmax Temperature

? ? ? ? softmax可能存在对于一些数值上相近的向量数值，概率却相差很大，比如上面接受的输入是[38,20,40,39]，不加log输出就是[0.09, 0.00, 0.6, 0.24]，加log的输出就是[ -2.41 -20.41 ?-0.41 ?-1.41]，可见相差实在是太大了，所以引入一个对于输入范围的缩小，希望输入都在平滑合理的区间内：

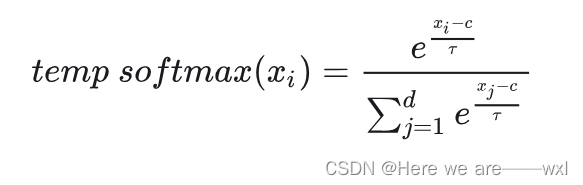
a = np.array([38,20,40,39])
a_max = np.max(a)
tao=100
softmax_a = np.exp((a-a_max)/tao) / np.sum(np.exp((a-a_max)/tao))
print("softmax_a:",softmax_a)

softmax_a: [0.25869729 0.21608214 0.26392332 0.26129724]

? ? ? ? 设置tao为100，可见输出变得更为很合理。

改进四：FC + Softmax——Modified Softmax

????????在很多时候，Softmax接在一个全连接层（或者某个能够统一维度的层）之后,所以形式上改进为：注意，由于这里是矩阵形式的x，所以xi、xj表示的都是那个展平的x，由W的标号决定对应的输出yj：

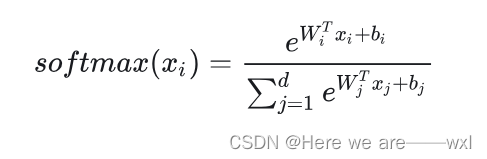
? ? ? ? 消除向量表达全部变为标量那就是modified softmax：

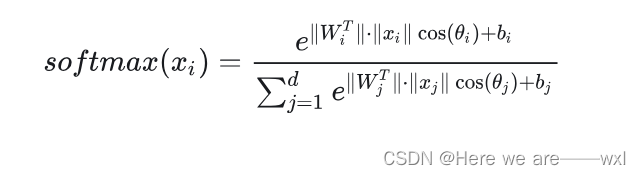
? ? ? ? 如果能将 W=1，b=0，就得到了一个比较规范化的modified softmax：

---

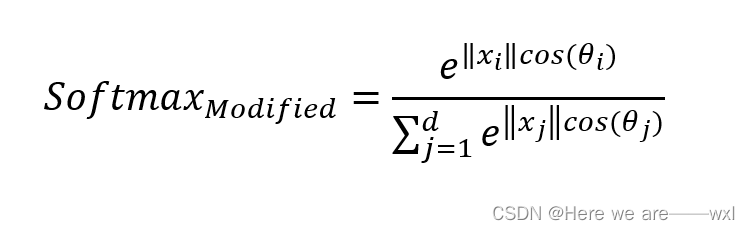
2.softmax的演变

? ? ? ? 数据科学家想要在softmax上面做一些特定性的改变来显式得体现出改进。

演变一：Large-Margin Softmax(L-Softmax)

? ? ? ? 思路是想要在分类任务中，使得类内距离尽可能小，类间距离尽可能大。于是L-Softmax提出基于Modified Softmax增加一个超参数来控制。想要将特征与参数分解为振幅和具有余弦相似度的角：

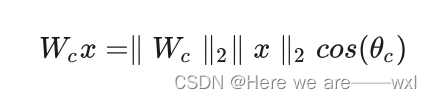
? ? ? ? 如果是个二分类，上文中提到的modified softmax的分类为1类依据是（分母相同，忽略偏差）：

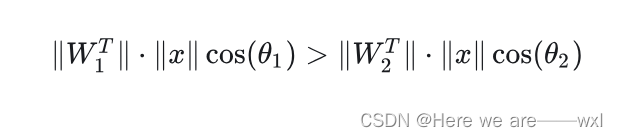
? ? ? ? 而?L-Softmax则类似于间隔化的思想，想要分类更严格并扩大决策范围：(m>=1，0 ≤ θ1 ≤ π/m )

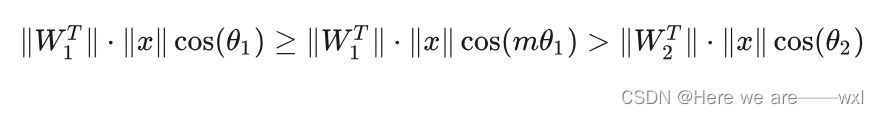
? ? ? ? 那么我们的学习目标就变成了后式，也就是要更严格的θ，也就是相比没有引入m时更小的θ。? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ??

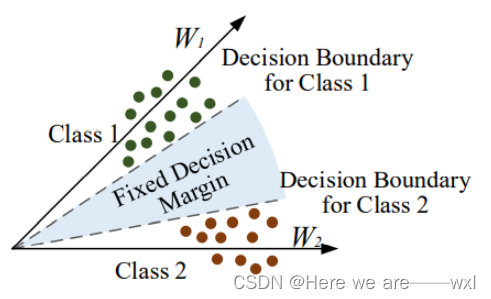
????????因为?m是正整数，cos 函数在?0?到 π?范围是单调递减的，所以 cos(mθ)?要小于 cos(θ)则m要>=1 。 m 值越大则表示我想要的间隔越大，因此通过这种方式调大m定义损失会逼得模型学到类间距离更大的，类内距离更小的特征。?我如果增大m，则表示我要你的θ1更小，意思是最后寻找到的特征空间的类间距离更大的，类内距离更小。当然为了满足学习目标，θ2也会被压小。

? ? ? ? 最终定义为：

? ? ? ? 为了满足分段函数的连续，原文构造了一个函数：

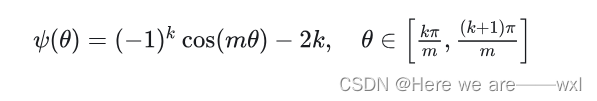
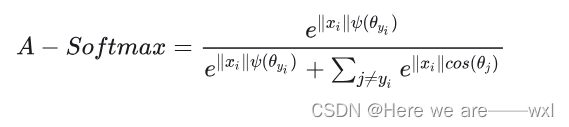
演变二：?Angular Softmax(A-Softmax)

????????A-Softmax的改进思路和L-Softmax相似，都是对于在分类任务中，使得类内距离尽可能小，类间距离尽可能大，只不多A-Softmax与L-Softmaxd区别主要是A-Softmax多了一个权重归一化，和Modified Softmax里面的权重归一化一样：

演变三：?Additive Margin Softmax(AM-Softmax)

????????将L-Softmax & A-Softmax的?改造为新函数：，然后把W和x都归一化，而我们又知道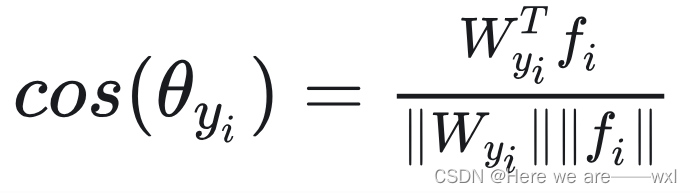：，分母归一化为1了，这样原来的式子就变成了：

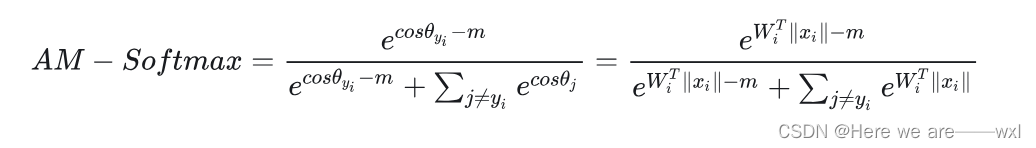
? ? ? ? 直接跟正则化扣上了，我增大m，那模型训练时候为了让softmax大那其Wx就得大，那肯定只能训练出越靠近x的W才会越大啦。这样的好处是求导极其简单。

演变n：还有一堆

Softmax与其变种 - 知乎 (zhihu.com)

---

3.交叉熵

? ? ? ? 交叉熵的引入就是通过独热编码将注意力集中在分类正确的softmax上，用分类正确的softmax的梯度更新权重，因为只有分类正确的-log p*log(q)的p才会是1。

? ? ? ? 而至于说log则达到了我们之前所做的log_softmax的效果，取-就直接表示要最小化损失，最大化softmax输出。

---

感谢：1??2??3??