n-皇后问题——DFS
发布时间:2024年01月23日
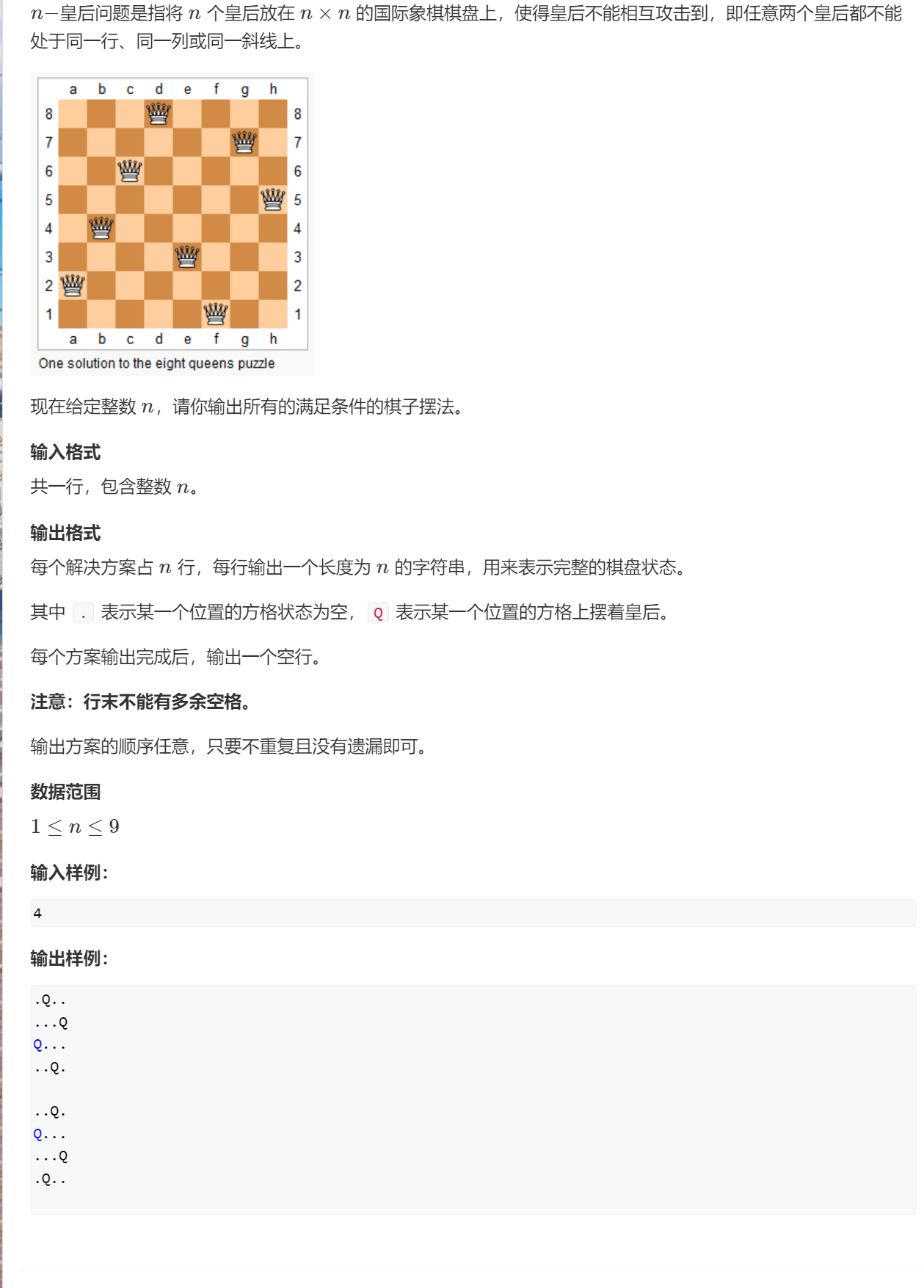
问题描述
第一种方法
- 每一行放一个皇后
- 边放皇后边判断是否符合条件
- 递归到第n行,则说明当前方案符合条件,进行遍历
代码实现
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 10;
int n;
char path[N][N]; // 二维棋盘
bool col[N], dg[N * 2], udg[N * 2]; // col表示列、dg表示对角线、udg表示反对角线
void dfs(int u)
{
if(u == n) // 当前行数等于n,皇后放置完毕
{
for(int i = 0; i < n; i++)
{
for(int j = 0; j < n; j++) cout << path[i][j];
puts("");
}
puts("");
return;
}
for(int i = 0; i < n; i++) // 判断当前行在哪一列放皇后
{
if(!col[i] && !dg[u + i] && !udg[u - i + n]) // 满足条件
{
path[u][i] = 'Q';
col[i] = dg[u + i] = udg[u - i + n] = true;
dfs(u + 1);
col[i] = dg[u + i] = udg[u - i + n] = false; // 回溯
path[u][i] = '.';
}
}
}
int main()
{
cin >> n;
for(int i = 0;i < n; i++) // 初始化
for(int j = 0; j < n; j++) path[i][j] = '.';
dfs(0);
return 0;
}第二种方法
- 遍历每一个位置,分两种情况
- 放皇后
- 不放皇后
- 每次遍历记录当前棋盘上放的皇后的数量
- 当数量等于n时,当前皇后的放置位置符合条件
代码实现
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 10;
int n;
char path[N][N];
bool row[N], col[N], dg[N * 2], udg[N * 2]; // row表示行、col表示列、dg表示对角线、udg表示反对角线
void dfs(int x, int y, int s) // x表示x轴位置,y表示y轴位置,s表示当前棋盘皇后数量
{
if(y == n) // 当y轴超出棋盘范围,x轴加1,y轴为0
{
y = 0;
x++;
}
if(x == n) // 当前位置x轴超出棋盘范围,如果皇后数量为n,当前棋盘满足条件
{
if(s == n)
{
for(int i = 0; i < n; i++)
{
for(int j = 0; j < n; j++) cout << path[i][j];
puts("");
}
puts("");
}
return;
}
// 不放皇后
dfs(x, y + 1, s);
// 放皇后
if(!row[x] && !col[y] && !dg[x + y] && !udg[x - y + n])
{
path[x][y] = 'Q';
row[x] = col[y] = dg[x + y] = udg[x - y + n] = true;
dfs(x, y + 1, s + 1); // y轴加1
row[x] = col[y] = dg[x + y] = udg[x - y + n] = false; // 回溯
path[x][y] = '.';
}
}
int main()
{
cin >> n;
// 初始化
for(int i = 0;i < n; i++)
for(int j = 0; j < n; j++) path[i][j] = '.';
dfs(0, 0, 0); // 从(0, 0)出发,皇后数量为0
return 0;
}
文章来源:https://blog.csdn.net/m0_73197206/article/details/135768416
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!