代码随想录刷题题Day34

刷题的第三十四天，希望自己能够不断坚持下去，迎来蜕变。😀😀😀
刷题语言：C++
Day34 任务
● 198.打家劫舍
● 213.打家劫舍II
● 337.打家劫舍III

1 打家劫舍

198.打家劫舍

思路：
动态规划
当前房屋偷与不偷取决于 前一个房屋和前两个房屋是否被偷了
（1）确定dp数组（dp table）以及下标的含义
dp[i]：考虑下标i（包括i）以内的房屋，最多可以偷窃的金额为dp[i]
（2）确定递推公式
决定dp[i]的因素就是第i房间偷还是不偷
如果偷第i房间，那么$dp[i]=dp[i?2]+nums[i]$
如果不偷第i房间，那么$dp[i]=dp[i?1]$

然后dp[i]取最大值，即dp[i] = max(dp[i - 2] + nums[i], dp[i - 1]);

（3）dp数组如何初始化

vector<int> dp(nums.size());
dp[0] = nums[0];
dp[1] = max(nums[0], nums[1]);

（4）确定遍历顺序

for (int i = 2; i < nums.size(); i++) {
	dp[i] = max(dp[i - 2] + nums[i], dp[i - 1]);
}

（5）举例推导dp数组

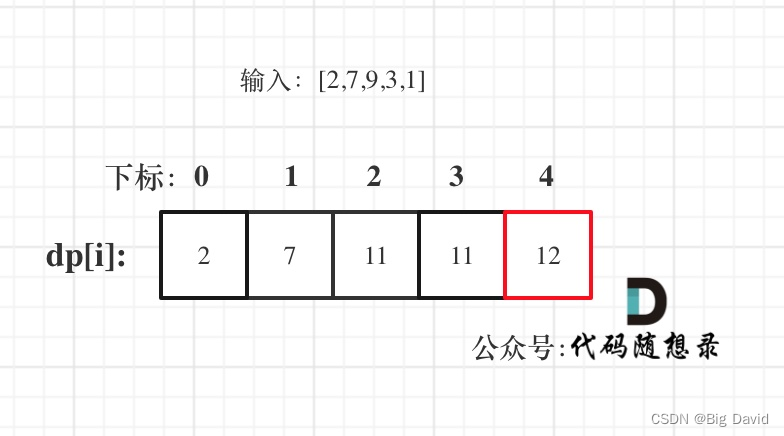
C++：

class Solution {
public:
    int rob(vector<int>& nums) {
        if (nums.size() == 0) return 0;
        if (nums.size() == 1) return nums[0];
        vector<int> dp(nums.size());
        dp[0] = nums[0];
        dp[1] = max(nums[0], nums[1]);
        for (int i = 2; i < nums.size(); i++) {
            dp[i] = max(dp[i - 2] + nums[i], dp[i - 1]);
        }
        return dp[nums.size() - 1];
    }
};

时间复杂度: $O(n)$
空间复杂度: $O(n)$

2 打家劫舍II

213.打家劫舍II

思路：
动态规划
和上一题差不多，区别就在于成环
（1）考虑不包含首尾元素

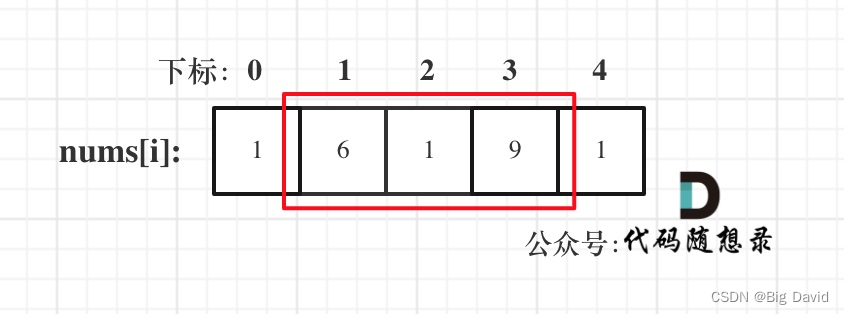
（2）考虑包含首元素，不包含尾元素

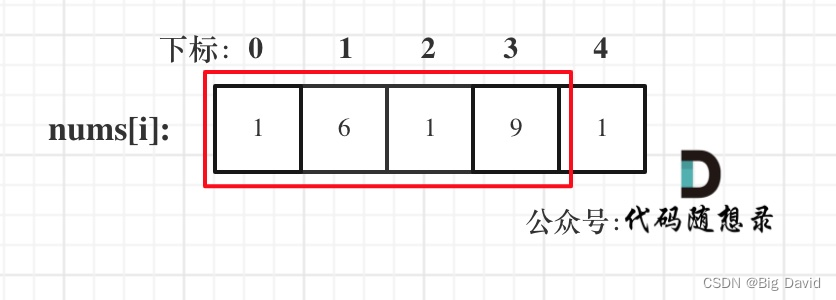
（3）考虑包含尾元素，不包含首元素

C++:

class Solution {
public:
    int rob(vector<int>& nums) {
        if (nums.size() == 0) return 0;
        if (nums.size() == 1) return nums[0];
        int result1 = robRange(nums, 0, nums.size() - 2);// 情况二
        int result2 = robRange(nums, 1, nums.size() - 1);// 情况三
        return max(result1, result2);
    }
    int robRange(vector<int>& nums, int start, int end) {
        if (end == start) return nums[start];
        vector<int> dp(nums.size());
        dp[start] = nums[start];
        dp[start + 1] = max(nums[start], nums[start + 1]);
        for (int i = start + 2; i <= end; i++) {
            dp[i] = max(dp[i - 2] + nums[i], dp[i - 1]);
        }
        return dp[end];
    }
};

时间复杂度: $O(n)$
空间复杂度: $O(n)$

3 打家劫舍III

337.打家劫舍III

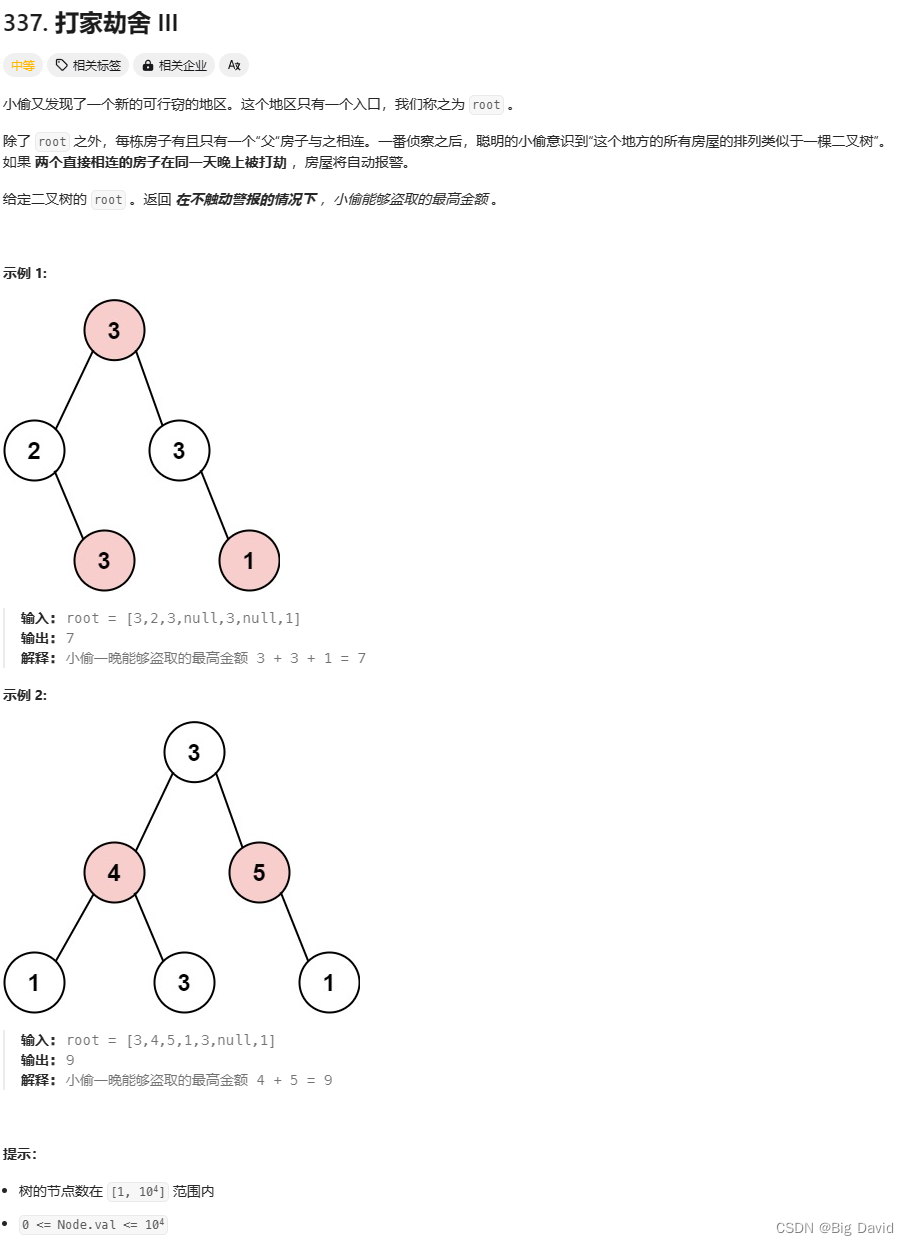
思路：
动态规划+递归

树形dp的入门题目，因为是在树上进行状态转移，以递归三部曲为框架，融合动规五部曲的内容来进行讲解。

（1）确定递归函数的参数和返回值
参数：当前节点
返回值：偷与不偷

vector<int> robTree(TreeNode* cur)

返回数组就是dp数组：下标为0记录不偷该节点所得到的的最大金钱，下标为1记录偷该节点所得到的的最大金钱。
（2）确定终止条件
遇到空节点的话，很明显，无论偷还是不偷都是0

if (cur == NULL) return vector<int>{0, 0};

（3）确定遍历顺序
明确的是使用后序遍历。 因为要通过递归函数的返回值来做下一步计算。

通过递归左节点，得到左节点偷与不偷的金钱
通过递归右节点，得到右节点偷与不偷的金钱

vector<int> left = robTree(cur->left);
vector<int> right = robTree(cur->right);

（4）确定单层递归的逻辑
如果是偷当前节点，那么左右孩子就不能偷
$val1=cur?>val+left[0]+right[0]$
如果不偷当前节点，那么左右孩子就可以偷，至于到底偷不偷一定是选一个最大的
$val2=max(left[0],left[1])+max(right[0],right[1])$
最后当前节点的状态就是{val2, val1}; 即：{不偷当前节点得到的最大金钱，偷当前节点得到的最大金钱}

vector<int> left = robTree(cur->left);
vector<int> right = robTree(cur->right);
// 偷cur
int val1 = cur->val + left[0] + right[0];
// 不偷cur
int val2 = max(left[0], left[1]) + max(right[0], right[1]);
return {val2, val1};

（5）举例推导dp数组

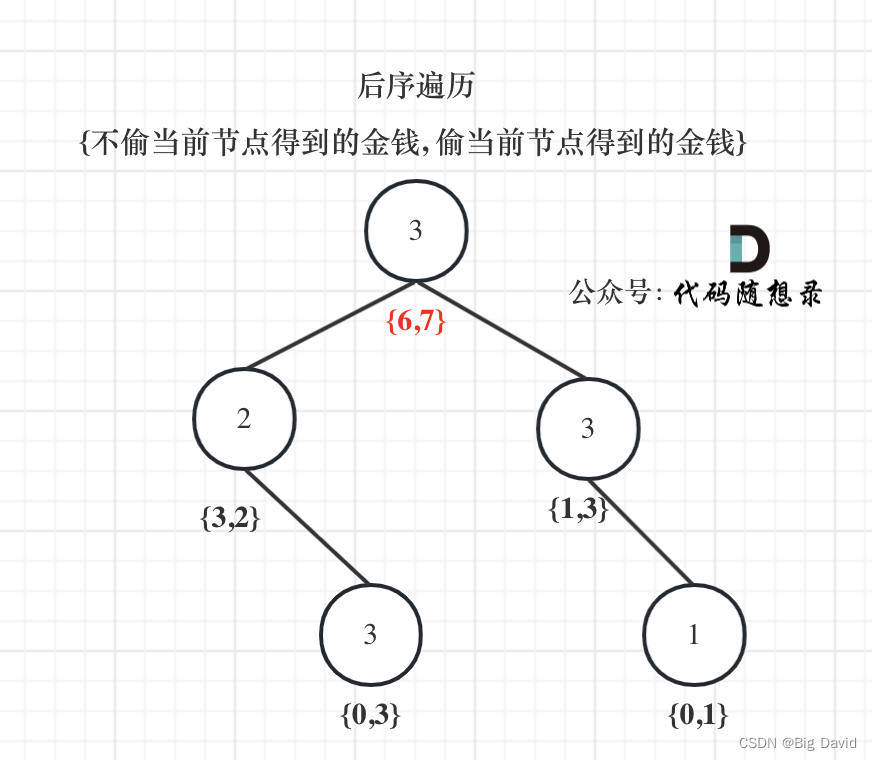
最后头结点就是 取下标0 和 下标1的最大值就是偷得的最大金钱

class Solution {
public:
    int rob(TreeNode* root) {
        vector<int> result = robTree(root);
        return max(result[0], result[1]);
    }
	// 长度为2的数组，0：不偷，1：偷
    vector<int> robTree(TreeNode* cur) {
        if (cur == NULL) return vector<int>{0, 0};
        vector<int> left = robTree(cur->left);
        vector<int> right = robTree(cur->right);
        // 偷cur，那么就不能偷左右节点
        int val1 = cur->val + left[0] + right[0];
        // 不偷cur，那么可以偷也可以不偷左右节点，则取较大的情况
        int val2 = max(left[0], left[1]) + max(right[0], right[1]);
        return {val2, val1};
    }
};

时间复杂度：$O(n)$，每个节点只遍历了一次
空间复杂度：$O(logn)$，算上递推系统栈的空间

---

鼓励坚持三十五天的自己😀😀😀