MATLAB课程第4章的练习题:判断、循环语句相关的题目
题目分为三个部分:
-
基础篇:帮助大家再次复习基础的内容,题目的答案大部分都能直接在本章的知识点中找到。
-
提高篇:在本章课上练习题的基础上进行了一点变形,考验大家对于知识点的熟练程度。这部分的习题不算难,相信大多数的同学都能应对得了。
-
挑战篇:这部分的习题有一定的难度,主要训练大家的编程思维。这部分的习题如果你能独立地做出来,那就说明你非常有编程天赋,大家可以尝试挑战一下。
-
参考答案在本文的最后,有题目的讲解视频。
基础篇
Q1. 填空题
- 在执行循环语句时,如果陷入了死循环,可以按快捷键???????????????? 中断程序的运行;如果要自动整理代码的缩进、对齐等可以选中代码按快捷键 ??????????????????????。
- if后面通常接上关系运算符或逻辑运算符,若为true则执行if后面的语句。如果你在if后面放上了一个矩阵或者向量,这时候只有当这个矩阵或者向量中的元素满足???????????????????????????????????????????????????????? ,才会被当成true。
- 程序可能会面临意想不到的错误或异常情况,如数据输入错误、文件读取问题,我们可以使用 ????????????????????????????????语句捕获和处理异常。
- input函数有两种调用方式,使用 ?????????????????????????????????????????????????可获取纯文本输入。
- 要获取代码的运行时间,我们可以 ???????????????????????????????????????????????????????????????????。
- 代码??????? ?????????????????可以将程序暂停1分钟。
- 和if条件语句配套的剩下三个关键字是 ??????????????????????????????????????????????????????????。
- 和switch条件语句配套的剩下三个关键字是 ??????????????????????????????????????????????????????????。
- 函数 ??????????????????可以将文本、数值等输出到MATLAB的窗口。
- 字符向量使用 ??????????????引起来,字符串使用 ??????????????引起来;比较两个字符向量或者字符串是否相等可以使用函数 ??????????????????。
- 如果不希望看到警告信息,那么可以在运行代码之前先运行 ????????????????????????命令。
- 元胞数组的元素使用 ?????????????括起来;在switch-case语句中,如果case后面是元胞数组,那么当 ????????????????????????????????????????????????????????????????,则为逻辑值1。
- 如果变量x等于eye(3),那么循环语句for ii = x中,进行到第二次循环时变量ii的值是 ????????????????????????。
- 使用循环得到N次模拟结果,并将最终的结果计算平均值来估计期望,这种方法称为 ??????????????????????????????????。
- ?????????????????????函数可用来显示报错信息并终止程序。
- 考虑存在循环嵌套的场景,如果你的代码中用到了两个for循环,且在内层循环中使用了一个break,那么这个break会导致 ??????????????????????????????????????????????。
- 使用warning函数显示警告信息时,后续的语句 ??????????(会/不会)继续运行。
- 如果MATLAB版本较低,使用warning("abc")会报错,应改成?????????????????????????? 。
Q2. 下面这段判断正负数的代码有问题吗?如果有问题应该如何修改?

Q3. 本章4.2.1节中有一个思考题,计算当n从1一直取到100时,下面这个表达式的计算结果:

并将计算结果保存到一个长度为100的行向量S中(S中第i个元素表示y(i)的结果)。我们课堂上给出的代码是:
S = zeros(1, 100);
for n = 1:100
y = 0; % 初始化y的值为0
for k = 1:n
y = y + 1 / (k^2);
end
S(n) = y;
end
disp(S)
请回答:(1)y = 0;这行代码能否放在循环的外面? (2)能否优化上面的代码,只循环一次就得到S。(3)能否使用第三章的知识,不使用循环直接计算S。
Q4. 给定一个包含3个元素的行向量a,使用if语句对向量a中的元素按照从小到大的顺序排序,并将排序后的向量保存到sort_a中。例如原来a=[3,8,5],那么sort_a=[3,5,8]。(你可以使用循环重复运行你的代码100次,每次生成的a都是随机的,测试你的代码是否有问题)
Q5. 本章4.2.3节中,有一道判断n是否是质数的例题。当时的思路是遍历从2到n-1的所有整数,检查它们是否能够整除n。如果找到任何一个能够整除n的整数,那么n就不是质数;否则,n就是质数。事实上我们可以缩小循环遍历的范围来提高效率。一般来说,只需要检查从2到n的平方根(如果为小数则需要向上取整)之间的整数,原因是如果n有一个大于sqrt(n)的因子,那么它必定有一个小于sqrt(n)的因子。请解决下面两个问题:(1)优化遍历的范围,对于n=100000037,比较优化前后的代码的运行时间;(2)自然数2至10000中的质数有哪些?(注意2也是质数,需要单独判断)。
Q6. 下面这两段代码输出的结果分别是什么?

Q7. 一个五位正整数各位数字的五次方和等于该数本身则称该数为五角星数,请找出所有的五角星数并将其保存到向量S中。
Q8. 生成一个8行5列的矩阵,矩阵中每一个元素都是在区间[1,10]上取值的随机整数。接下来请循环每一行,若发现同一行的五个元素中各不相同,则保留该行。
Q9. 在本章介绍break和continue的小节中,有一道和斗地主相关的例题。请使用蒙特卡罗模拟计算你作为农民首次出现炸弹所需的轮数的期望值。
Q10. a和b是用户输入的两个常数,如果用户输入“乘法”这个文本,则输出a×b;若用户输入“除法”这个文本,则先判断 b 是否为0,若为0则生成错误信息:分母不能为0,否则输出a/b;如果输入的是其他的文本,则生成警告信息:只能输入乘法或除法。
提高篇
Q1. 一张100元的人民币要换成10元、5元和1元面值的零钱,要求三种面值的零钱的总张数为20张,且三种面值至少都有一张,用一个矩阵表示所有可能的组合,矩阵中每一行的三个元素分别表示三种面值人民币的张数(例如8? 2? 10三个元素就是矩阵的某一行)。
Q2. 假设自然界中有一种动物,它每天被天敌捕食的概率均为0.02,且每天是否被天敌捕食这个事件是独立的。请使用蒙特卡罗模拟得到这种动物能存活的天数的期望值。
Q3. 一个班上有30名同学,请使用蒙特卡罗模拟计算至少有两人是同一天生日的概率。
Q4. 每隔0.2秒在屏幕上随机输出0或者1,当连续出现三次1时,停止输出。
Q5. 扔一枚正常的硬币,若要扔出连续的3个正面,所需扔硬币的期望次数是多少?请使用蒙特卡罗模拟进行计算,精确的数学答案是14。
Q6. 有三个长度均为10的向量,分别是r = [5 3 2 2 4 1 3 5 1 4]、c = [3 4 1 2 5 5 2 4 4 2 ]、x = [9 6 3 7 5 1 4 9 2 4],若A矩阵是一个元素全为0的5阶方阵。请根据r、c和x三个向量给A矩阵重新赋值:将x(i)赋值给A中第r(i)行、第c(i)列的元素(i=1,2,?,10)。另外,大家可以思考能否不使用循环语句得到A矩阵?最终得到的A矩阵供大家参考:

Q7. 随机生成一个各行各列的和均为1的5阶方阵,且该方阵的元素仅为0或1。例如下面这个矩阵就符合要求。(大家也可以尝试不使用循环语句得到这个随机的方阵)
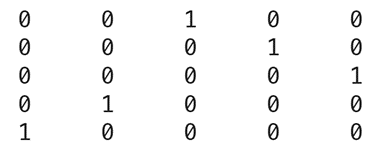
Q8. 将一根长度为1米的木棍随机的折成三段,请用蒙特卡洛模拟分别计算以下两个概率:(1)每段长度都不大于0.45的概率;(2)这三段能构成一个三角形的概率。
Q9. 一只蜗牛从10米深的井底往上爬,它白天爬1米,晚上下落x米,其中x为[0,2]米的均匀分布的随机数,求它爬出这口井的期望天数?本题选自知乎,精确答案约为277天。
Q10. 给定一个1到1亿之间的整数,请判断这个整数是否为回文数(反向排列与原来一样的数就叫做回文数。如:1、353、4774都是回文数)。
Q11. 二分搜索法不仅可以用于求函数的零点,还可以用于寻找向量中的特定值。给定一个长度为100且递增排列的向量x和一个要查找的目标值t,使用二分搜索法确定向量x中是否存在目标值t。请回答下面两个问题:(1)为了方便,你可以使用下面两句代码随机生成x和t:x = sort(randi(200,1,100));? t = 88; 若x中存在多个t,你只需要返回任意一个t的下标,如果不存在t请返回0。(2)假设我们令x = sort(randi(30,1,100));? t = 8,那么x中出现多个t的次数将大大增加。请在上一问代码的基础上进行调整,使得代码能够输出t所在的所有下标,如果找不到t请返回空向量[ ]。(你可以和find函数找到的结果进行比较:find(x == t),看看结果是否一致)
Q12. 有一个人从原点(第0格)开始扔一个六面骰子(骰子数值为1-6),扔到几就向前走几格,假设他可以无限次扔骰子,问他恰好走过第100格的概率是多少? 这个题目选自知乎,精确答案约为2/7。
Q13. 编写一个猜数游戏的代码,规则如下:在区间[1,100]上随机生成一个整数p,用户需要去猜这个p是多少。用户每猜一次程序都会做出相应的提示“请输入你猜的数字:”。若用户输入所猜的数字小于p,则提示“你猜小了!”;若大于p,则提示“你猜大了!”;若相等,则提示“恭喜你赢了!”,游戏结束。用户猜的次数不能超过六次,否则提示“最多猜六次,你失败了。”,此时游戏结束。
Q14. 知乎上有这样一个问题:

请使用蒙特卡罗模拟验证这个答案是否可行(假设有30个人玩这个游戏)。
Q15. 下面这题来自2022年阿里巴巴全球数学竞赛,请大家求解该题。

挑战篇
Q1. 排序算法是一类经典的算法,它们能将一个无序的向量变成有序的向量。请大家在网上搜索插入排序、选择排序和冒泡排序的讲解视频或者文字资料,并使用MATLAB复现这三种算法。为了测试方便,你可以令x=randi(100,1,20),将x中的元素按照从小到大进行排序。若你的代码返回的结果和sort(x)的结果相同,则说明你做对了。(如果你看懂了算法原理也写不出来代码的话,可以参考这三种算法的伪代码)
附:三种排序算法的伪代码
伪代码(Pseudocode)是一种描述算法的语言,它介于自然语言和编程语言之间。使用伪代码的目的是使被描述的算法可以容易地以任何一种编程语言(C、Java、Python等)实现,因此伪代码必须结构清晰、可读性好。
下面给出了挑战篇Q1中三种排序算法的伪代码。为了帮助大家理解,我在伪代码中加上了注释。另外,下面给出的伪代码中的循环、判断语句没有以end结尾,大家需要自己根据代码的缩进来判断end的位置。



Q2. 在MATLAB中,'parfor'(Parallel for)是一种并行编程工具,它允许在多个处理核心上同时执行循环迭代。这种方法与常规的for循环类似,但能够在多个工作进程上并行执行循环迭代,从而加快代码运行速度。这对于需要进行重复计算或处理大型数据集的任务尤为有效。请在MATLAB官方网站上搜索关于'parfor'的相关信息,并尝试将之前代码中的for循环替换为parfor循环。测试代码是否能够正常运行,并比较for循环和parfor循环的执行时间。
Q3. 某游戏中有一把武器,该武器的初始等级为1级,在游戏开始时玩家可以免费领取。在游戏中,玩家可以花费金币对该武器进行升级,每次升级需要花费10000金币,且该武器最多能被升至5级。各等级升级的成功率如下表所示:

以等级1和等级3所在的行为例,表格中各元素的解释如下:
- 1级武器升级时,有20%的概率升到2级,10%概率升到3级,5%的概率升到4级,65%的概率不变。
- 3级武器升级时,10%概率跌到1级,20%概率跌到2级,20%概率升到4级,10%概率升到 5 级,40%的概率不变。
请使用蒙特卡罗模拟,计算打造一把5级的武器平均需要花费多少金币(答案约16万)。
Q4.在一台设备上,安装有四只型号和规格完全相同的电子管。假设这些电子管的寿命是整数小时,且在1000至2000小时之间均匀分布。设备运行中若出现电子管损坏,有两种维修方案可供选择:(1)逐个更换方案:每次只更换损坏的那一只电子管,更换单个电子管需要1小时的时间;(2)集体更换方案:当任意一只电子管损坏时,同时更换所有四只电子管,一次性更换四只电子管需要2小时的时间。已知每只电子管的价格为100元,且不论采用哪种维修方案,设备在更换电子管期间都需要暂停运转,导致的损失为每小时200元。请使用蒙特卡罗模拟判断选择哪一种维修方案更省钱(你可以设置总的模拟时长为10万小时,比较该设备运行10万小时后,哪种方案花费更小。参考答案:方案二比方案一节省约1.3万)
Q5. 三门问题(Monty Hall problem)又称蒙提霍尔问题或蒙提霍尔悖论,它是一道非常有趣的概率问题,该问题的答案违反大家的直觉。请大家搜索三门问题的相关资料,并使用MATLAB验证三门问题的答案(更换门的概率更高为2/3)。
Q6. 莱斯利矩阵是英国生态学家Leslie于1945年提出的一种数学方法,该方法能利用某一初始时刻种群的年龄结构现状,动态地预测种群年龄结构及数量随时间的演变过程。请大家查阅相关资料学习该模型的建模过程,并解决下面这个问题。
已知某动物最长寿命为10岁,且初始状态下该动物各年龄组的数据如下表所示:

表中雌性生育率解释为雌性个体在一个繁殖周期内平均产生的后代数量(包括雄性和雌性)。假设该动物繁衍过程满足以下条件:1. 该动物在各个年龄段的雌雄比例都是2:1;2. 新出生注意的该动物的雌雄比例也是2:1;3. 各年龄组内该动物的生育率和死亡率不随时间变化。
请回答以下问题:(1)预测该动物未来30年各年龄段的数量以及占比(参考答案:30年后0岁数量为687846);(2)若该动物的天敌在第30年后开始出现,这将导致从下一年开始各年龄段的死亡率均增加到原来的三倍,雌性生育率也降低到原来的一半。请问该动物从遭遇天敌开始,需要多少年该动物的数量会下降到1000只内。(参考答案:42年)
Q7. 本题节选自2023年阿里巴巴全球数学竞赛,题目如下:A与B二人进行“抽鬼牌”游戏。游戏开始时,A手上有n张两两不同的牌。B手上有n+1张牌,其中n张牌与A手中的牌相同,另一张为“鬼牌”,鬼牌与其他所有的牌都不同。游戏规则为:
- 双方交替从对方手中抽取一张牌,A 先从B手中抽取。
- 若某位玩家抽到对方的牌与自己手中的某张牌一致,则将两张牌丢弃。
- 最后剩一张牌(鬼牌)时,持有鬼牌的玩家为输家。
假设每一次抽牌从对方手上抽到任一张牌的概率都相同,请用蒙特卡罗模拟n分别为31和32时,A 获胜的概率。(参考答案:n=31时为17/33,n=32时为9/17)。
Q8. 这是一道排队论的题目。假设某银行工作时间内只有一个服务窗口,工作人员只能逐个接待客户。当来的客户较多时,一部分客户就需要排队等待。若假设以下四个条件成立:(1)从银行开始营业起,客户到达的间隔时长(单位为分钟)服从参数 λ?等于0.1的指数分布;(2)每位客户的服务时长服从均值为10,方差为4的正态分布(单位为分钟,若服务时长小于1分钟,则按1分钟计算);(3)排队按先到先服务的规则,且不限制队伍的长度;(4)银行每天工作时长为8小时,若客户开始服务的时间比银行下班的时间晚,银行不提供服务。
模拟100个工作日,计算银行平均每天服务的客户人数以及客户的平均等待时长。
Q9. 在上一题的基础上,解决以下三个进阶的问题:
(1)由于客户反馈排队等待时间过长,银行决定开设一个新的服务窗口。请计算在有两个服务窗口的情况下,这100个工作日内银行平均每天服务客户的人数以及客户的平均等待时长。为了简化模拟过程,假设银行采取先到先服务的策略,只要有窗口空闲,就给先来排队的客户提供服务(类似于先取号再叫号的策略)。(2)假设银行新设立的第二个窗口每天仅在前四个小时提供服务(如果客户在后四小时到达银行,则只能去第一个窗口),请重新计算上述问题。(3)请将第1小问的两个窗口推广至p(p≥3)个窗口,并求解相同的问题。
参考答案:
??点击下方的CSDN专栏阅读下一篇文章:
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- leetcode hot 100
- HubSpot线索管理系统怎么样?适合哪些企业?
- linux环境seatunnel安装运行
- 金南瓜SECS/GEM发送event、VID
- Android Studio下载gradle反复失败
- Python数据挖掘与机器学习实践技术应用
- uniapp Vue3 日历 可签到 跳转
- Gateway No servers available for service
- 基于ts+hooks完全实现的移动端组件库
- 【unity小技巧】两种办法解决FPS游戏枪或者人物穿墙穿模问题