数据结构：二叉树

目录

1.树的定义

2.二叉树

2.1 满二叉树

2.2 完全二叉树

2.3 二叉搜索树

2.4 平衡二叉搜索树

3.二叉树的存储

3.1 数组存储

3.2 链表存储

? ? ? ?代码：

4.二叉树的遍历

4.1 深度优先遍历

4.1.1 递归

4.1.2 迭代

4.2 广度优先遍历(层序遍历)

---

1.树的定义

? ? ?树是计算机数据存储的一种结构，因为存储类型和现实生活中的树类似而被称为树。

? ? ?树的源头称为根，其余分叉点称为节点，而起始的分叉点被称为根节点，树的尽头是叶，我们称之为叶节点。

? ? ?每一个节点的起点被称为父节点，由父节点衍生出去的节点称为子节点，没有父节点的节点为根节点，没有子节点的节点称为叶节点，共用一个父节点的节点为兄弟节点。

? ? ? ? ? 树的高度从下往上看，深度则是从上往下看，层数等于高度+1。

2.二叉树

? ? 二叉树是最常见的树形结构，每个节点最最多只能有两个子节点。

? ? 二叉树分为好几种：

2.1 满二叉树

? ? ?如果一棵二叉树只有度为0和度为2的节点，且度为0的节点都在同一层，这样的树就是满二叉树。

2.2 完全二叉树

? ??

在完全二叉树中，除了最底层的节点的子节点数不全为2之外，其余每层每个节点的子节点数都为2，并且最底层的节点集中在该层最左边的位置。就像这样：

2.3 二叉搜索树

? ? 满二叉树和完全二叉树都是没有数值的，二叉搜索树就有数值了，它是一棵有序树。

? ? 如果它的左子树不空，则左子树所有节点的值都小于它的根节点的值；

? ? 如果它的右子树不空，则右子树所有节点的值都大于它的根节点的值；

? ?它的左右子树叶都是二叉搜索树?

2.4 平衡二叉搜索树

? ? ?二叉搜索树前面加了平衡两个字，它是一棵空树或者它的左右两个子树的高度差的绝对值不超过1，并且左右两个子树也是平衡二叉搜索树，这样的树就是平衡二叉搜索树，又被称为AVL(Adelson-Velsky and Landis)树。

? ? ?上图的二叉搜索树是平衡二叉搜索树，但这棵树因为左右两棵子树的高度差超过了1，而不能是平衡二叉搜索树。

3.二叉树的存储

? ? ?二叉树一般有数组和链表两种存储方式，一个是顺序存储，一个是链式存储。

3.1 数组存储

? ? ? 当我们遍历时，如果父节点的数组下标是i，那么它的左子节点就是i*2+1，它的右子节点就是i*2+2。这种方式对于树来说还是不够直观，我们一起来看看链表存储

3.2 链表存储

? ? ? 这种存储方式才能更直观的体现出二叉树的特点，接下来所有的讲解都会使用链表存储，来帮助我们更好的理解。

? ? ? ?代码：

typedef struct TreeNode
{
	int data;
	TreeNode* left;//left指针指向左子节点
	TreeNode* right;//right指针指向右子节点
}TreeNode;

4.二叉树的遍历

? ? 二叉树的遍历主要为两种：

? ? ? ? 深度优先遍历：往深了走，遇到叶节点往回走，通常是递归法。

? ? ? ??广度优先遍历：一层一层地遍历。

? ? 深度优先遍历又分为：前序遍历，中序遍历，后序遍历

? ? 广度优先遍历：层次遍历

4.1 深度优先遍历

? ? ? 这里的前序，中序，后序就是中间节点的位置，前序是中左右，中序是左中右，后序就是左右中。

? ? ?在实现深度优先遍历时，我们经常使用递归的方式，因为我们一直走到头，很符合递归的特点，我们也知道栈其实就是用来实现递归的，所以我们也可以用栈来实现。

4.1.1 递归

? ? ?递归通常从三方面来考虑：

1.确定递归函数的参数和返回值：知道哪些参数是递归过程中需要处理的，就在参数里面加上，并且还要确定递归函数的返回值，确定返回类型
2.确定终止条件：函数不能一直递归下去，这会导致爆栈，所以我们要正确的认识递归的终止条件
3.确定单层递归的逻辑：就是确定每一层递归需要处理什么，重复调用这个过程，达到代码量少却操作很多的目的

? ? ?从前序遍历来看：

? ? ?1.确定递归函数的参数和返回值：因为我们要打印出前序遍历节点的值，所以参数里需要传入vector来存储每个节点的数值，不需要任何返回值

void TravelTree(TreeNode* cur,vector<int>& vec)

? ? ?2.确定终止条件：什么时候递归才能结束呢？我们一直往深走，一直走到一个节点，它没有子节点了，不能再走了，这时候递归就结束了，所以如果当前遍历的节点为空，就return。

if(cur==NULL)return;

? ? 3.确定单层递归的逻辑：因为前序遍历是中左右，所以我们要先取中间节点的数值。

vec.push_back(cur->val);
TravelTree(cur->left,vec);
TravelTree(cur->right,vec);

? ? ?完整代码：

void TravelTree(TreeNode* cur,vector<int>& vec)
{
   if(cur==NULL)return;
   vec.push_back(cur->val);
   TravelTree(cur->left,vec);
   TravelTree(cur->right,vec);
}

? ? ?写出来前序之后，中序和后序就容易了

? ? ?中序遍历：

void TravelTree(TreeNode* cur,vector<int>& vec)
{
   if(cur==NULL)return;
   TravelTree(cur->left,vec);
   vec.push_back(cur->val);
   TravelTree(cur->right,vec);
}

? ? ?后序遍历：

void TravelTree(TreeNode* cur,vector<int>& vec)
{
   if(cur==NULL)return;
   TravelTree(cur->left,vec);
   TravelTree(cur->right,vec);
   vec.push_back(cur->val)
}

4.1.2 迭代

? ? 前序遍历是中左右，每次先处理中间节点，那我们可以先把根节点放入栈中，因为栈是一种先进后出的结构，所以要实现前序遍历，要先把右子节点放入栈中，再把左子节点放入栈中。

vector<int> preorderTravelTree(TreeNode* root)
{
  stack<TreeNode*>st;
  vector<int>vec;
  if(root==NULL)return vec;
  st.push(root);
  while(!st.empty())
  {
    TreeNode* node=st.top(); //中
    st.pop();
    vec.push_back(node->val);
    if(node->right)st.push(node->right); //右
    if(node->left)st.push(node->left);//左
  }
  return vec;
}
    

? ? 后序遍历：前序遍历是中左右，我们可以调整为中右左，最后反转数组就是左右中了

 vector<int> postorderTraverTree(TreeNode* root) {
        stack<TreeNode*> st;
        vector<int> result;
        if (root == NULL) return vec;
        st.push(root);
        while (!st.empty()) {
            TreeNode* node = st.top();//中
            st.pop();
            vec.push_back(node->val); 
            if (node->left) st.push(node->left); //左 相对于前序遍历，这更改一下入栈顺序 
            if (node->right) st.push(node->right); //右
        }
        reverse(vec.begin(), vec.end()); // 将结果反转之后就是左右中的顺序了
        return vec;
    }

? ? 为什么我跳过了中序遍历呢？因为它很特殊，不是简简单单把前序遍历的代码改了就行

? ? 前序和后序遍历都需要先处理中间节点，我们也是先访问中间节点，顺序是一致的，那中序遍历就不是这样了，我们先访问的不是中间节点，这样顺序就不一样了。

? ? 我们需要指针的遍历帮助访问节点，栈处理节点上的元素。

vector<int> inorderTravelTree(TreeNode* root)
{
   vector<int>vec;
   stack<TreeNode*>st;
   TreeNode* cur=root;
   while(cur!=NULL||st.empty())
   {
      if(cur!=NULL)
      {
         st.push(cur);
         cur=cur->left;//左
      }
      else
      {
        cur=st.top();
        st.pop();
        vec.push_back(cur->val);//中
        cur=cur->right;//右
       }
    }
    return vec;
}

4.2 广度优先遍历(层序遍历)

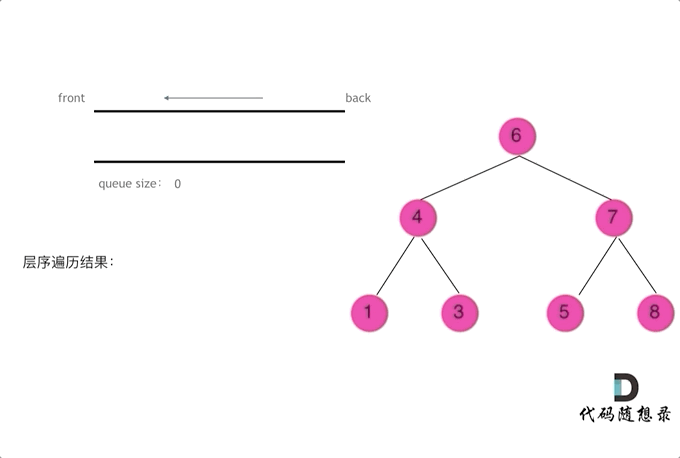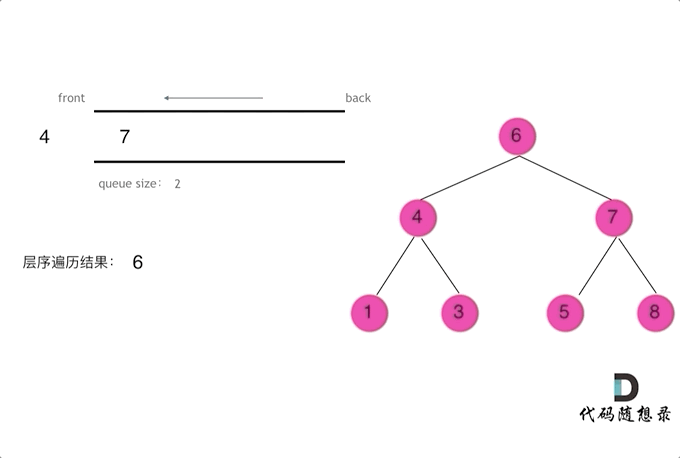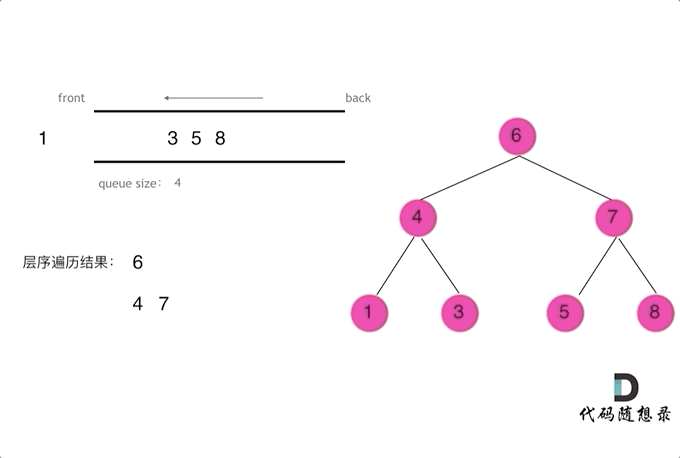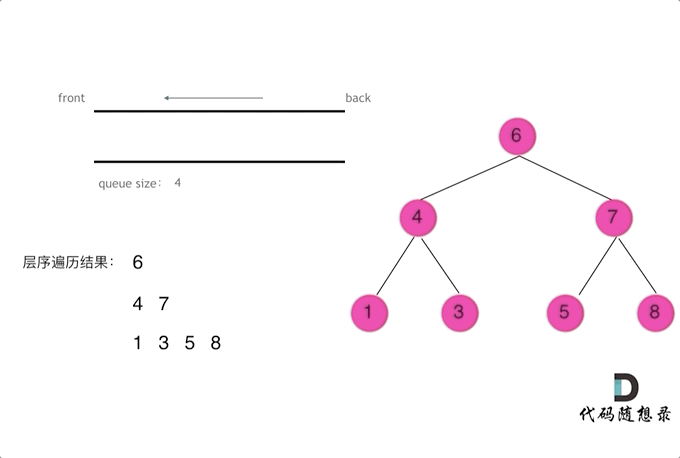
? ? ?层序遍历一个二叉树，就是从左到右一层一层去遍历，队列先进先出，符合一层一层遍历的逻辑。这里借用代码随想录的动画帮助理解

?

? ? ?

vector<int> levelOrderTravel(TreeNode* root)
{
   queue<TreeNode*>que;
   if(root!=NULL)que.push(root);
   vector<int>vec;
   while(!que.empty())
   {
     int size=que.size();
     //不要用que.size(),因为在不断变化
     for(int i=0;i<size;i++)
     {
       TreeNode* node=que.front();
       que.pop();
       vec.push_back(node->val);
       if(node->left)que.push(node->left);
       if(node->right)que.push(node->right);
     }
   }
   return vec;
}