An efficient path-based approach for influence maximization in social networks

?ABSTRACT

??口碑对社会联系的影响非常强大，这已不是什么秘密，但问题是“哪些因素影响口碑的有效性？”答案取决于一小组节点如果被激活，就会将信息传播到整个网络。这是社交网络分析中的一个主要问题，称为影响力最大化，通过一小组种子节点传播的影响力被最大化。由于影响力最大化问题的非确定性多项式时间（NP）困难性质以及社交网络规模的显着增加，找到这种具有高度影响力的节点集仍然具有挑战性。因此，本文提出了一种有效的基于路径的算法，从两个互补的角度来解决这个问题，使所提出的算法适用于大规模网络。一种观点是使用节点的两个特征来有效地近似影响力传播：度数和独立影响路径。第二个角度是使用实用的预处理启发式方法修剪掉无影响力的节点并减少近似影响力传播的计算量。进行了大量的实证实验来评估所提出的算法在七个现实世界网络中的性能，并将结果与??大量最先进的算法进行了比较。结果表明，所提出的算法在质量和效率之间提供了出色的权衡，优于同类算法。

1.Introduction

? ?随着通信技术的发展和互联网应用的普及，社交网络用户的数量呈不断增加的趋势。在线社交网络已成为每个用户日常生活中不可或缺的一部分。因此，每天，大量的信息和想法在网络中交换，可以在短时间内影响大量的人（Tong et al., 2017）。近年来，社交网络之间的影响和信息传播已成为许多研究人员的主要关注点，他们的发现为病毒式营销等不同的在线应用铺平了道路（Wang et al., 2017）。

? ?病毒式营销是一种成功的技术和实用平台，作为发射台，通过在线社交网络的口碑传播。口碑是传统且最实用的营销形式之一，是一种在人们内部传达广告或促销信息的简单方式。为此，假设一家商业公司开发了一种有效的清洁、消毒和消毒工具，因为由于新冠病毒 (COVID19)，他们比以往任何时候都更加重视清洁。该公司希望通过社交媒体营销其新产品。它有有限的预算来选择一些早期用户并鼓励他们（通过赠送礼物或免费出售）使用该工具。公司希望用户接受新产品并开始通过通过社交网络;因此，金字塔结构和朋友会将其传递给他们的朋友的朋友。至于口碑的力量，这是一种非循环的过程，大多数人相信来自自己同类的推荐，这就提出了一个问题：

如何找到最终影响大量用户的初始用户群？

这个问题是影响力最大化问题（IMP）的核心，也是社交网络领域众多研究者关注的焦点。给定图 G、用户影响概率和常数 k，IMP 寻求在图 G 中找到 k 个有影响力的节点，以基于预定义的扩散模型最大化影响扩散 (IS)（Liu 等人，2014）。第一项研究是离散优化问题（Kempe et al., 2003），他们揭示了 IMP 是一个 NP 难问题，受独立级联 (IC) 和线性阈值 (LT) 的影响楷模。他们提出了一种贪心爬山的方法来解决这个问题。在他们的贪婪方法中，应用了蒙特卡罗模拟，这使得计算过程变慢。这种贪婪方法没有应用网络的拓扑特性，因此它在大规模网络中不是一种实用的方法。为此，进行了许多研究来克服原始贪心算法的低效率。 (Bozorgi et al., 2016; Goyal, Lu, & Lakshmanan, 2011b; Heidari et al., 2015; Leskovec et al., 2007; Rostamnia & Kianian, 2019) 提出的算法要么是启发式的，要么是对原始贪婪方法的改进，比第一种方法更快，但不可扩展。为了克服这个缺点，Hieidari 等人。提出了一种可扩展的贪婪算法，其中应用了 Monto-Carlo 模拟，但仍然很耗时（Heidari 等人，2015）。 (Kim et al., 2013) 针对独立级联模型提出了一种可扩展的影响近似算法 IPA，该算法针对独立影响路径评估和近似影响。该方法在一定程度上改善了贪心法的时间消耗。他们通过随机游走查找和分离（修剪）无影响的节点来改进 IPA（Kim 等人，2017）。

? ??关于IPA概念，这里为IC模型提出了一种高效的启发式独立路径算法（HIPA），该算法也是可扩展和可并行的。 HIPA 涉及三个关键思想，通过提高时间复杂度同时保持效率来实现其目标。 HIPA 的第一个特点是应用顶点覆盖算法作为网络的预处理，使算法能够通过从有影响力的节点选择域中删除无用的节点来减少计算操作的数量。 HIPA的第二个特点是通过应用节点之间的路径数量来近似影响力传播，这需要大量的内存来保存路径。 HIPA采用适当的结构来保存路径以降低空间复杂度。第三个特征是将程度启发式和影响力路径结合起来，以实现更准确的影响力近似。

简而言之，这里的贡献是：

1. 为 IMP 提出的一种高效、可扩展且可并行的算法，名为 HIPA.

2. HIPA 在预处理步骤中成功删除了无用节点，从而降低了查找有影响力节点的计算成本

3. HIPA 比许多最近引入的算法更快算法。在IPA、RWP-IPA和TwoHop上进行实验，并将获得的结果与(Kim et al., 2013, 2017; Tang et al., 2018)的结果进行比较，证明了这里的结果。

4.HIPA提供了IS的精确近似，使算法比同类算法表现更好.

本文的其余部分如下：背景和相关工作在第 2 节中介绍；第 3 节介绍了 HIPA 算法；第 4 节介绍了真实数据集的结果，第 5 节对本文进行了总结。

2.Problem formulation

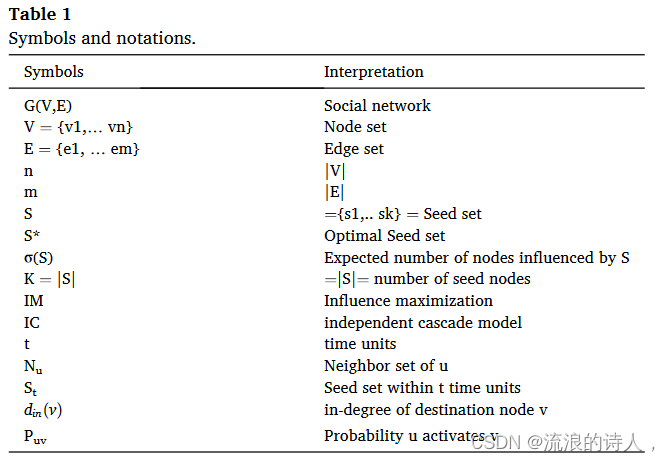
??影响最大化作为一个经典的网络问题，首先被 Kempe 等人格式化为离散优化问题的形式。 (2003)并已被证明是一个NP难题。社交网络被建模为加权有向图 G(V, E, W)。 V 表示引入网络成员的一组节点，其大小等于 (|V| = )n E 是一组大小为 |E| 的边。 =m 表示节点之间的连接。最后，W 是影响权重 puv ε [0, 1] 的集合，它也被分配给每条边 ( u, v) ε E 来表示节点 u 影响节点 v 的概率。关于最大化影响力传播，重要的是要了解影响力如何在社交网络中传播。

现实世界中影响力传播有两个方面：

? 正面及负面。也就是说，发布评论和广告既是为了说服，也是为了劝阻。在不牺牲所提出的 IM 方法的通用性的情况下，本文研究了正独立级联 (IC)1 模型。 IC模型是一种逐一解离模型，节点只有两种状态，活跃或不活跃。给定种子集 S0 ?V，影响力开始以 St?V 是时间步 t 处的一组活动节点的方式传播。如果在步骤 t 没有节点激活，则该过程将终止。在时间步 t 中，根据传播模型给出的概率，只有在时间 t-1 激活的节点才能激活其邻居。 IC 模型中的一个要点是，对于每个节点来说，只有一次机会激活其尚未启用的邻居；这意味着活动节点 u ∈ St 对步骤 t + 2 没有影响并保持其状态。

??独立级联模型有两个重要的系列。在简单 IC 模型的情况下，每个新激活的节点 u 将以固定的预定义概率 p 成功激活每个不活动的邻居 v ∈ Nu。第二个是加权 IC 模型，其中每条边 (u, v) 都有权重 Puv，表示节点 u 激活节点 v 的概率。估计概率 Puv 的一个著名关系是 1 din (v)，其中 din(v) 是目标节点 v 的入度（Shang 等人，2017）。

考虑到种子集 S 是级联过程开始时的一组初始活跃节点，σ(S) 是预期受 S 影响的节点数。正式地，影响最大化问题定义如下：

给定一个具有影响力传播模型和整数 k 的图 G，影响力最大化问题旨在找到种子集 S*? V 且 |S*| ? k 最大化影响范围 σ(S*)，如式（1）所示。 (1).

肯佩等人。 (2003) 证明了 σ(?) 函数既是次模函数又是单调函数。因此IMP可以通过简单的贪婪方法来近似，但该算法非常耗时。表 1 总结了本文本节中使用的符号和符号。

3.Related works

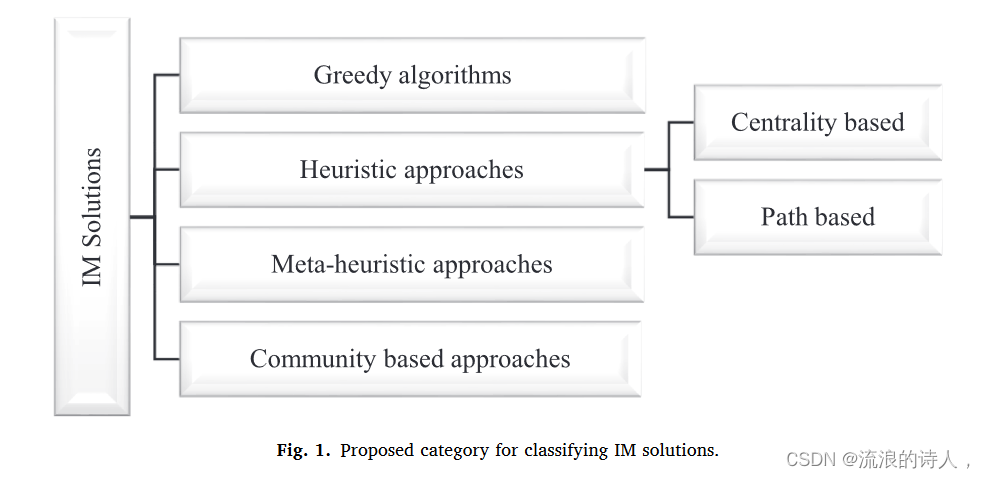
??肯佩等人。 (2003) 是第一个通过提出许多解决 IMP 的策略来解决该问题的人。他们在2003年猜想了贪心逼近算法，并证明了IC和LT模型下的IM问题是NP-hard问题，需要大量的计算。系统蒸发散以获得精确的解决方案。他们证明，在应用蒙特卡罗方法的情况下，多项式模拟使得可以很好地近似 σ(S)（给定种子集 S）。从那时起，人们提出了大量的策略来解决IMP，一般可以分为五类：（1）近似算法； (2) 启发式方法； (3) 元启发式方法； (4) 基于路径的方法； (5) 基于社区的方法。图 1 给出了所提出的分类法的图示，如下所述。

3.1.Greedy approaches

??肯佩等人。 (2003) 证明了 σ(?) 函数既是次模函数又是单调函数。因此，IM 问题可以通过具有可证明保证的简单贪心方法来近似。在实际应用中，贪心算法的解非常接近最优解，但该算法非常耗时。为了缓解传统贪心算法耗时的问题，Leskovec 等人。 (2007) 使用子模块性并提出了另一种名为 CELF 的贪婪算法。该算法在每次迭代中挑选出具有最大边际增益的节点。每次迭代中选定节点的边际增益必须大于之前的边际增益。该算法的主要优点是减少了评估影响力传播的调用次数。受 CELF 方法（Goyal、Lu 和 Lakshmanan，2011a）的启发，CELF++ 进一步改进了这一策略，它以同时的方式估计算法两个步骤的影响扩散，但运行时间非常长。海达里等人。 (2015) 提出了一种名为 SMG 的可扩展贪婪算法，该算法通过应用图结构来减少传播估计的数量。这种应用模拟的算法被称为简单贪婪算法，它产生接近最优的解决方案。此类算法的主要缺点是执行时间，即包括数百万个节点和数亿个边的网络的运行时间可能需要几个小时，这使得它们很慢并且无法在可接受的时间内找到有影响力的节点。

3.2.Heuristic algorithms

??研究人员还尝试通过启发式算法删除所需的模拟来降低时间复杂度，其中仅应用蒙特卡罗模拟来估计找到种子集后的最终值。寻找最大影响力传播的最佳种子节点的简单启发式方法是使用预定义的中心性指标。陈等人。 (2009)提出了单一折扣(SD)算法，其中假设节点的影响力根据节点的度中心性而增加。 SD 选择度数最高的节点，然后减少其直接邻居的值。

??作为类似的工作，Wang 和 Feng (2009) 提出了基于节点势的 TW 算法，Kundu 等人提出了基于节点势的 TW 算法。 (2011)提出了一种基于节点扩散度的算法。

? ?一组研究对网络中扩散路径的影响进行了建模。 （Kimura & Saito，2006）提供了一个独立的级联模型，其中影响扩散的概率是根据节点之间的最短和第二短路径计算的。戈亚尔等人。 (2011a,2011b)提出了Simpath算法，其中应用节点之间的路径来评估影响并通过顶点覆盖来优化候选节点的数量。唐等人。 (2014) 提出了两阶段影响最大化 (TIM)，以形成理论和实践之间的桥梁。 (Kim et al., 2013) 引入了一种可扩展且可并行的算法，名为 IPA，其中假设节点之间的路径是独立的。该算法仅计算路径的影响力分布，不关心影响力分布计算过程中网络的其他属性。金等人。 (2017)提出了RWP-IPA，采用随机游走方法来加速IPA。这种方法的缺点是，需要在预处理结束时以实验方式指定用于计算影响扩散的节点数量。

??与贪心算法相比，启发式算法不保证返回解与最优解的距离，但它们通常具有更好的运行时间和可扩展性。在启发式算法中，基于路径的算法实现了效率和效果之间的平衡。基于路径的算法的弱点是在某些网络上的解决方案较差，并且需要大量内存来存储路径。本文提出了一种新的基于路径的方法，并利用度中心性改进了其解决方案，并通过应用一些策略减少了内存需求。

3.3.Meta-heuristic algorithms

??一群研究人员使用元启发式算法来解决基于进化方法的 IM 问题。通过使用这种方法（Bucur & Iacca，2016），提供了一种使用遗传方法的新颖算法。他们表明，遗传方法可以在更好的运行时间内找到社交网络中有影响力的节点。根据结果??，该方法估计的影响范围在大多数情况下可以达到接近基本贪心算法的近似。江等人。 (2011) 提供了 IC 模型下的模拟退火方法，并采用多种启发式方法来加速 top-k 节点识别。崔等人。 (2018)给出了一种新颖的方法，即DDSE算法，它起源于差分进化算法。 DDSE算法根据(Jiang et al., 2011)提出的EDV度量计算期望IS，以解决基于度降序搜索策略的IM问题。 Kong 等人提出了局部影响力估计 (LIE)，度量来识别前 k 个节点，并提供离散粒子群优化 (DPSO) 算法，该算法可优化 LIE 适应度值。蔡等人。 （2015）提出了一种将遗传算法与强度贪婪算法相结合的新算法，并提出了遗传新贪婪（GNA）算法。一般来说，这些算法不会对影响力传播给出任何最坏情况的限制。而且，与贪婪的算法相比，它们没有理论上的保证来证明它们可以逃离局部最优。然而，实验结果表明，此类算法可以以良好的质量和合理的执行时间识别最有影响力的节点。

3.4.Community-based algorithms

??第四类 IM 算法的灵感来自于社区在信息传播中的关键作用。这些算法首先将网络划分为社区，然后将每个节点的影响力传播到其社区而不是整个网络。博佐尔吉等人。 （2016）提出了一种基于社区的 INCIM 方法，首先检测非重叠社区，然后根据其社区评估和排序每个节点的影响力传播，作为本地影响力传播，然后对社区的影响力进行评估和排序，如通过它们之间的边缘计算彼此之间的全球影响力分布。最后，通过比较各个社区的最佳节点，选出有影响力的节点。

? ??ch 社区。曹等人。 (2011)提出了一种名为OASNET的基于社区的算法，他们通过社区检测来评估每个节点的影响力，并将社区视为独立并应用CNN算法将初始社区划分为子社区。 Shang 等人提出了另一种基于社区的方法。 (2017)解决大规模网络中的 IM 问题。所开发的方法包含两个阶段：不同社区之间的种子扩展和社区内传播，在独立社区内传播影响力。

? ?一般来说，基于社区的算法比贪婪算法更快。此外，由于这些算法假设社区是隔离的，因此它们可以支持并行化。然而，当前类型方法的主要缺点是它们依赖于社区结构和社区检测算法。”

4.HIPA algorithm

??所提出的算法 HIPA 是一种有效的基于路径的方法，用于解决 IC 模型下的影响最大化问题。 HIPA的伪代码和框架分别用算法1表示和图2所示。如图 2 所示，HIPA 包括以下三个主要阶段：

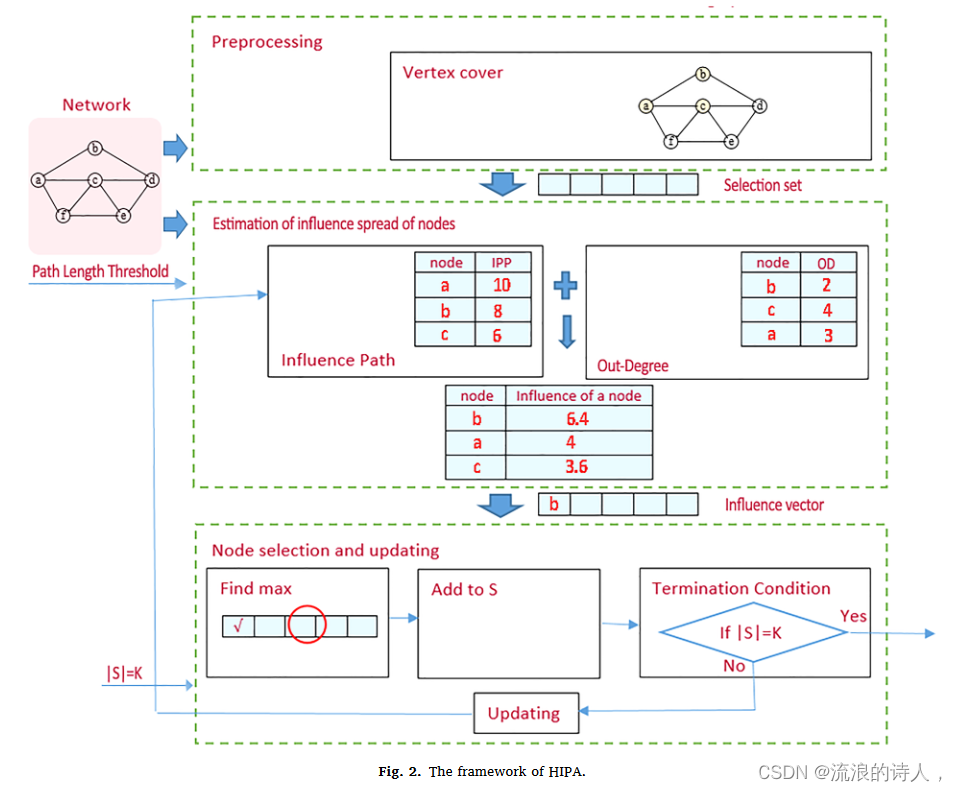
1 预处理：很明显，在计算影响力传播过程时，大规模社交网络的图涉及大量无效节点。删除全部或部分这些节点可以有效减少计算时间。 HIPA 执行预处理，包括查找一组节点覆盖，从而修剪原始图，然后将剩余节点作为选择集传输到下一步。

2 估计节点的影响力传播：HIPA结合了图的两个结构属性，两个节点之间的度和可用路径，用于计算网络中的影响力传播。因此，该算法除了提供节点影响扩散的良好近似之外，还降低了蒙特卡罗模拟的时间复杂度

3 选择节点和更新路径：在此过程中，在 k 次迭代中以渐进的方式进行第一次节点选择，其中在每次迭代中，选择最有影响力的节点并将其添加到有影响力的节点集（S）中，然后，基于IC模型更新所选节点的直接邻居和间接邻居、所选节点影响范围内的节点。

4.1.Phase 1: Preprocess

? ?社交网络在人们之间的效用不断增强，社交网络的规模急剧增长，因此需要对大量节点进行评估，寻找有影响力的节点。因此，应用预处理来从估计过程中消除一些节点将有助于减少计算开销。在预处理阶段，即HIPA中的第一阶段，对最终结果没有影响并导致更多速度减慢和更高内存利用率的节点被排除在计算过程之外。 HIPA 至使用顶点覆盖来实现这一目标。给定图的顶点覆盖，由顶点子集组成，其中每个图边都与该子集中的至少一个顶点相关。寻找最小顶点覆盖是图论中的优化问题。顶点覆盖问题表示为：给定一个图G(V,E)，其中V和E分别是顶点和边，顶点覆盖问题找到一组D?V，其中，?(u,v)∈E?u ε D ∨ v ε D 成立。

??尽管在图中找到最小顶点覆盖是一个 NP 完全问题，但可以找到有效的次优解决方案。当前为实现这一目标的研究使用算法 2 作为近似算法，该算法采用 O (|V|+|E|)。该方法确保顶点覆盖尺寸不会像最小顶点覆盖尺寸那么大（Cormen et al., 2009。

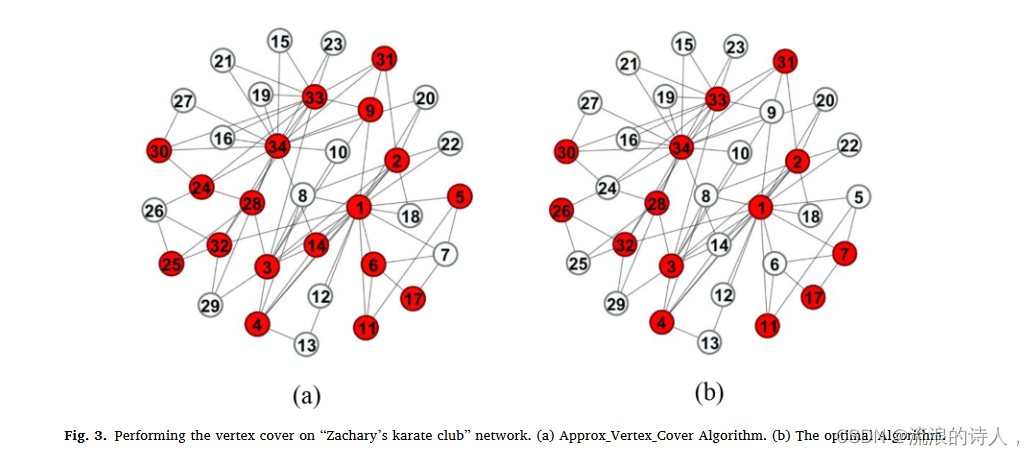
??在算法2中，顶点覆盖由VC表示，VC在算法开始时为空（第1行）。在第 2 行中，seté 被视为图边集 (E) 的副本。在一个迭代循环中（whileE^á∕=?），从é中选择一条边（u，v），将端点u和v添加到VC中，并从节点u和v中删除所有与节点u和v相连的边集合é。算法 2 返回集合 VC 作为输出选择集合。该算法应用于“Zachary’s karateclub”数据集（Zachary，1977），图 3.a，其中输出是 34 个节点中的 18 个节点，以红色表示。 “Zachary's karate Club”网络的最优顶点覆盖如图 3.b 所示。因此，在“Zachary's karateclub dataset”上运行此预处理会导致计算量减少近 50%，因为主要算法运行仅在一半节点上进行计算。

??

4.2.Phase 2: Estimation of influence spread of nodes

? ?这里，需要评估每个节点的影响力传播。为此，HIPA形成了选择集节点的向量，称为影响力传播向量，并应用“影响力传播路径”和“程度”的组合来设置其元素。

??寻找 HIPA 中的影响传播路径与（Kim et al., 2013）中描述的类似，其中需要搜索从图的任何源节点到其他节点的所有有效非循环路径，可以是通过深度优先搜索方法（DFS）完成。查找两个节点之间的所有可能路径非常耗时并且需要大量内存。为了克服这个缺点，可以忽略影响范围太小的路径。由于影响传播随着路径长度的增加而减少，因此 HIPA 应用“路径长度”阈值 (θ) 来消除传播概率低于阈值的路径。

??因此，仅研究不拒绝名为有效路径的阈值的路径并将其存储在存储器中。如果 v 和 u 节点之间的有效路径集合表示为 Pvalid u→v = {p1, p2, ?, pl}，则其影响力传播传播将是有效路径影响力传播的乘积，表示为 σ ?uP({v} ），并通过等式定义。 （2）：

其中 ipp(p) 是通过式（1）获得的通过路径 p 的影响传播概率。 （3）：

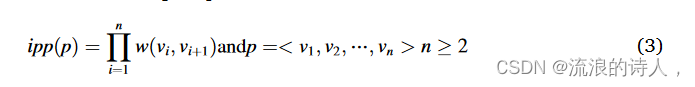
其中w(vi, vi+1)是vi和vi+1之间的边的权重；给定0≤ipp(p)≤1，为了减少小数乘法的计算误差，式(1) (2) 可以改写为等式： (4) 等价于 Pvalid v→u 中没有路径激活 u 的概率的补集。

估计节点通过路径的影响传播已经并正在被许多算法应用（Chen et al., 2010; Kim et al., 2013, 2017），但是它们没有区分不同的路径。 HIPA 假设到达目的节点的不同路径的价值是相关的，即目的节点的价值和影响力越大，其激活对总价值最大化的作用越显着。

影响。因此，通向该节点的任何路径都将更有价值，这表明该 HIPA 中每个节点 v 到节点 u,σ ?u H({v}) 的影响传播的估计是通过乘以“路径的影响传播概率”来估计的。节点 v 和 u 之间，” σ ?u P({v})，通过“网络中目标节点 u 的值” σ ?I({v}) ，等式：

HIPA利用强大的启发式度函数来获取每个节点的值，以简化相关性和加速计算过程。由于每个节点的影响力传播能力取决于其出度，因此出度较高的节点更有价值（Goyal，Lu，＆Lakshmanan，2011a）。另外，HIPA通过目的节点u的出度dout u 与网络中最高出度的比值，得到节点u在整个网络中的值，式(1)： （6）。

? 考虑图 4a 中的加权图，

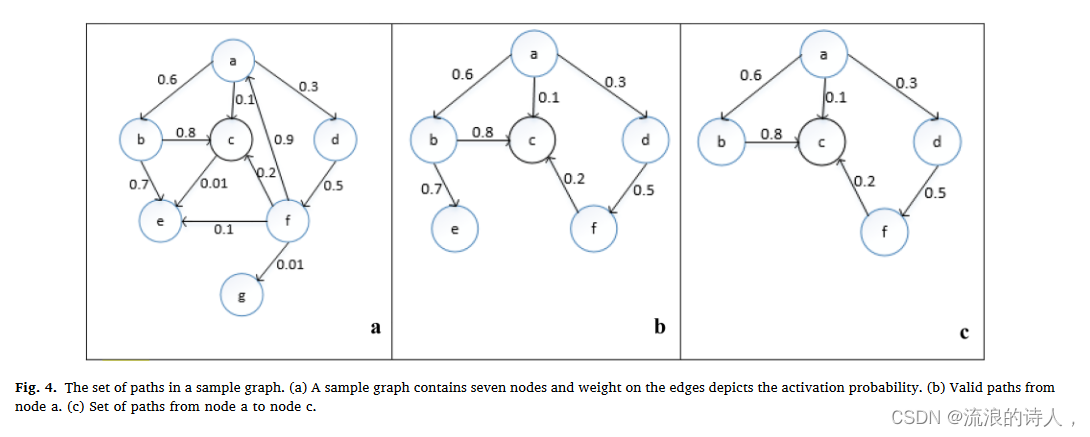其中包含七个节点，边上的权重表示源节点激活目标节点的概率。从源节点a开始的所有有效路径如图4b所示。如果θp = 0.02，为了评估节点a对节点c的影响，从源节点a到目的节点c的所有有效路径，图4c，并且给定t ∈ V max {dout t } = 4，计算节点a对c的影响值如下：

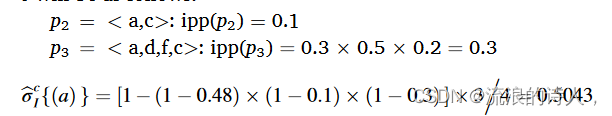
算法 3 中观察到了估计 HIPA 中节点影响力传播的伪代码。该算法的输入包括图 G、选择集 Vs 和路径长度阈值 θp。在算法的第 1 行中，影响扩散向量 (I-Vec) 被视为空。在 Vs 大小的迭代过程中，评估选择集 Vs 中每个节点 v 的影响范围（第 2-7 行），并将有序对 (v,σ?u H({v}) ) 添加到向量中I-Vec。每个节点v的影响力分布是将节点v与节点v影响区域内所有节点的影响力分布总和相加得到，Ov式： （7）。节点 v 的影响区域被称为节点集合，其中从 v 到它们至少有一条有效路径，通过式（1）表示。 （7）：

其中1是激活节点v的可能性，这也见于算法3的第3行。第4行根据路径长度阈值(θp)获取节点v的有效路径，其时间复杂度为O(|Ov|. ???Pvu ???）。 ???Pvu ???是节点v的有效路径的平均长度，Ov是节点v的影响区域。第5行中的循环通过将节点v对每个目标节点（如u）的影响扩散根据式（1）求和来计算节点v的影响扩散。 (7)，取|Ov|。最终，算法 3 返回影响力传播向量作为输出。算法3的总时间复杂度为O(|Vs|.|Ov|.???Pvu ???)。由于路径独立于起始节点，基于独立级联模型，算法 3 的第 2 行可以并行运行，从而将算法的复杂度降低到 O ( |Vs | c .|Ov|. ???Pvu ??? ) ，其中，c 是并行化的CPU 核心数。

4.3.Phase 3: Selecting nodes and updating path

??从算法1（HIPA算法的总体框架）中可以看出，k个有影响力的节点被表示为S，其中S的成员通过k次选择节点迭代以贪婪的方式找到。在每一步中，计算每个节点的影响力后，选择最有影响力的节点并将其添加到集合 S 中。选择节点 v 后，根据 IC 模型更新其影响范围内的节点，因为 1）经过的路径S集合在计算节点影响力扩散时必须无效，2）种子节点之间的路径必须被忽略。节点v路径的更新过程如图5所示，

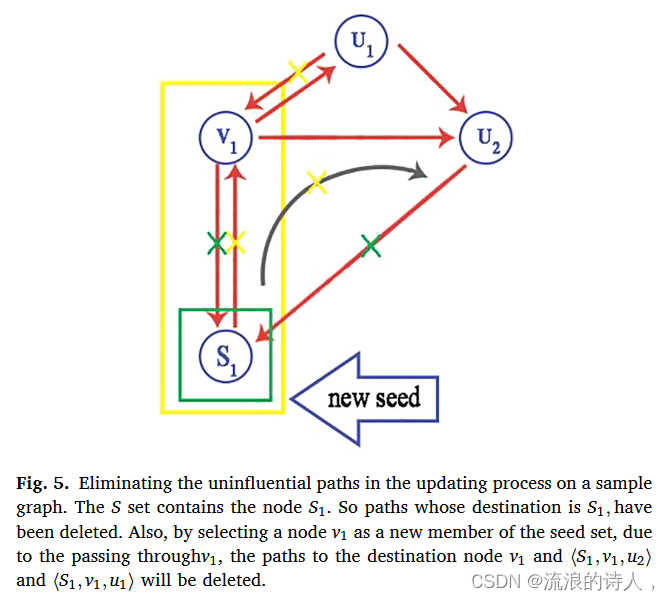
图 5. 消除样本图更新过程中无影响的路径。 S集合包含节点S1。因此，目的地为 S1 的路径已被删除。另外，通过选择节点 v1 作为种子集的新成员，由于经过 v1，到目的节点 v1 和 <S1, v1, u2> 和 <S1, v1, u1> 的路径将被删除。

??其中，种子影响区域中路径的消除是明显的。为了方便访问并避免在更新过程中重新加载路径，HIPA 对上一步收集的路径进行分类，并根据与影响力传播向量（I-Vec）类似的源节点进行保存。而且，它根据目的节点对来自每个源节点v的有效路径进行分类，使得轻松访问成为可能.

??在HIPA中保存路径的策略示例如图6所示，其中从vi touj有3条路径，标记为asp1、p2和p3是明显的。保存轨迹表如图 6 所示，以节点 vi 为源节点，根据表 PT(vi) 进行分组保存，目的节点为表中第 i 行。 PT表，图6。该表的第j行显示了isuj的目的节点的路径。

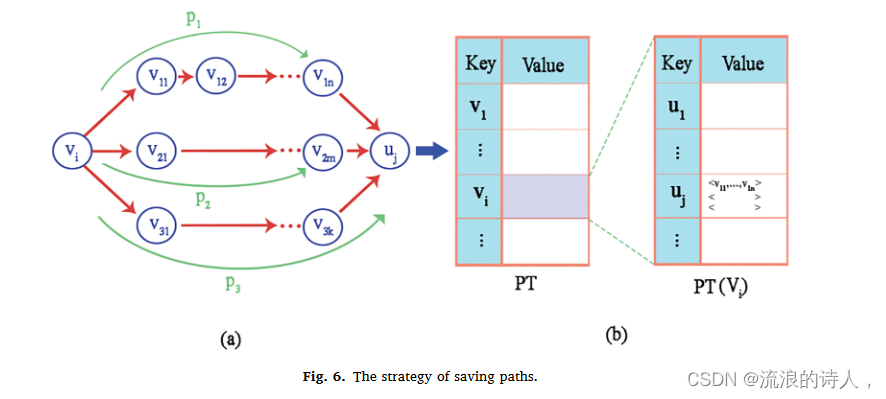
??更新过程的时间复杂度为O(|Ov|. ???Pvu ???)。 HIPA中保存路径的策略使得通过目的节点访问路径成为可能，从而可以并行地进行路径更新，并且该步骤的时间复杂度降低到O(|Ov|c. ???Pvu???）。

5.Experiments and discussions

??这里应用七个真实数据集来运行实验，以确定预处理方法的有效性，比较HIPA算法与其他算法的运行时间，以及比较不同算法的HIPA影响范围。

5.1.Experimental setup

表 2 列出了以下七个真实世界数据集的特征。

1.AstroPh 网络（Leskovec 等，2007）。 Arxiv ASTRO-PH（天体物理学）协作网络，其中描述了论文作者之间的科学合作。这些数据是由 Leskovec 等人于 2007 年收集并提交给天体物理学类别，时间跨度为 1993 年 1 月至 2003 年 4 月的十年。

2.P2p-Gnutella31 网络（Leskovec 等人，2007 年；Ripeanu 和 Foster，2002 年）。通过拍摄 2002 年 8 月的 Gnutella 对等文件共享网络的一系列快照，该网络由 62,586 个节点和 147,892 个边构成。节点和边分别代表主机和主机之间的连接。

3.Epinion 网络（Richardson 等，2003）。该网络借鉴自 Epinion 站点 (www.Epinion.com)，其中每个节点代表一个客户作为用户，每条边代表一个信任相关性。

4.Slashdot0811 社交网络（Leskovec 等人，2009）。 Slashdot 是一个流行的技术相关新闻网站，用户可以在其中将其他用户标记为朋友或敌人。该网络成立于2008年11月。

5.Slashdot0902 社交网络（Leskovec et al., 2009），成立于 2009 年 2 月。

6.斯坦福网络（Leskovec 等，2009）。该网络借用自斯坦福大学 (www.stanford.edu)。在这个网络图中，节点代表页面，边缘代表其中的超链接

7.巴黎圣母院网络。一个网络图，其中节点代表圣母大学 (www.nd.edu) 的页面，边代表其中的相关性。

将所提出的 HIPA 算法与以下算法进行比较：

Greedy：通过应用 10,000 次蒙特卡洛模拟来测量影响力传播。作为精确的近似结果，根据 IC 模型计算平均影响力分布（Leskovec 等人，

?SD:一种简单的度折扣启发式算法，当将节点添加到种子集中时，将其邻居的度减一

IPA:一种新的启发式算法，其中应用独立的影响路径来计算影响力传播（Kim 等人，2013）。

RWP-IPA:一种快速启发式算法，首先在主图上应用页面排名，然后通过 IPA 算法选择最有影响力的节点（Kim 等人，2017）。

TwoHop:受 IC ??约束的基于跳的算法（Tang et al., 2018）。

HIPA:该算法基于加权 IC 模型。根据（Kim et al., 2013），节点 v 激活节点 u 的概率通过 pvu = 1 din u 计算，其中，din u 是节点 u 的入度。

比较算法的特点如表 3 所示。

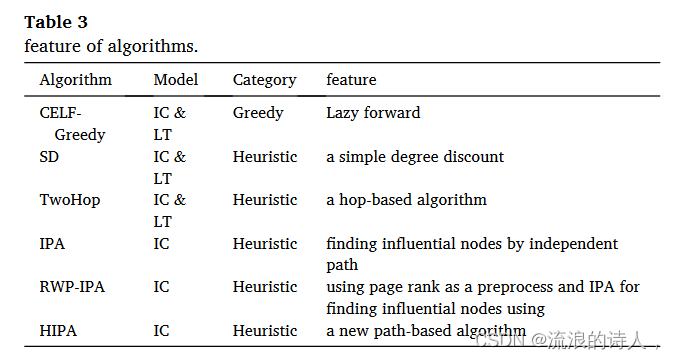
在本文中，应用了 20,000 次蒙特卡罗模拟，为了获得不同算法的影响力分布，考虑了平均影响力分布。该标准用于评估影响模拟中算法的质量和效率。所有实验均在windowsPC intel corei73.07 GHz、12 GB内存上运行。算法用java实现。

5.2.Experimental results

5.2.1. Parameter setting

HIPA算法与IPA类似，RWP-IPA由于通过路径施加影响传播，需要设置阈值来限制路径。路径长度阈值θp限制受通过路径的传播概率影响的有效路径的长度。随着 θp 缩小，正确路径的数量增加，因此，估计精度增加，处理时间显着增加。因此，确定θp值对算法效率有很大贡献。为了确定 θp 的适当体积，适应度函数 fk(θ) 在等式中定义。

其中 k 是初始种子集大小；Δtk,θ 是给定 k 的算法与等式 1 中定义的 θ 之间的执行时间差。 （9）。

其中 tk,θi 是具有一定 θi 的算法的执行时间，在某种意义上，θi 和 θi 1 是用于比较的连续阈值。变量Δσk,θ表示在tk,θi 1 和tk,θi 期间通过一定的k和θ获得的影响力分布的差异。 （10）。

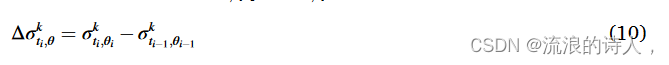
其中 10, σtk i,θi 是用 k 和 ti 得到的影响扩散率，从某种意义上说，ti 是执行阈值θi 时的执行时间，使得 θp 如下式所示： (11)如下。

不同数据集的 θp 估计值可能有所不同，因此，针对七个单独的数据集计算该参数，结果列于表 4 中。

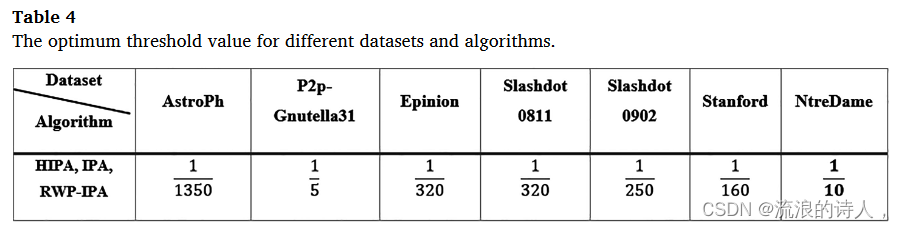
Slashdot0911 数据集每 θ 的 f50(θ) 值如图 7a 所示，其中水平轴代表 θ 值，在 0、1 范围内确定。根据该图，θ = 0.025 时 f50(θ) 的量最大。考虑到影响率随着时间的推移而增加的重要性，该点和在可忽略不计的执行时间内实现的下一个最大点 θ = 0.0125 被忽略，允许第三个最大点 θ = 1/250，这建立了更好的时间和影响传播速度之间的平衡，加以选择。

6.Conclusions and future works

? ? 在本研究中，提出了一种有效的启发式方法（HIPA）来解决社交网络中独立级联传播模型的影响力最大化问题。 HIPA作为一种启发式算法，旨在通过结合节点启发式函数之间的度和独立路径两个特征来估计影响传播。 HIPA估计功能使得该算法在其他一流算法中具有更好的影响力。该 HIPA 与五种算法进行了比较：IPA、RWP-IPA、SD、Twohop 和基本贪婪算法。 SD 和 Twohop 算法的处理时间与网络规模的增加直接相关，而 IPA 和 RWP-IPA 算法（如 HIPA）的处理时间取决于网络的密度。 TwoHop 揭示了 HIPA 在网络中获得最大影响力传播的优势。 HIPA 的另一个优点是应用预处理方法来减少执行时间。 HIPA的预处理阶段导致从影响扩散的计算过程中剪除无效节点并清除算法的输入。实验结果证实了该方法在提高影响力传播的同时减少了运行时间。 HIPA采用节点存储策略，提供每个节点路径的最优存储和高效搜索来计算节点的影响力传播。与 IPA 一样，由于传播路径的独立性，HIPA 可以并行化操作。它快速实用，同时增加了中央处理单元（CPU）核心的数量以在大规模网络上执行。

? ?因此，HIPA 在大规模和稀疏网络上表现更好，正如许多现实世界网络中所见。网络图（即斯坦福数据集）是一个很好的实用样本，广泛应用于商业广告等应用中。因此，对于未来的研究，建议：1）评估其他执行预处理和减少输入大小的方法，2）在其他信息传播模型上执行该方法并获得更完整的结果，3）提供一个调整路径的框架长度阈值，以便以自动和动态的方式确定有效路径。