正则化逻辑回归实战

一、题目

????????在正则化逻辑回归的练习中，我们将利用正则化的逻辑回归来预测来自制造工厂的微芯片是否通过了质量保证（QA）。在质量保证期间，每个微芯片都要经过各种测试，以确保其能够正常工作。假设您是该工厂的产品经理，并且您有两种不同测试中的一些微芯片的测试结果，从这两个测试中，您希望确定微芯片是应该被接受还是被拒绝。为了帮助您做出决定，您有一个关于微芯片的测试结果的数据集，利用该数据集您可以建立一个逻辑回归模型。

二、数据可视化

import pandas as pd
from matplotlib import pyplot as plt
import numpy as np
import scipy.optimize as opt

# 数据提取
path = "ex2data2.txt"
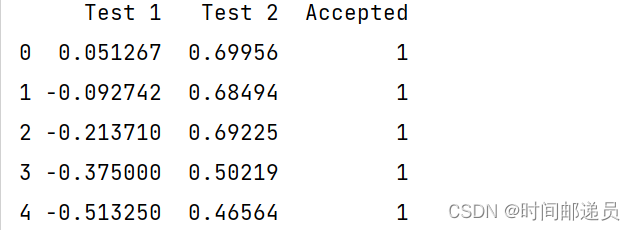
data2 = pd.read_csv(path, header=None, names=["Test 1", "Test 2", "Accepted"])
print(data2.head())

# 分别提取Accepted=1,Accepted=0的数据点
positive = data2[data2["Accepted"].isin([1])]
negative = data2[data2["Accepted"].isin([0])]

# 绘制图形：两种数据点：Accepted,Rejected
fix, ax = plt.subplots(figsize=(8, 6))
ax.scatter(positive["Test 1"], positive["Test 2"], s=20, color="blue", marker="o", label="Accepted")
ax.scatter(negative["Test 1"], negative["Test 2"], s=20, color="red", marker="x", label="Rejected")
ax.legend(loc=1)
ax.set_xlabel("Test 1 Score")
ax.set_ylabel("Test 2 Score")
plt.show()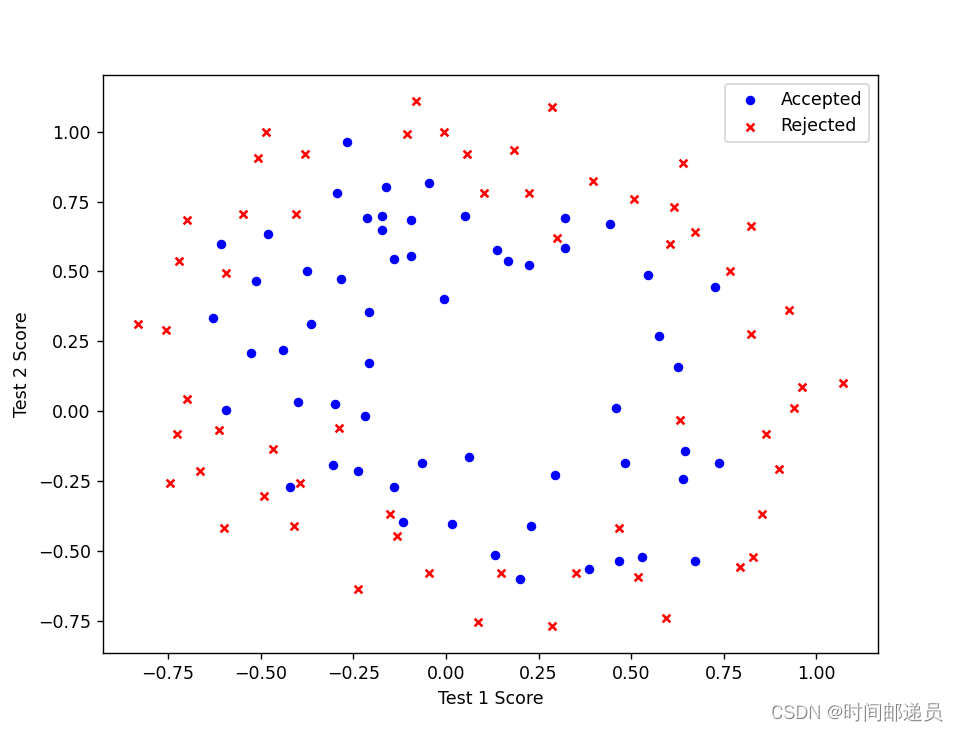

?

三、特征映射

????????如果样本多且逻辑回归问题很复杂，而原始特征只有x1,x2，则可以用多项式创建更多的特征，因为更多的特征进行逻辑回归时，得到的分割线可以是任意高阶函数的形状。为更好地匹配数据，我们从每个数据点中创建更多的特性，把这些特征映射到x1和x2的所有多项式项中，直到六次幂

# 创建多项式特征
# 设置最高次方为6
degree = 6
# 提取向量x1,x2
x1 = data2["Test 1"]
x2 = data2["Test 2"]
# 在data2中插入一列向量,全为1
data2.insert(3, "Ones", 1)
# 特征映射
for i in range(1, degree + 1):
    for j in range(0, i + 1):
        data2['F' + str(i) + str(j)] = np.power(x1, i - j) * np.power(x2, j)
# data2删除Test1,Test2列
data2.drop("Test 1", axis=1, inplace=True)  # 删除列需要axis=1;参数inplace 默认情况下为False，表示保持原来的数据不变，True 则表示在原来的数据上改变
data2.drop("Test 2", axis=1, inplace=True)
print(data2.head())

????????由于进行了特征映射，我们的2维特征向量已经被转换成了一个28维的特征向量。在这个高维特征向量上训练的逻辑回归分类器将有一个更复杂的决策边界，当在我们的二维图中绘制时将出现非线性函数图像。虽然特征映射允许我们构建一个更准确的分类器，但它也更容易受到过拟合的影响。在练习的下一部分中，我们将实现正则化逻辑回归来拟合数据，并自己看看正则化如何帮助解决过拟合问题。

四、代价函数

前面已经讲过正则化代价函数的表达式：

# 定义sigmoid函数：g(z)
def sigmoid(z):
    return 1 / (1 + np.exp(-z))


# 正则化代价函数
def costReg(Theta, X, Y, LearningRate):
    Theta = np.matrix(Theta)
    X = np.matrix(X)
    Y = np.matrix(Y)
    first = np.multiply(-Y, np.log(sigmoid(X @ Theta.T)))
    second = np.multiply(1 - Y, np.log(1 - sigmoid(X @ Theta.T)))
    # 正则项计算：
    reg = (LearningRate / (2 * len(X))) * np.sum(np.power(Theta[:, 1:Theta.shape[1]], 2))
    return np.sum(first - second) / len(X) + reg

五、梯度下降

????????如果我们要使用梯度下降法令这个代价函数最小化，因为我们未对进行正则化，所以梯度下降算法将分两种情形：

对上面的算法中 j=1,2,...,n 时的更新式子进行调整可得：

可以看出，正则化线性回归的梯度下降算法的变化在于，每次都在原有算法更新规则的基础上令值减少了一个额外的值。

# 梯度下降
def gradientReg(Theta, X, Y, LearningRate):
    Theta = np.matrix(Theta)
    X = np.matrix(X)
    Y = np.matrix(Y)
    Theta_cnt = Theta.shape[1]
    grad = np.zeros(Theta.shape[1])
    error = sigmoid(X * Theta.T) - Y
    for i in range(Theta_cnt):
        tmp = np.multiply(error, X[:, i])
        grad[i] = np.sum(tmp) / len(X)
    reg = (LearningRate / len(X)) * Theta
    reg[0] = 0  # θ0不考虑正则化，不惩罚第0项
    return grad + reg

计算最合适的θ：

cols = data2.shape[1]
# data2的列：Accepted x0 x1...
Y2 = data2.iloc[:, 0:1]
X2 = data2.iloc[:, 1:cols]
X2 = np.array(X2.values)
Y2 = np.array(Y2.values)
Theta2 = np.zeros(X2.shape[1])
LearningRate = 1
costReg(Theta2, X2, Y2, LearningRate)
gradientReg(Theta2, X2, Y2, LearningRate)
result2 = opt.fmin_tnc(func=costReg, x0=Theta2, fprime=gradientReg, args=(X2, Y2, LearningRate))
# result2[0]就是学习得到的θ
Theta_min = result2[0]

六、训练模型

def predict(Theta, X):
    p = sigmoid(X @ Theta.T)
    return [1 if x >= 0.5 else 0 for x in p]


predictions = predict(Theta_min, X2)
correct = [1 if a == b else 0 for (a, b) in zip(predictions, Y2)]
accuracy = float((sum(correct) / len(correct)) * 100)
print("accuracy = {:.2f}%".format(accuracy))


def hfun2(theta, x1, x2, degree):
    temp = theta[0][0]
    place = 0
    for i in range(1, degree + 1):
        for j in range(0, i + 1):
            temp += np.power(x1, i - j) * np.power(x2, j) * theta[0][place + 1]
            place += 1
    return temp


def find_decision_boundary(theta, degree):
    t1 = np.linspace(-1, 1.5, 1000)
    t2 = np.linspace(-1, 1.5, 1000)
    cord = [(x, y) for x in t1 for y in t2]
    x_cord, y_cord = zip(*cord)
    h_val = pd.DataFrame({'x1': x_cord, 'x2': y_cord})
    h_val['hval'] = hfun2(theta, h_val['x1'], h_val['x2'], degree)
    decision = h_val[np.abs(h_val['hval']) < 2 * 10 ** -3]
    return decision.x1, decision.x2


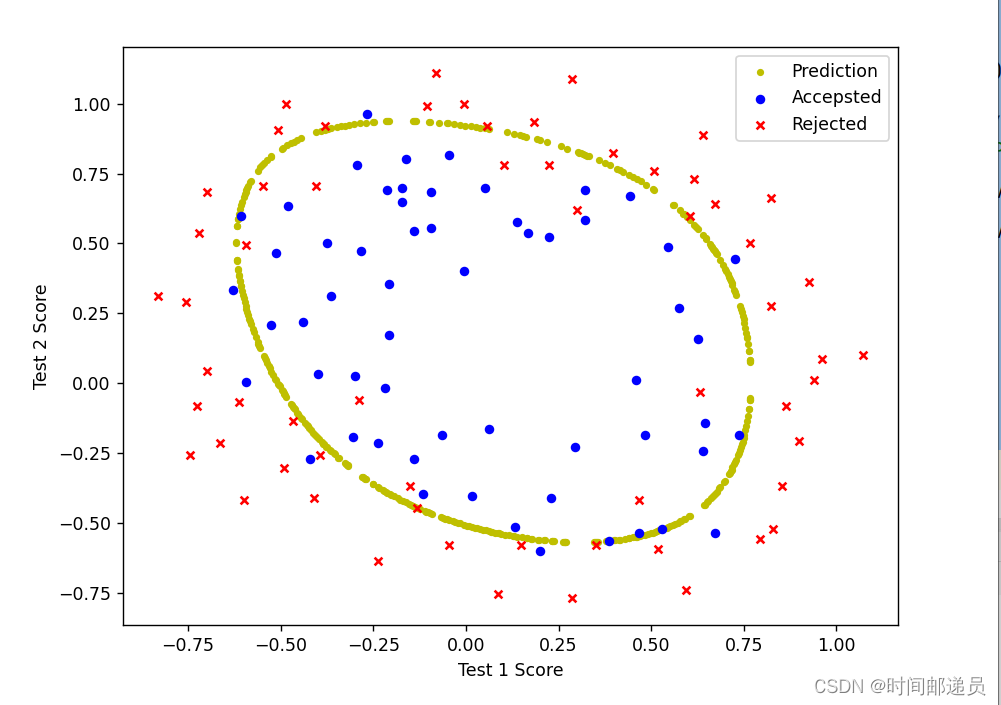
fix, ax = plt.subplots(figsize=(8, 6))
x, y = find_decision_boundary(result2, 6)
ax.scatter(x, y, c='y', s=10, label='Prediction')
ax.scatter(positive["Test 1"], positive["Test 2"], s=20, color="blue", marker="o", label="Accepsted")
ax.scatter(negative["Test 1"], negative["Test 2"], s=20, color="red", marker="x", label="Rejected")
ax.set_xlabel("Test 1 Score")
ax.set_ylabel("Test 2 Score")
ax.legend(loc=1)

plt.show()

?