力扣刷题记录--图相关题目

图的遍历方式主要是深度优先搜索（DFS）和广度优先搜索（BFS），两者大概的区别：

• dfs是可一个方向去搜，不到黄河不回头，直到遇到绝境了，搜不下去了，再换方向（换方向的过程就涉及到了回溯）。
• bfs是先把本节点所连接的所有节点遍历一遍，走到下一个节点的时候，再把连接节点的所有节点遍历一遍，搜索方向更像是广度，四面八方的搜索过程。

DFS:
dfs是离不开回溯的，因为它怼着一个方向深搜，当一个方向的搜索满足不了的时候，就需要回溯，回到前面的点换一个方向搜索。递归和回溯是相辅相成的，回溯法的代码框架：

void backtracking(参数) {
    if (终止条件) {
        存放结果;
        return;
    }
    for (选择：本层集合中元素（树中节点孩子的数量就是集合的大小）) {
        处理节点;
        backtracking(路径，选择列表); // 递归
        回溯，撤销处理结果
    }
}

dfs的代码框架：

void dfs(参数) {
    if (终止条件) {
        存放结果;
        return;
    }

    for (选择：本节点所连接的其他节点) {
        处理节点;
        dfs(图，选择的节点); // 递归
        回溯，撤销处理结果
    }
}

可以看出二者差别不大。

对于dfs同样是走着递归3步（来自代码随想录）：

1. 确认递归函数，参数：

通常我们递归的时候，我们递归搜索需要了解哪些参数，其实也可以在写递归函数的时候，发现需要什么参数，再去补充就可以。

一般情况，深搜需要 二维数组数组结构保存所有路径，需要一维数组保存单一路径，这种保存结果的数组，我们可以定义一个全局变量，避免让我们的函数参数过多:

List<List<Integer>> result; // 保存符合条件的所有路径
List<Integer> path; // 起点到终点的路径
void dfs (图，目前搜索的节点)  

2. 确认终止条件

终止添加不仅是结束本层递归，同时也是我们收获结果的时候。

另外，其实很多dfs写法，没有写终止条件，其实终止条件写在了， 下面dfs递归的逻辑里了，也就是不符合条件，直接不会向下递归。

if (终止条件) {
    存放结果;
    return;
}

3. 处理目前搜索节点出发的路径

一般这里就是一个for循环的操作，去遍历 目前搜索节点 所能到的所有节点。

for (选择：本节点所连接的其他节点) {
    处理节点;
    dfs(图，选择的节点); // 递归
    回溯，撤销处理结果
}

---

BFS:

广搜适合于解决两个点之间的最短路径问题。

因为广搜是从起点出发，以起始点为中心一圈一圈进行搜索，一旦遇到终点，记录之前走过的节点就是一条最短路。

借用代码随想录的例子：
给出一个start起始位置，BFS就是从四个方向走出第一步。如果加上一个end终止位置，那么使用BFS的搜索过程如图所示：

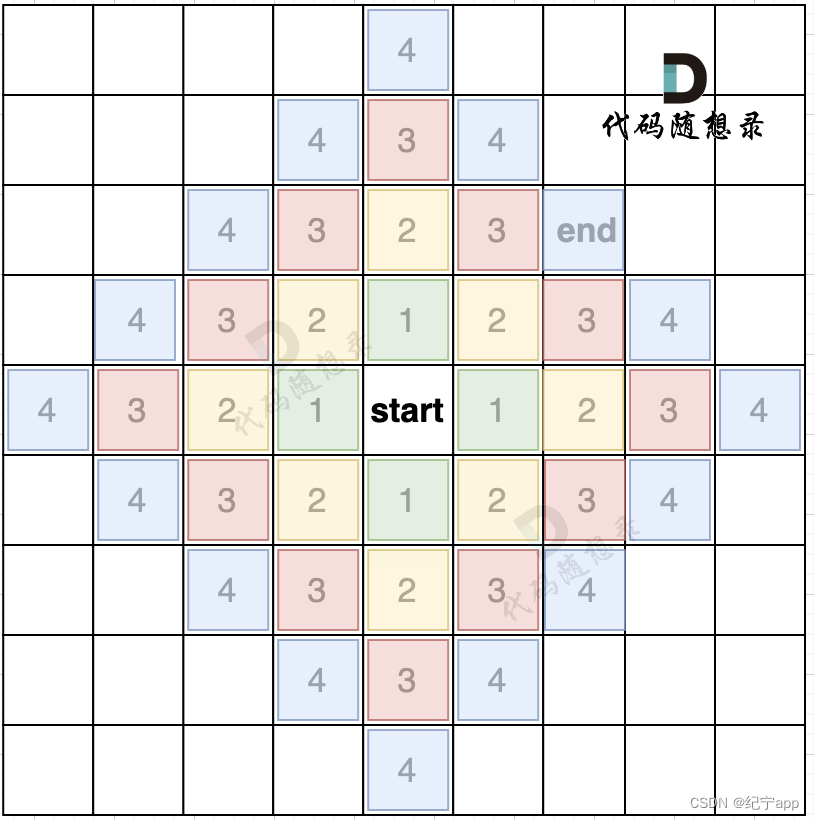
从图中可以看出，从start起点开始，是一圈一圈，向外搜索，方格编号1为第一步遍历的节点，方格编号2为第二步遍历的节点，第四步的时候我们找到终止点end。因为BFS一圈一圈的遍历方式，所以一旦遇到终止点，那么一定是一条最短路径。

而且地图还可以有障碍，如图所示：

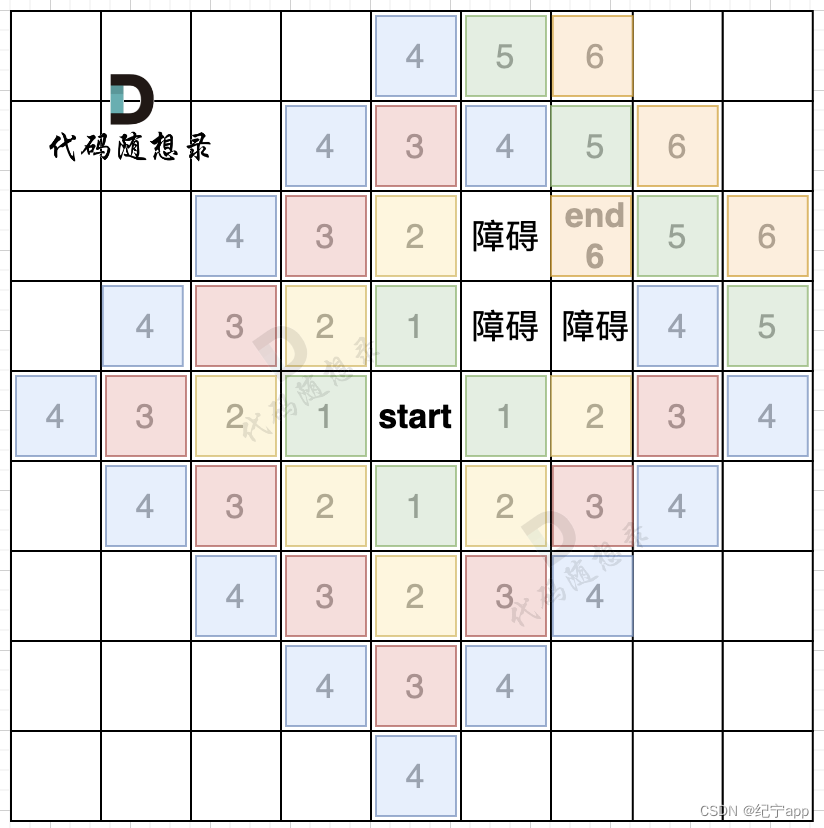
从图中可以看出，如果添加了障碍，我们是第六步才能走到end终点，所以只要BFS只要搜到终点一定是一条最短路径。

至于用什么样的数据结构，其实只要可以保存我们要遍历过的元素就可以，用队列，还是用栈，甚至用数组，都是可以的。用队列的话，就是保证每一圈都是一个方向去转，例如统一顺时针或者逆时针。

因为队列是先进先出，加入元素和弹出元素的顺序是没有改变的。

如果用栈的话，就是第一圈顺时针遍历，第二圈逆时针遍历，第三圈有顺时针遍历。

因为栈是先进后出，加入元素和弹出元素的顺序改变了。

而广搜不需要注意转圈搜索的顺序，只要能搜到就行了，但大家都习惯用队列了，所以大部分还是使用队列来存储遍历过的元素。

以下是代码随想录的c++版模板，针对四方格地图：

int dir[4][2] = {0, 1, 1, 0, -1, 0, 0, -1}; // 表示四个方向
// grid 是地图，也就是一个二维数组
// visited标记访问过的节点，不要重复访问
// x,y 表示开始搜索节点的下标
void bfs(vector<vector<char>>& grid, vector<vector<bool>>& visited, int x, int y) {
    queue<pair<int, int>> que; // 定义队列
    que.push({x, y}); // 起始节点加入队列
    visited[x][y] = true; // 只要加入队列，立刻标记为访问过的节点
    while(!que.empty()) { // 开始遍历队列里的元素
        pair<int ,int> cur = que.front(); que.pop(); // 从队列取元素
        int curx = cur.first;
        int cury = cur.second; // 当前节点坐标
        for (int i = 0; i < 4; i++) { // 开始想当前节点的四个方向左右上下去遍历
            int nextx = curx + dir[i][0];
            int nexty = cury + dir[i][1]; // 获取周边四个方向的坐标
            if (nextx < 0 || nextx >= grid.size() || nexty < 0 || nexty >= grid[0].size()) continue;  // 坐标越界了，直接跳过
            if (!visited[nextx][nexty]) { // 如果节点没被访问过
                que.push({nextx, nexty});  // 队列添加该节点为下一轮要遍历的节点
                visited[nextx][nexty] = true; // 只要加入队列立刻标记，避免重复访问
            }
        }
    }

}

---

LeetCode 797. 所有可能的路径

添加链接描述

2023.12.26 一刷

思路：

题目要求找出从0到n-1的所有路径，其实graph.length=n，n-1就是graph的下标；
graph[i]就是节点i可以到达的所有节点的列表；

可以采用图的深度优先搜索：
1.确认递归函数，参数
为了深度优先遍历，就需要把图作为参数；此外还需要知道当前遍历到了哪个节点，所以需要把节点也作为参数进行传递；

public void dfs(int[][] graph,int node)

2.确认终止条件
题目要求收集从0到n-1的路径，因此只要传进来参数节点是n-1（即graph.length-1）就视为路径完整，就将记录的路径收集进入res；

if(node == graph.length-1){
    res.add(new ArrayList<>(path));
    return;
}

3.处理目前搜索节点出发的路径
遍历到当前节点node后，需要知道节点node与谁相连，即graph[node][i]，用i从0到graph[node].length-1遍历所有node可以到达的节点，依次加入path并进行邻接节点的dfs，然后进行回溯，将路径中的当前节点去除；：

for(int i=0;i<graph[node].length;i++){
    // 记录邻接的节点
    int nextNode = graph[node][i];
    path.add(nextNode);
    dfs(graph,nextNode);
    path.remove(path.size()-1);
}

LeetCode 200. 岛屿数量

原题链接

一、深搜：

核心思想：
为了避免在递归过程重复计算之前已经遍历过的“陆地”，在dfs过程中需要将搜索过的“1”，置为“0”；
需要遍历grid的所有网格，一旦碰到为“1”的陆地，计数器就+1，然后进行dfs，将所有与之相连的“1”全部置为“0”。由于在深搜中会将邻接的“1”都置为“0”，因此不用担心重复计算岛屿的数量。

深搜代码如下：

//  解法1：深搜
class Solution {
    public int numIslands(char[][] grid) {
        int count=0;
        for(int i=0;i<grid.length;i++){
            for(int j=0;j<grid[0].length;j++){
                if(grid[i][j] == '1'){
                    count++;
                    dfs(grid,i,j);
                }
            }
        }
        return count;
    }
    public void dfs(char[][] grid,int i,int j){
        // 当超出网格界限或遍历到“0”，就可以返回了
        if(i<0||i>=grid.length||j<0||j>=grid[0].length||grid[i][j]=='0')return;
        grid[i][j]='0';
        dfs(grid,i-1,j);
        dfs(grid,i+1,j);
        dfs(grid,i,j-1);
        dfs(grid,i,j+1);

    }
}

二、广搜：
由于广搜需要搭配used数组标记已经访问过的陆地，因此遍历过程中不必像深搜一样将“1”的陆地置为“0”，只需对应网格标记为访问过即可；

遍历所有网格过程时，只有当前网格未访问过，且网格为“1”（陆地），才将岛屿数量+1，并进行bfs；

在bfs中，需要先将入队的网格标记为访问过，然后沿4个方向进行bfs，只有当要访问的网格未被访问，且为“1”，就将其入队（防止重复访问网格），并且立即将入队网格标记为访问过；

广搜代码如下：

//  解法2：广搜
class Solution {
    boolean[][] used;// 标记访问过的网格
    // 作为原始坐标方向偏移，与原坐标相加，依次是上下左右
    int[][] dir = {{-1,0},{1,0},{0,-1},{0,1}};
    public int numIslands(char[][] grid) {
        int count=0;
        used = new boolean[grid.length][grid[0].length];
        for(int i=0;i<grid.length;i++){
            for(int j=0;j<grid[0].length;j++){
                // 只有当未访问过且为1的陆地才可以+1
                if(!used[i][j] && grid[i][j] == '1'){
                    count++;
                    bfs(grid,i,j);
                }
            }
        }
        return count;
    }
    public void bfs(char[][] grid,int i,int j){
        Queue<int[]> que = new ArrayDeque<>();// 队列，用于暂存访问节点
        que.offer(new int[]{i,j});// 将当前网格入队
        used[i][j] = true;//只要一入队就必须标记为访问过

        while(!que.isEmpty()){
            // 队头先出队，找出与之邻接的符合要求的网格入队
            int[] cur = que.poll();
            int curI = cur[0];
            int curJ = cur[1];
            // 依次遍历上下左右四个方向的网格
            for(int d=0;d<4;d++){
                int nextI = curI+dir[d][0];
                int nextJ = curJ+dir[d][1];
                // 当超出网格界限，就可以继续下一个方向了
                if(nextI<0||nextI>=grid.length||nextJ<0||nextJ>=grid[0].length)continue;
                // 只有当下一个网格未访问过，且为‘1’，才加入队列
                if(!used[nextI][nextJ] && grid[nextI][nextJ]=='1'){
                    que.offer(new int[]{nextI,nextJ});
                    used[nextI][nextJ]=true;// 记得一加入队列就标记访问过
                }
            } 
        }
        
    }
}