数模学习day04-TOPSIS法

TOPSIS法的全称可以翻译为逼近理想解排序法，国内常常称为优劣解距离法

此方法是一种常用的综合评价方法，其能充分利用原始数据的信息，其结果能精确的反映各评价方案之间的差距。

1.层次分析法的局限性

其实这个在层次分析法的文章中已经提到过了，但是这里为了更加清晰的对比出来还是可以再提一嘴。

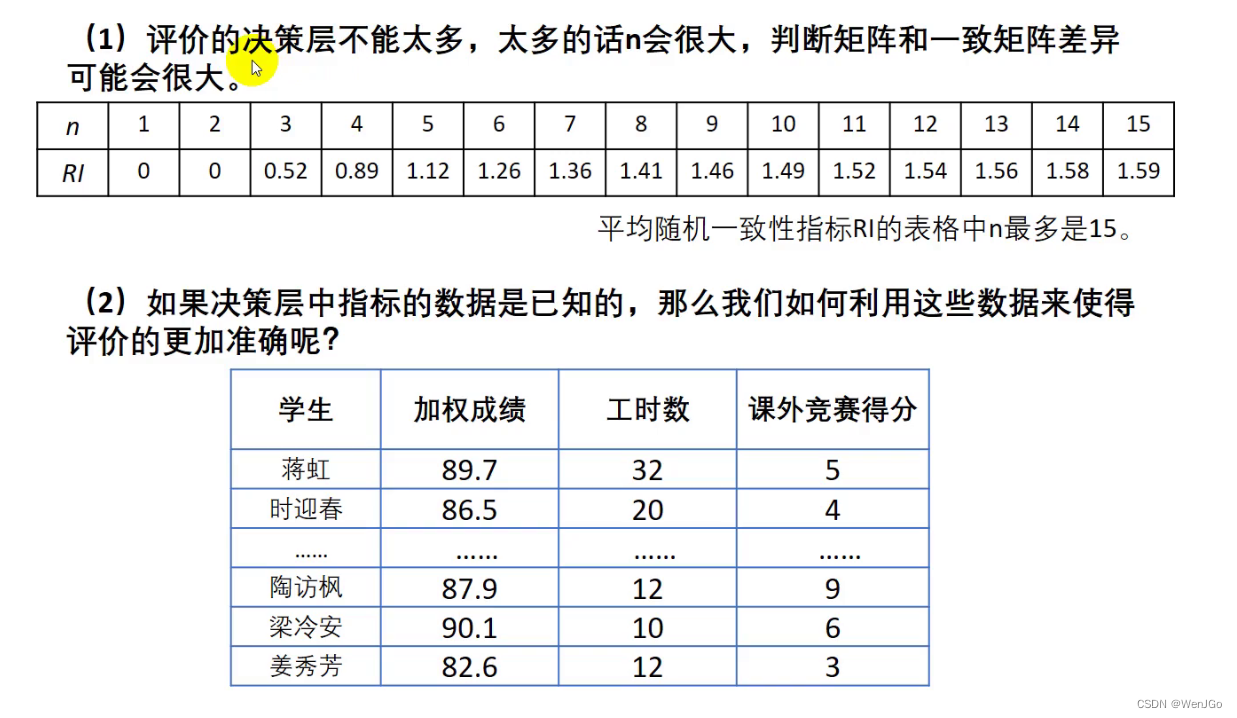
第一个大家都知道，但是如果是第二个的话，大家也知道层次分析法是让“专家”来填，是一个主观的行为是吧，如果是给出了具体的数据的话，就不需要使用层次分析法了。

---

2.例子引入

（1）基础问题

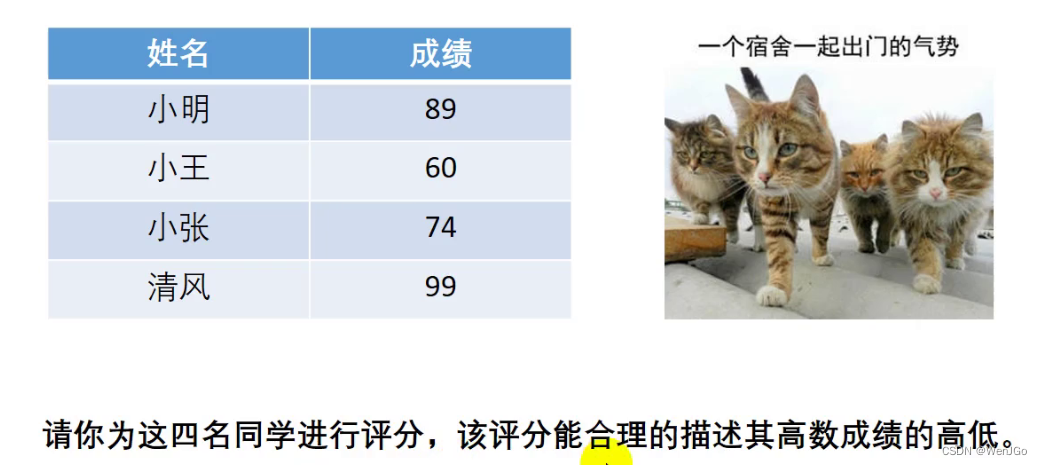
如何评分呢，将排名的分反过来即可

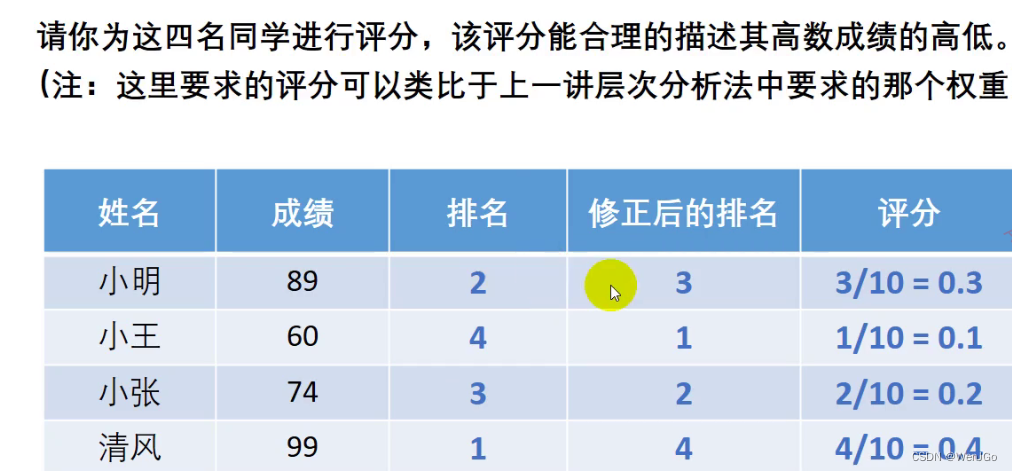
但是这样的话有一个BUG，只要排名不变，分数随意修改都可以，这是一个问题

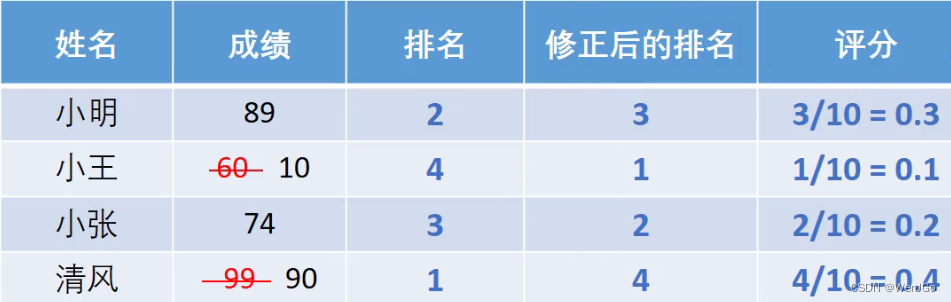
?那么就有一个全新的思路

可以将他们的分数纳入评分计算，这里采用归一化评分

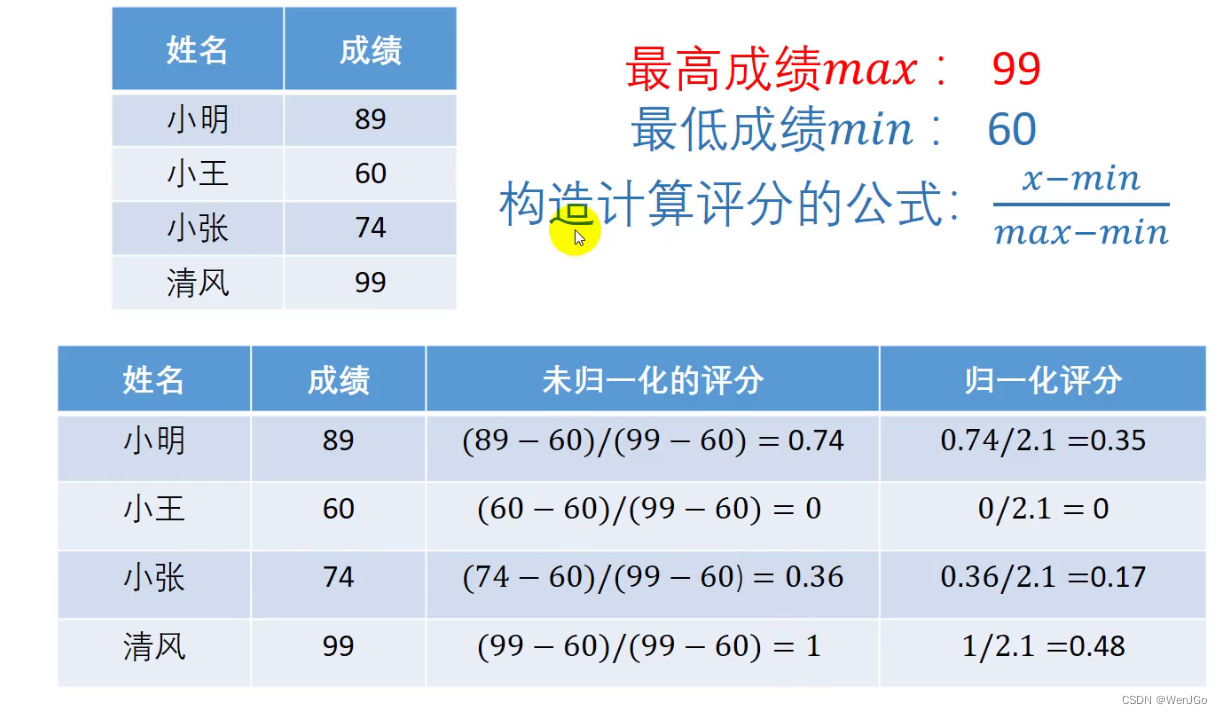
但是这里就会提出一个问题了，为什么这里是采用的卷面最高分和最低分，为什么不用100分呢？

这样就会使相关性更强啊。

主要有三点的考虑：

（1）比较的对象一般要远大于两个（例如比较一个小组的成绩）

（2）比较的指标一般也不知有一个（例如，绩点，综测，竞赛得分）

（3）有很多的指标并不存在理论上的最大值和最小值（例如GDP增速）

构造计算评分的公式：?

---

（2）拓展问题

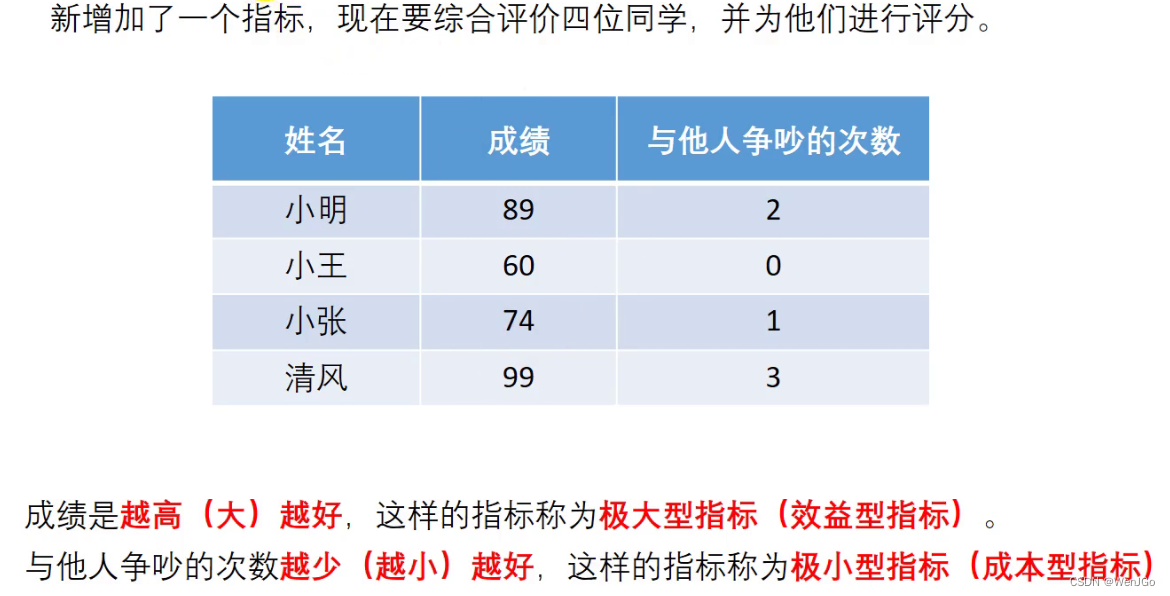
这是两个数据期待相反的指标，因此可以将所有的指标都转化为极大型称为指标正向化（最常用）

如果用到了这个方法，上面这句话写到论文中

极小型指标转换为及大型指标的公式?

?max - x

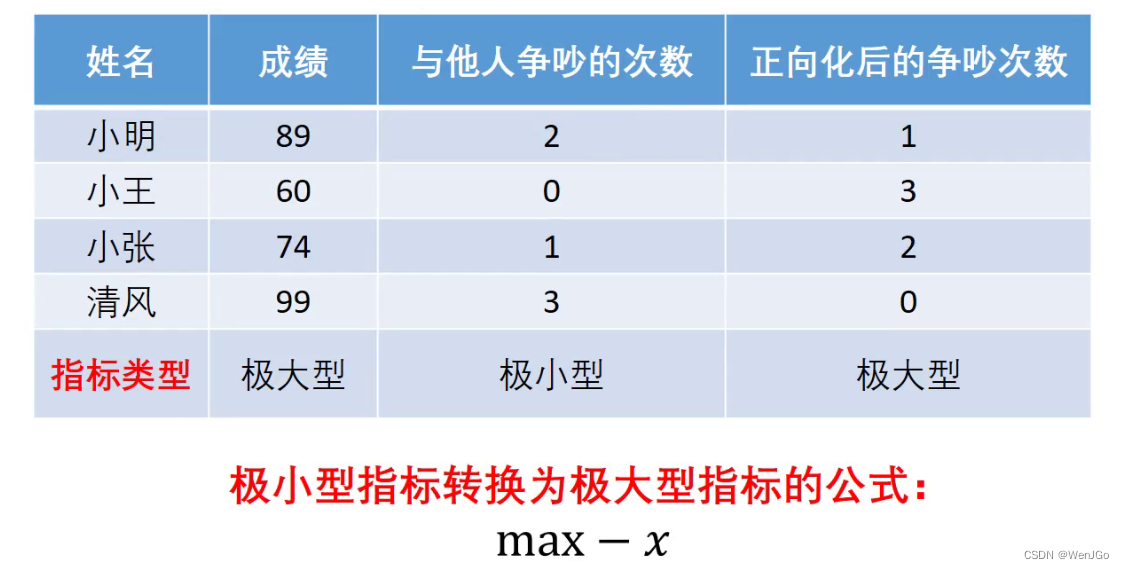
现在有一个新的问题了，这里虽然两个都已经是极大型了，但是如果直接相加起来除，还是有问题。什么问题，比如我又100万，你有一块钱，我是不是可以认为你没有钱。这是一个夸张的例子，也就是说，这里的成绩和正向化后的争吵次数，差值太大了，也就是量纲不同，因此我们需要对经过正向化的矩阵进行标准化处理

---

那么如何进行标准化处理呢：

标准化的计算公式

---

计算得分

?类比只有一个指标计算得分

回到题目计算得分：

---

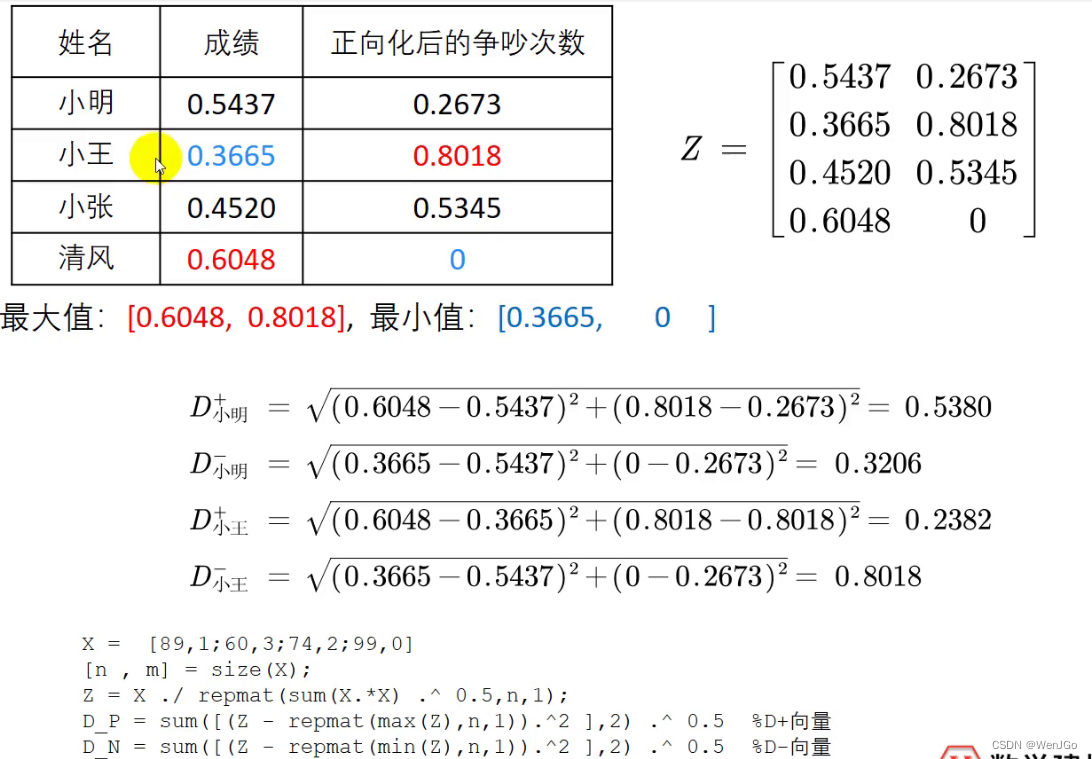
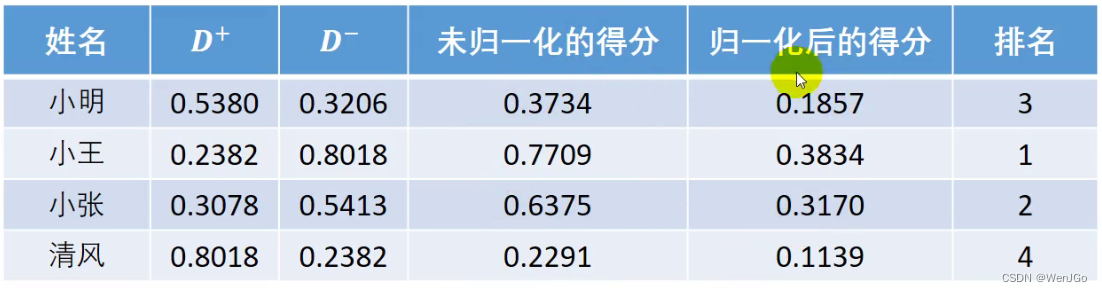
3.TOPSIS正式登场

---

（1）四种指标概览

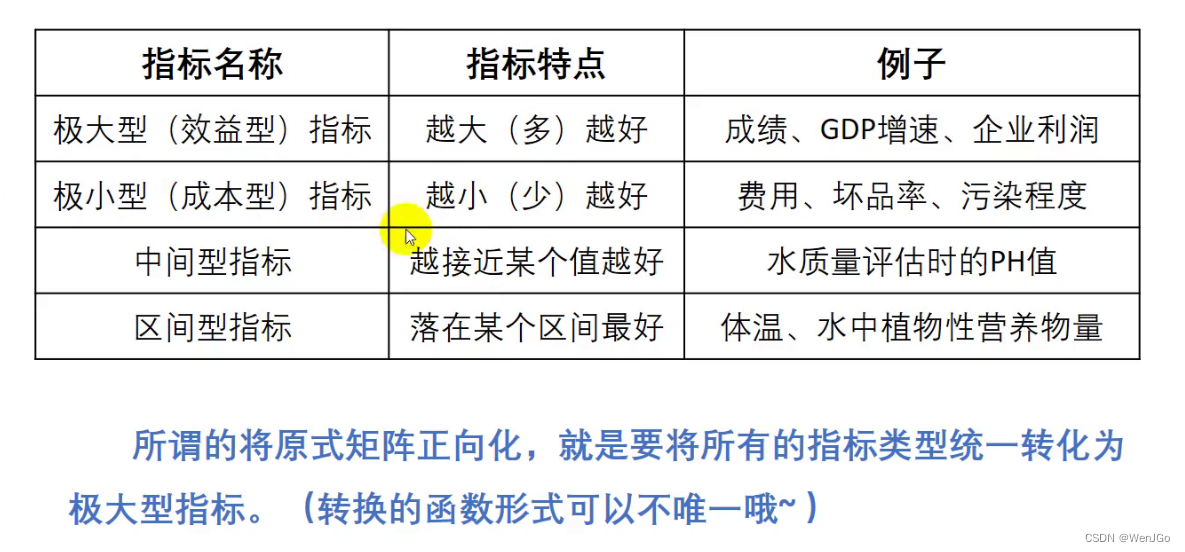
（2）TOPSIS第一步：将原始矩阵正向化

极小型==>极大型

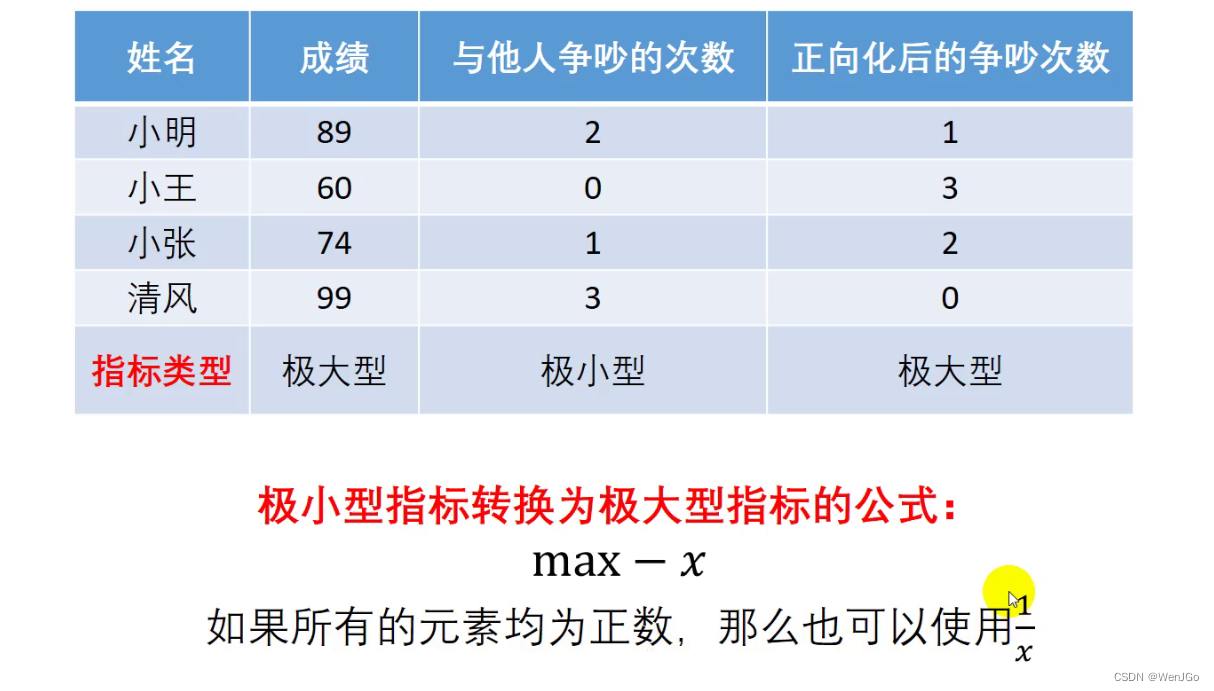
还是推荐直接使用第一种，因为没有限定条件

---

中间型==>极大型

---

区间型==>极大型

---

（2）TOPSIS第二步：正向化矩阵标准化

目的：为了消除不同指标量纲的影响

---

（3）TOPSIS第三步：计算得分并归一化

?

---

4.摩拳擦掌练习练习

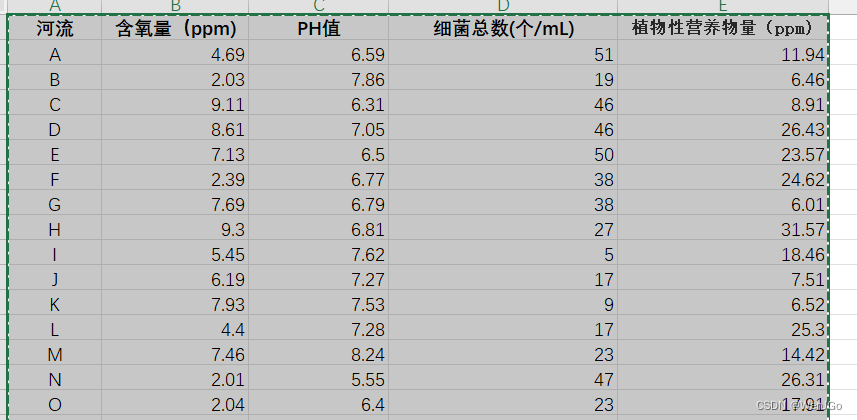
1.题目

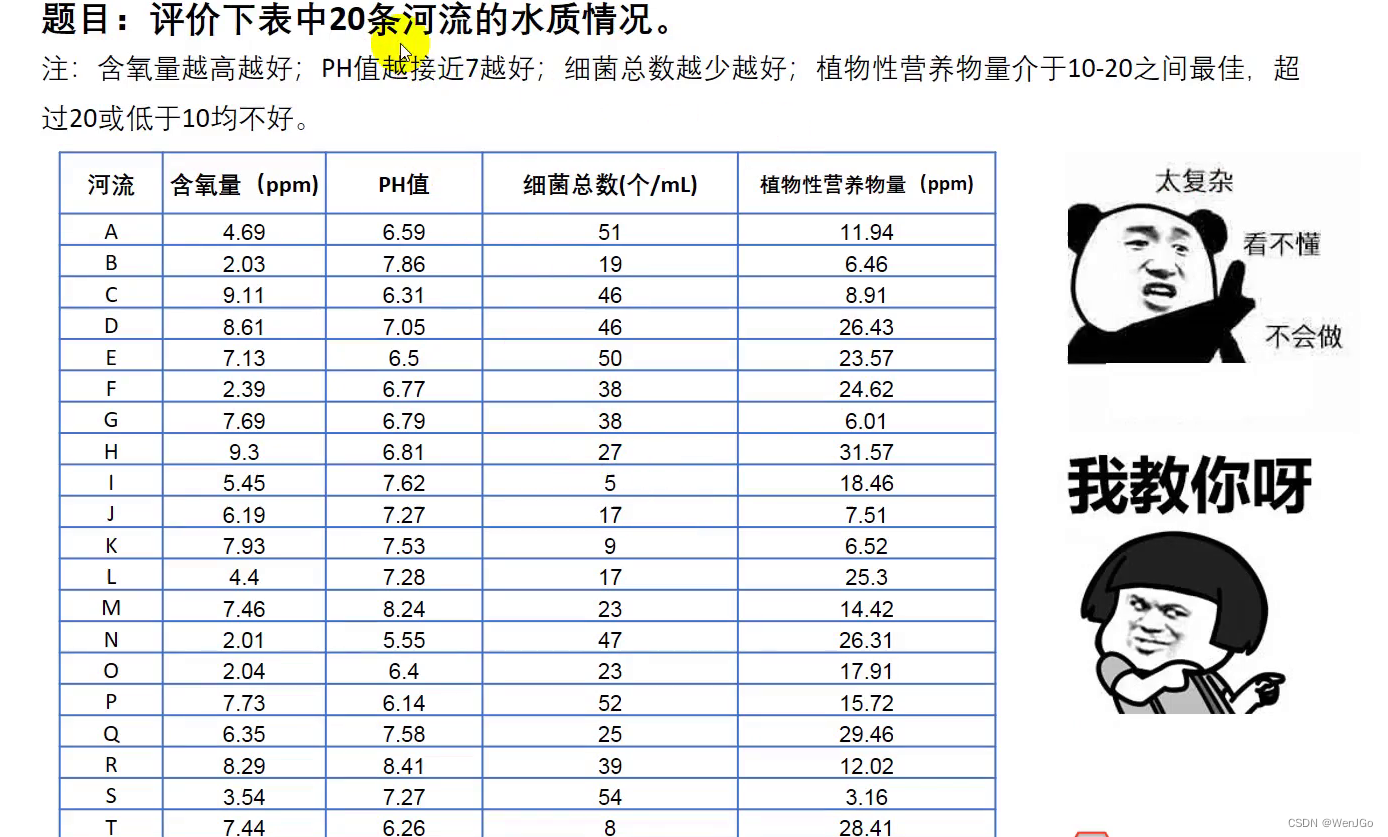
刚好每一个指标都有了

含氧量：极大型

PH值：中间型

细菌总个数：极小型

植物性营养物量：区间型

所以后面的几种都要转换为极大型

---

2.导入数据

新建一个原始数据

到Excel表格中粘贴

双击X打开

将表格中的数据粘贴进去

右键，点击粘贴Excel表格的数据，或者快捷键 Ctrl+Shift+V

另存为.mat文件

右键X，另存为当前的工作目录

加载文件load

---

3.topsis主文件

%%  第一步：把数据复制到工作区，并将这个矩阵命名为X
% （1）在工作区右键，点击新建（Ctrl+N)，输入变量名称为X
% （2）在Excel中复制数据，再回到Matlab中右键，点击粘贴Excel数据（Ctrl+Shift+V）
% （3）关掉这个窗口，点击X变量，右键另存为，保存为mat文件（下次就不用复制粘贴了，只需使用load命令即可加载数据）
% （4）注意，代码和数据要放在同一个目录下哦，且Matlab的当前文件夹也要是这个目录。
clear;clc
load data_water_quality.mat
%% 注意：如果提示: 错误使用 load，无法读取文件 'data_water_quality.mat'。没有此类文件或目录。
% 那么原因是因为你的Matlab的当前文件夹中不存在这个文件
% 可以使用cd函数修改Matlab的当前文件夹
% 比如说，我的代码和数据放在了: D:第2讲.TOPSIS法（优劣解距离法）\代码和例题数据
% 那么我就可以输入命令：
% cd 'D:第2讲.TOPSIS法（优劣解距离法）\代码和例题数据'
% 也可以看我更新的视频：“更新9_Topsis代码为什么运行失败_得分结果怎么可视化以及权重的确定如何更加准确”，里面有介绍

%%  第二步：判断是否需要正向化
[n,m] = size(X);
disp(['共有' num2str(n) '个评价对象, ' num2str(m) '个评价指标']) 
Judge = input(['这' num2str(m) '个指标是否需要经过正向化处理，需要请输入1 ，不需要输入0：  ']);

if Judge == 1
    Position = input('请输入需要正向化处理的指标所在的列，例如第2、3、6三列需要处理，那么你需要输入[2,3,6]： '); %[2,3,4]
    disp('请输入需要处理的这些列的指标类型（1：极小型， 2：中间型， 3：区间型） ')
    Type = input('例如：第2列是极小型，第3列是区间型，第6列是中间型，就输入[1,3,2]：  '); %[2,1,3]
    % 注意，Position和Type是两个同维度的行向量
    for i = 1 : size(Position,2)  %这里需要对这些列分别处理，因此我们需要知道一共要处理的次数，即循环的次数
        X(:,Position(i)) = Positivization(X(:,Position(i)),Type(i),Position(i));
    % Positivization是我们自己定义的函数，其作用是进行正向化，其一共接收三个参数
    % 第一个参数是要正向化处理的那一列向量 X(:,Position(i))   回顾上一讲的知识，X(:,n)表示取第n列的全部元素
    % 第二个参数是对应的这一列的指标类型（1：极小型， 2：中间型， 3：区间型）
    % 第三个参数是告诉函数我们正在处理的是原始矩阵中的哪一列
    % 该函数有一个返回值，它返回正向化之后的指标，我们可以将其直接赋值给我们原始要处理的那一列向量
    end
    disp('正向化后的矩阵 X =  ')
    disp(X)
end

%% 第三步：对正向化后的矩阵进行标准化
Z = X ./ repmat(sum(X.*X) .^ 0.5, n, 1);
disp('标准化矩阵 Z = ')
disp(Z)

%% 第四步：计算与最大值的距离和最小值的距离，并算出得分
D_P = sum([(Z - repmat(max(Z),n,1)) .^ 2 ],2) .^ 0.5;   % D+ 与最大值的距离向量
D_N = sum([(Z - repmat(min(Z),n,1)) .^ 2 ],2) .^ 0.5;   % D- 与最小值的距离向量
S = D_N ./ (D_P+D_N);    % 未归一化的得分
disp('最后的得分为：')
stand_S = S / sum(S)
[sorted_S,index] = sort(stand_S ,'descend')

% A = magic(5)  % 幻方矩阵
% M = magic(n)返回由1到n^2的整数构成并且总行数和总列数相等的n×n矩阵。阶次n必须为大于或等于3的标量。
% sort(A)若A是向量不管是列还是行向量，默认都是对A进行升序排列。sort(A)是默认的升序，而sort(A,'descend')是降序排序。
% sort(A)若A是矩阵，默认对A的各列进行升序排列
% sort(A,dim)
% dim=1时等效sort(A)
% dim=2时表示对A中的各行元素升序排列
% A = [2,1,3,8]
% Matlab中给一维向量排序是使用sort函数：sort（A），排序是按升序进行的，其中A为待排序的向量；
% 若欲保留排列前的索引，则可用 [sA,index] = sort(A,'descend') ，排序后，sA是排序好的向量，index是向量sA中对A的索引。
% sA  =  8     3     2     1
% index =  4     3     1     2

---

4.Positivization文件

% function [输出变量] = 函数名称(输入变量）  
% 函数的中间部分都是函数体
% 函数的最后要用end结尾
% 输出变量和输入变量可以有多个，用逗号隔开
% function [a,b,c]=test(d,e,f)
%     a=d+e;
%     b=e+f;
%     c=f+d;
% end
% 自定义的函数要单独放在一个m文件中，不可以直接放在主函数里面（和其他大多数语言不同）

function [posit_x] = Positivization(x,type,i)
% 输入变量有三个：
% x：需要正向化处理的指标对应的原始列向量
% type： 指标的类型（1：极小型， 2：中间型， 3：区间型）
% i: 正在处理的是原始矩阵中的哪一列
% 输出变量posit_x表示：正向化后的列向量
    if type == 1  %极小型
        disp(['第' num2str(i) '列是极小型，正在正向化'] )
        posit_x = Min2Max(x);  %调用Min2Max函数来正向化
        disp(['第' num2str(i) '列极小型正向化处理完成'] )
        disp('~~~~~~~~~~~~~~~~~~~~分界线~~~~~~~~~~~~~~~~~~~~')
    elseif type == 2  %中间型
        disp(['第' num2str(i) '列是中间型'] )
        best = input('请输入最佳的那一个值： ');
        posit_x = Mid2Max(x,best);
        disp(['第' num2str(i) '列中间型正向化处理完成'] )
        disp('~~~~~~~~~~~~~~~~~~~~分界线~~~~~~~~~~~~~~~~~~~~')
    elseif type == 3  %区间型
        disp(['第' num2str(i) '列是区间型'] )
        a = input('请输入区间的下界： ');
        b = input('请输入区间的上界： '); 
        posit_x = Inter2Max(x,a,b);
        disp(['第' num2str(i) '列区间型正向化处理完成'] )
        disp('~~~~~~~~~~~~~~~~~~~~分界线~~~~~~~~~~~~~~~~~~~~')
    else
        disp('没有这种类型的指标，请检查Type向量中是否有除了1、2、3之外的其他值')
    end
end

---

5.Inter2Max文件

function [posit_x] = Inter2Max(x,a,b)
    r_x = size(x,1);  % row of x 
    M = max([a-min(x),max(x)-b]);
    posit_x = zeros(r_x,1);   %zeros函数用法: zeros(3)  zeros(3,1)  ones(3)
    % 初始化posit_x全为0  初始化的目的是节省处理时间
    for i = 1: r_x
        if x(i) < a
           posit_x(i) = 1-(a-x(i))/M;
        elseif x(i) > b
           posit_x(i) = 1-(x(i)-b)/M;
        else
           posit_x(i) = 1;
        end
    end
end

---

6.Mid2Max文件

function [posit_x] = Mid2Max(x,best)
    M = max(abs(x-best));
    posit_x = 1 - abs(x-best) / M;
end

---

7.Min2Max文件

function [posit_x] = Min2Max(x)
    posit_x = max(x) - x;
     %posit_x = 1 ./ x;    %如果x全部都大于0，也可以这样正向化
end

---

答案

正向化后的矩阵 X = ?
? ? 4.6900 ? ?0.7172 ? ?3.0000 ? ?1.0000
? ? 2.0300 ? ?0.4069 ? 35.0000 ? ?0.6940
? ? 9.1100 ? ?0.5241 ? ?8.0000 ? ?0.9058
? ? 8.6100 ? ?0.9655 ? ?8.0000 ? ?0.4443
? ? 7.1300 ? ?0.6552 ? ?4.0000 ? ?0.6914
? ? 2.3900 ? ?0.8414 ? 16.0000 ? ?0.6007
? ? 7.6900 ? ?0.8552 ? 16.0000 ? ?0.6551
? ? 9.3000 ? ?0.8690 ? 27.0000 ? ? ? ? 0
? ? 5.4500 ? ?0.5724 ? 49.0000 ? ?1.0000
? ? 6.1900 ? ?0.8138 ? 37.0000 ? ?0.7848
? ? 7.9300 ? ?0.6345 ? 45.0000 ? ?0.6992
? ? 4.4000 ? ?0.8069 ? 37.0000 ? ?0.5419
? ? 7.4600 ? ?0.1448 ? 31.0000 ? ?1.0000
? ? 2.0100 ? ? ? ? 0 ? ?7.0000 ? ?0.4546
? ? 2.0400 ? ?0.5862 ? 31.0000 ? ?1.0000
? ? 7.7300 ? ?0.4069 ? ?2.0000 ? ?1.0000
? ? 6.3500 ? ?0.6000 ? 29.0000 ? ?0.1824
? ? 8.2900 ? ?0.0276 ? 15.0000 ? ?1.0000
? ? 3.5400 ? ?0.8138 ? ? ? ? 0 ? ?0.4088
? ? 7.4400 ? ?0.4897 ? 46.0000 ? ?0.2731

标准化矩阵 Z =?
? ? 0.1622 ? ?0.2483 ? ?0.0245 ? ?0.3065
? ? 0.0702 ? ?0.1408 ? ?0.2863 ? ?0.2127
? ? 0.3150 ? ?0.1814 ? ?0.0655 ? ?0.2776
? ? 0.2977 ? ?0.3342 ? ?0.0655 ? ?0.1361
? ? 0.2466 ? ?0.2268 ? ?0.0327 ? ?0.2119
? ? 0.0826 ? ?0.2912 ? ?0.1309 ? ?0.1841
? ? 0.2659 ? ?0.2960 ? ?0.1309 ? ?0.2008
? ? 0.3216 ? ?0.3008 ? ?0.2209 ? ? ? ? 0
? ? 0.1885 ? ?0.1981 ? ?0.4009 ? ?0.3065
? ? 0.2141 ? ?0.2817 ? ?0.3027 ? ?0.2405
? ? 0.2742 ? ?0.2196 ? ?0.3682 ? ?0.2143
? ? 0.1522 ? ?0.2793 ? ?0.3027 ? ?0.1661
? ? 0.2580 ? ?0.0501 ? ?0.2536 ? ?0.3065
? ? 0.0695 ? ? ? ? 0 ? ?0.0573 ? ?0.1393
? ? 0.0705 ? ?0.2029 ? ?0.2536 ? ?0.3065
? ? 0.2673 ? ?0.1408 ? ?0.0164 ? ?0.3065
? ? 0.2196 ? ?0.2077 ? ?0.2373 ? ?0.0559
? ? 0.2867 ? ?0.0095 ? ?0.1227 ? ?0.3065
? ? 0.1224 ? ?0.2817 ? ? ? ? 0 ? ?0.1253
? ? 0.2573 ? ?0.1695 ? ?0.3763 ? ?0.0837

最后的得分为：

stand_S =

? ? 0.0451
? ? 0.0478
? ? 0.0485
? ? 0.0488
? ? 0.0431
? ? 0.0448
? ? 0.0539
? ? 0.0510
? ? 0.0681
? ? 0.0684
? ? 0.0702
? ? 0.0591
? ? 0.0527
? ? 0.0192
? ? 0.0533
? ? 0.0434
? ? 0.0466
? ? 0.0438
? ? 0.0358
? ? 0.0565

sorted_S =

? ? 0.0702
? ? 0.0684
? ? 0.0681
? ? 0.0591
? ? 0.0565
? ? 0.0539
? ? 0.0533
? ? 0.0527
? ? 0.0510
? ? 0.0488
? ? 0.0485
? ? 0.0478
? ? 0.0466
? ? 0.0451
? ? 0.0448
? ? 0.0438
? ? 0.0434
? ? 0.0431
? ? 0.0358
? ? 0.0192

index =

? ? 11
? ? 10
? ? ?9
? ? 12
? ? 20
? ? ?7
? ? 15
? ? 13
? ? ?8
? ? ?4
? ? ?3
? ? ?2
? ? 17
? ? ?1
? ? ?6
? ? 18
? ? 16
? ? ?5
? ? 19
? ? 14

---

8.增加权重之后的topsis

主要修改的就是步骤二之后添加了一个输入权重的过程，以及步骤四要乘以权重

%%  第一步：把数据复制到工作区，并将这个矩阵命名为X
% （1）在工作区右键，点击新建（Ctrl+N)，输入变量名称为X
% （2）在Excel中复制数据，再回到Matlab中右键，点击粘贴Excel数据（Ctrl+Shift+V）
% （3）关掉这个窗口，点击X变量，右键另存为，保存为mat文件（下次就不用复制粘贴了，只需使用load命令即可加载数据）
% （4）注意，代码和数据要放在同一个目录下哦，且Matlab的当前文件夹也要是这个目录。
clear;clc
load data_water_quality.mat
%% 注意：如果提示: 错误使用 load，无法读取文件 'data_water_quality.mat'。没有此类文件或目录。
% 那么原因是因为你的Matlab的当前文件夹中不存在这个文件
% 可以使用cd函数修改Matlab的当前文件夹
% 比如说，我的代码和数据放在了: D:第2讲.TOPSIS法（优劣解距离法）\代码和例题数据
% 那么我就可以输入命令：
% cd 'D:第2讲.TOPSIS法（优劣解距离法）\代码和例题数据'
% 也可以看我更新的视频：“更新9_Topsis代码为什么运行失败_得分结果怎么可视化以及权重的确定如何更加准确”，里面有介绍

%%  第二步：判断是否需要正向化
[n,m] = size(X);
disp(['共有' num2str(n) '个评价对象, ' num2str(m) '个评价指标']) 
Judge = input(['这' num2str(m) '个指标是否需要经过正向化处理，需要请输入1 ，不需要输入0：  ']);

if Judge == 1
    Position = input('请输入需要正向化处理的指标所在的列，例如第2、3、6三列需要处理，那么你需要输入[2,3,6]： '); %[2,3,4]
    disp('请输入需要处理的这些列的指标类型（1：极小型， 2：中间型， 3：区间型） ')
    Type = input('例如：第2列是极小型，第3列是区间型，第6列是中间型，就输入[1,3,2]：  '); %[2,1,3]
    % 注意，Position和Type是两个同维度的行向量
    for i = 1 : size(Position,2)  %这里需要对这些列分别处理，因此我们需要知道一共要处理的次数，即循环的次数
        X(:,Position(i)) = Positivization(X(:,Position(i)),Type(i),Position(i));
    % Positivization是我们自己定义的函数，其作用是进行正向化，其一共接收三个参数
    % 第一个参数是要正向化处理的那一列向量 X(:,Position(i))   回顾上一讲的知识，X(:,n)表示取第n列的全部元素
    % 第二个参数是对应的这一列的指标类型（1：极小型， 2：中间型， 3：区间型）
    % 第三个参数是告诉函数我们正在处理的是原始矩阵中的哪一列
    % 该函数有一个返回值，它返回正向化之后的指标，我们可以将其直接赋值给我们原始要处理的那一列向量
    end
    disp('正向化后的矩阵 X =  ')
    disp(X)
end
%% 作业：在这里增加是否需要算加权
% 补充一个基础知识：m*n维的矩阵A 点乘 n维行向量B，等于这个A的每一行都点乘B
% （注意：2017以及之后版本的Matlab才支持，老版本Matlab会报错）
% % 假如原始数据为：
%   A=[1, 2, 3;
%        2, 4, 6] 
% % 权重矩阵为：
%   B=[ 0.2, 0.5 ,0.3 ] 
% % 加权后为：
%   C=A .* B
%     0.2000    1.0000    0.9000
%     0.4000    2.0000    1.8000
% 类似的，还有矩阵和向量的点除， 大家可以自己试试计算A ./ B
% 注意，矩阵和向量没有 .- 和 .+ 哦 ，大家可以试试，如果计算A.+B 和 A.-B会报什么错误。

%% 这里补充一个小插曲
% % 在上一讲层次分析法的代码中，我们可以优化以下的语句：
% % Sum_A = sum(A);
% % SUM_A = repmat(Sum_A,n,1);
% % Stand_A = A ./ SUM_A;
% % 事实上，我们把第三行换成：Stand_A = A ./ Sum_A; 也是可以的哦 
% % (再次强调，新版本的Matlab才能运行哦)

%% 让用户判断是否需要增加权重
disp('请输入是否需要增加权重向量，需要输入1，不需要输入0')
Judge = input('请输入是否需要增加权重： ');
if Judge == 1
    disp(['如果你有3个指标，你就需要输入3个权重，例如它们分别为0.25,0.25,0.5, 则你需要输入[0.25,0.25,0.5]']);
    weigh = input(['你需要输入' num2str(m) '个权数。' '请以行向量的形式输入这' num2str(m) '个权重: ']);
    OK = 0;  % 用来判断用户的输入格式是否正确
    while OK == 0 
        if abs(sum(weigh) - 1)<0.000001 && size(weigh,1) == 1 && size(weigh,2) == m   % 这里要注意浮点数的运算是不精准的。
             OK =1;
        else
            weigh = input('你输入的有误，请重新输入权重行向量: ');
        end
    end
else
    weigh = ones(1,m) ./ m ; %如果不需要加权重就默认权重都相同，即都为1/m
end


%% 第三步：对正向化后的矩阵进行标准化
Z = X ./ repmat(sum(X.*X) .^ 0.5, n, 1);
disp('标准化矩阵 Z = ')
disp(Z)

%% 第四步：计算与最大值的距离和最小值的距离，并算出得分
D_P = sum([(Z - repmat(max(Z),n,1)) .^ 2 ] .* repmat(weigh,n,1) ,2) .^ 0.5;   % D+ 与最大值的距离向量
D_N = sum([(Z - repmat(min(Z),n,1)) .^ 2 ] .* repmat(weigh,n,1) ,2) .^ 0.5;   % D- 与最小值的距离向量
S = D_N ./ (D_P+D_N);    % 未归一化的得分
disp('最后的得分为：')
stand_S = S / sum(S)
[sorted_S,index] = sort(stand_S ,'descend')

% A = magic(5)  % 幻方矩阵
% M = magic(n)返回由1到n^2的整数构成并且总行数和总列数相等的n×n矩阵。阶次n必须为大于或等于3的标量。
% sort(A)若A是向量不管是列还是行向量，默认都是对A进行升序排列。sort(A)是默认的升序，而sort(A,'descend')是降序排序。
% sort(A)若A是矩阵，默认对A的各列进行升序排列
% sort(A,dim)
% dim=1时等效sort(A)
% dim=2时表示对A中的各行元素升序排列
% A = [2,1,3,8]
% Matlab中给一维向量排序是使用sort函数：sort（A），排序是按升序进行的，其中A为待排序的向量；
% 若欲保留排列前的索引，则可用 [sA,index] = sort(A,'descend') ，排序后，sA是排序好的向量，index是向量sA中对A的索引。
% sA  =  8     3     2     1
% index =  4     3     1     2

---

5.模型扩展

1.问题引出

计算得分时的操作

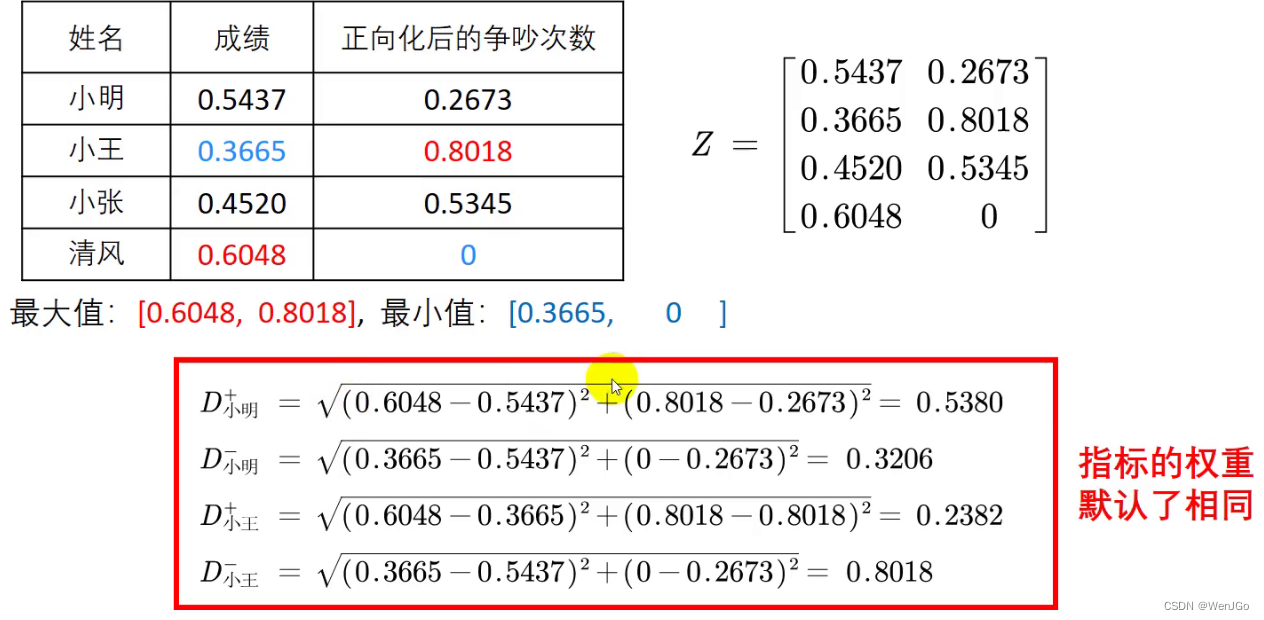
这样操作就是默认了两个的权重是相同的，但是实际上不同的指标权重应该是不相同的。

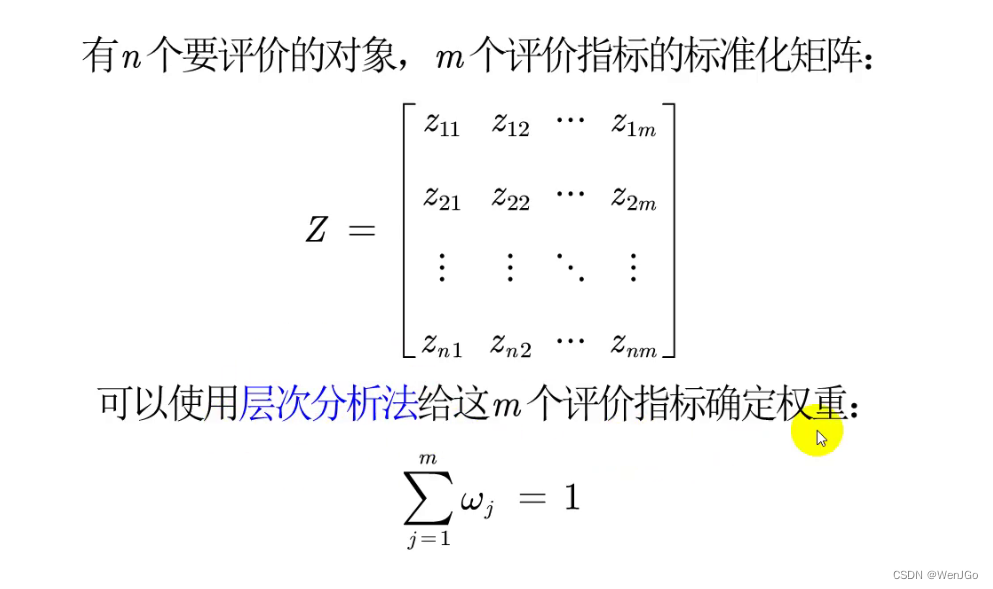
2.带权重的TOPSIS

可以使用层次分析法带上权重

---

结语

要什么结语，累死了，又是一篇文章写一天的一天，ffff！！！！