[ACM学习]自上而下树形dp

问题引入

设置dp状态，相比于更容易出错的贪心更...不易出错。

状态设计

如果选择父结点，就会使孩子结点不能被选择，我们会多开一维的dp，用来标记该点是否被标记过。

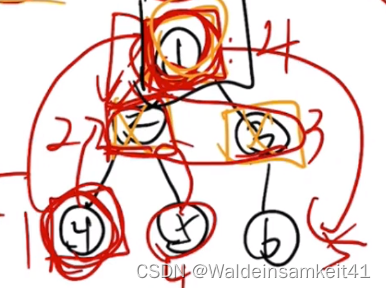
以1点举例，f[1][0]为不选它的状态，那么它的子结点2 3 是可选可不选的，所以是 max(f[2][0],f[2][1])+max(f[3][0]+f[3][1]) ，在子结点的两个状态里挑最大值，并且子结点间没有限制，所以直接相加。

f[1][1]=f[2][0]+f[3][0]

所以这题的总体思路是：从叶子结点开始，dp[v][0]=0?dp[v][1]=a_v，并且到达根。

最后结果在 dp[root][0] dp[root][0]里挑一个max

void dfs(int u, int fa)
{
    for (int i = head[u]; i; i = edge[i].nex)
    {
        int v = edge[i].to;
        if (v != fa)
            continue;
        dfs(v, u);
        f[u][0] += max(f[v][0], f[v][1]);
        f[u][1] += f[v][0];
    }
    return ;
}

在这里解释一下自上而上：父结点的状态转移方程是会受到孩子状态值的影响。算法进行的方向还是从叶子计算到根。

问题二

状态设计

二维可以解决，将是否选择这个点并入体积里（选了这个点即为多这个点的体积）

状态转移是什么样的？可以把一个子树的几个孩子看成是几个物品，用类似于背包问题进行状态转移。

当前结点u在体积v1下，由体积v1-v2下加上某一孩子的v2体积下价值与它原来的值进行大小对比。所以我们会对v1 v2进行枚举。

虽然我们类比了01背包，但是和01背包问题相比，某一个子树的体积不是某个定值，而是会从0到最大限度进行枚举。

void dfs(int u, int fa)
{
    memset(f[u], -0x3f, sizeof f[u]);
    if (v[u] <= V)
        f[u][v[u]] = w[u];  //把当前结点放进去，以u为根的子树里，还只放入了结点u
    for (int i = head[u]; i; i = edge[i].nex)   //枚举每一个子树
    {
        int v = edge[i].to;
        if (v == fa)
            continue;
        dfs(v, u);  
   //从叶子开始，
    //，每个孩子结点看成不同的物品，进行01背包
        vector<int> nf(f[u], f[u] + V + 1);  //当前子树的背包过程，用来转移
        for (int v1 = 0; v1 <= V; v1 ++)   //含义：在放入这个子树前，已使用的体积
        {
            for (int v2 = 0; v1 + v2 <= V; v2 ++ )  //放入v2后不能超过V
            {
                nf[v1 + v2] = max(nf[v1 + v2], f[u][v1] + f[v][v2]);
            }
        }
        for (int v = 0; v <= V; v ++ )
            f[u][v] = nf[v];
    }
    return ;
}

问题二进阶

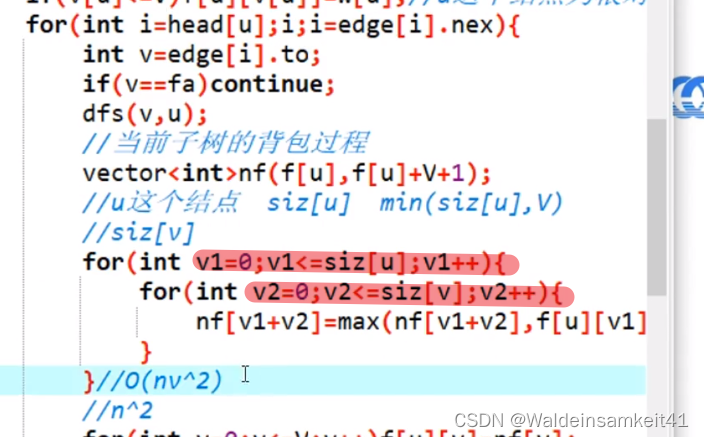
siz[u] 是指，把包含u在内，u为根的子树，把所有权值都加上，得到的和。

虽然还是两层for，但是如果在每个结点都体积为1的情况下，相当于是把以u为子树的每个结点两两进行比较。