【格密码】如何解决BDD问题

目录

一. 铺垫

二. 随机的BDD算法

2.1 介绍

2.2. 格上高斯采样解码

2.3 找最近的格点

2.4 小结

三. 本文用到的缩写

四. 推荐阅读

---

推荐先阅读：

基于格密码的无线通信MIMO系统-CSDN博客

一. 铺垫

BDD：Bounded Distance Decoding 有限距离解码

将格基B进行Gram-Schmidt正交化后的向量记为：

向量垂直于向量空间的分量即为。有关格基正交化的性质，可参考：

格密码基础：最短向量与连续最小值（附下界讨论）_格点都是离散的-CSDN博客

将格基矩阵进行QR分解：

其中Q为正交矩阵，第i列记为向量。R为上三角矩阵，第i个对角线处的元素记为。实际上正交化的过程和矩阵QR分解之间是有关系的，如下：

如果向量点y和格L的距离小于最短的Gram-Schmidt向量一半（相当于对BDD距离的限制），利用串行干扰消除的方法（SIC），则可找到离其最近的格点。这个时候正确的解码半径（correct decoding radius）为：

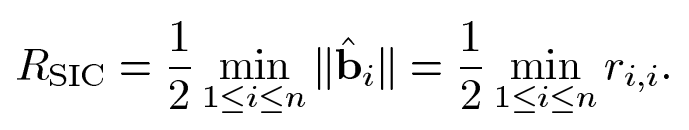
格密码中最短的向量长度叫，对应的正确解码半径为。如果放在MIMO里面，这就是无限解码（ILD）。

在格密码中解决BDD问题和在MIMO的星座图中解决BDD问题是不一样的，这两者之间的比值可以形成近似因子（proximity factor），如下：

该比值一定是一个有限值，基于格基约化的SIC算法就可以看成BDD问题的一个实例。此处给出格密码中近似BDD问题的定义：

选取一个实数点y，该实数点离最近格点的距离小于：

尝试找出离y最近的格点，则称之为近似BDD问题。

如果离格点的距离很近，则可以直接使用Babai算法和Kannan算法来解决。

那如果噪声项超过了这个解码半径，该怎么办？

我们往下看。

二. 随机的BDD算法

2.1 介绍

接下来介绍的算法最早由Klein提出，他将BDD问题的解码半径优化到了：

其中k的范围如下：

随机化的BDD算法的复杂度为：

可以看到当k为常数时，该算法即为多项式时间复杂度。

我们知道标准的串行干扰消除算法中会用到就近取整，这一步可以进行优化。

2.2. 格上高斯采样解码

将该算法总结为如下伪代码形式：

该算法的输入已经经过的正交矩阵求逆的预处理，也就是：

此处A的取值为：

将以上代码的函数抽象为：

其中c代表一个常数，该函数将输入r随机取整到一个整数Q。该取整过程依据如下高斯分布：

右边的s相当于把所有格点对应的高斯分布值求和。左边的概率相当于把连续的高斯分布扣成一个个离散的点。

其中参数c类似高斯分布的标准差，可以相当，如果c接近无限大的话，那么该分布则接近均匀分布，取整就是正常的就近取整原则；

如果c很小的话，那么取整则寻找概率最大的格点。

s的取值有一个上限，如下：

2.3 找最近的格点

假定z是L(B)的格点，y为任意内的实数点。根据Klein算法（又叫做Rand_SIC算法），取得格点z的概率可以计算为：

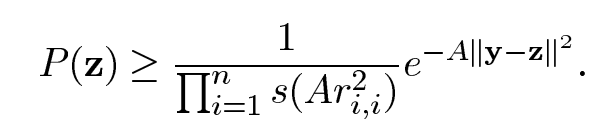
其中s为与c相关的参数，c的值在每个维度上都不一样，取值为：

其中：

为格基矩阵B分离出的对角线元素。

这样我们就可以确定取哪个格点的概率更大，从而选择最合适的格点。

证明：

将格点z表示为：

其中为整数。

接着调用以上伪代码的程序，我们希望：

满足该情况的概率为：

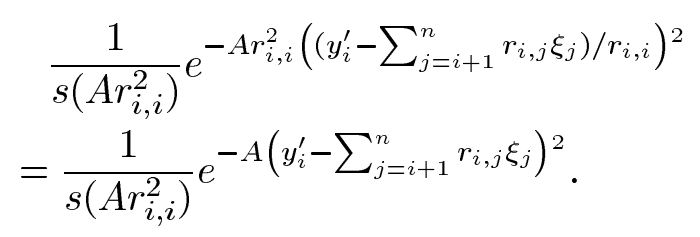
等号代表把对角线处的元素带入。

一共有n维，同时满足则要求相乘，可得：

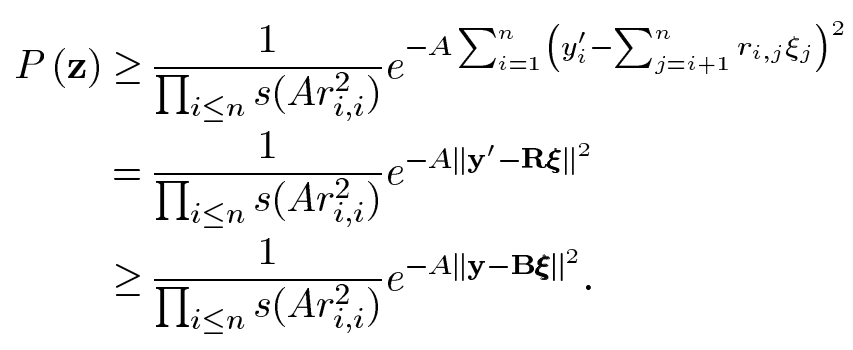
对我们来讲有用的就是最终的结论。注意指数位置就是z。

证明完毕。

2.4 小结

以上推导说明最近的格点很有可能会被取到，而且取到的概率类似格上高斯分布。当抽样的格点z离y越近时，概率下限越大。

综上当时，取得格点的概率为：

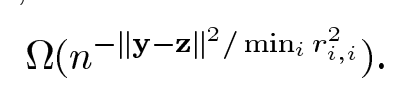
格基约化在此步也可以使用。可以发现当增大r的值时，该概率也在增大。

反应在实际应用中时，格点可能不是无限的，比如无线网络安全的MIMO模型中，解出来的格点可能位于星座图的外面。此时借助硬极限（hard-limiting）可解决此问题。

将以上思路应用于迫零算法（ZF）也是适用的，但其性能不如SIC。

三. 本文用到的缩写

MIMO：Multiple Input Multiple Output?多输入多输出天线

ZF：zero-forcing 迫零算法

SIC：successive interference cancellation?串行干扰消除

BDD：Bounded Distance Decoding 有限距离解码

L：lattice 格

四. 推荐阅读

（1）串行干扰消除和基于格解决BDD

C. Ling, “On the proximity factors of lattice reduction-aided decoding,” IEEE Trans. Signal Process., vol. 59, no. 6, pp. 2795–2808, Jun. 2011.

（2）利用随机化的SIC算法解决BDD

P. Klein, “Finding the closest lattice vector when it’s unusually close,” in Proc. ACM-SIAM Symp. Discr. Algorithms, 2000, pp. 937–941.
?