代码随想录刷题总结--栈和队列
232.用栈实现队列
使用栈实现队列的下列操作:
push(x) -- 将一个元素放入队列的尾部。 pop() -- 从队列首部移除元素。 peek() -- 返回队列首部的元素。 empty() -- 返回队列是否为空。
思路
-
栈的特点先进后出,队列则是先进先出,因此要用先进后出的的特点去实现先进先出
-
明显使用一个栈无法满足 ,使用2个栈,一个存放进入队列的元素,一个存放出队列的元素
-
当进入队列,直接将队列中的元素全部放入一个栈中
-
出队列则将第一个栈中的元素放入 第二个栈中,再弹出,此时先放入的元素,就已经在第二个队列的最前面,就可以实现先进先出的效果

class MyQueue {
?
Stack<Integer> stackIn;
Stack<Integer> stackOut;
?
public MyQueue() {
stackIn = new Stack<Integer>(); //入栈
stackOut = new Stack<Integer>(); //出栈
}
?
public void push(int x){
stackIn.push(x);
}
?
public int pop() {
dumpstackIn();
return stackOut.pop();
}
public int peek() {
dumpstackIn();
return stackOut.peek();
}
public boolean empty() {
return stackIn.isEmpty() && stackOut.isEmpty();
}
?
private void dumpstackIn() {
//当弹出栈不为空 直接取
if (!stackOut.empty()) return;
//当弹入栈为空,则将入栈 的所有元素放入
while (!stackIn.empty()){
stackOut.push(stackIn.pop());
}
}
?
}225. 用队列实现栈
-
push(x) -- 元素 x 入栈
-
pop() -- 移除栈顶元素
-
top() -- 获取栈顶元素
-
empty() -- 返回栈是否为空
思路
-
用队列实现先进后出效果,关键点在于出队列的时候 ,元素顺序需要倒转过来 ,让最后 一个元素变成第一个元素
-
使用一个队列模拟,每当移除元素,先移除队列中的前size-1个元素,然后将前size-1元素进入队列,此时最先进入的元素就在队列的最低前面了,然后移除队列元素
class MyStack {
Queue<Integer> queue1; //和栈中的元素一致
?
public MyStack() {
queue1 = new LinkedList<Integer>();
}
?
public void push(int x) {
queue1.offer(x);
}
?
public int pop() {
//将前size--个元素重新追加到队列后面,使得最后一个元素,最先出队列
int size = queue1.size();
size--;
while (size-- > 0) {
queue1.add(queue1.poll());
}
return queue1.poll();
}
?
public int top() {
//将前size--个元素重新追加到队列后面,使得最后一个元素,最先出队列
int size = queue1.size();
size--;
while (size-- > 0) {
queue1.add(queue1.poll());
}
Integer poll = queue1.poll();
queue1.offer(poll);
return poll;
}
?
public boolean empty() {
return queue1.isEmpty();
}
}20. 有效的括号
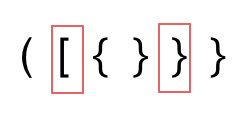
给定一个只包括 '(',')','{','}','[',']' 的字符串,判断字符串是否有效。
有效字符串需满足:
-
左括号必须用相同类型的右括号闭合。
-
左括号必须以正确的顺序闭合。
-
注意空字符串可被认为是有效字符串。
示例 1:
-
输入: "()"
-
输出: true
示例 2:
-
输入: "()[]{}"
-
输出: true
示例 3:
-
输入: "(]"
-
输出: false
.思路
-
可以使用栈,遍历符号,当符号口朝左边,则放入栈中对应的朝向右边的括号 ,当遍历的字符朝向右边,并且匹配则移除元素我匹配成功
-
最终匹配的结果共三种:
-
已经遍历完了字符串,但是栈不为空,说明有相应的左括号没有右括号来匹配,所以return false
-
-
遍历字符串匹配的过程中,发现栈里没有要匹配的字符。所以return false
-
-
遍历字符串匹配的过程中,栈已经为空了,没有匹配的字符了,说明右括号没有找到对应的左括号return false

-
? ?
public boolean isValid(String s) {
Deque<Character> deque = new LinkedList<>();
char ch;
for (int i = 0; i < s.length(); i++) {
ch = s.charAt(i);
if ('(' == s.charAt(i)){
deque.push(')');
}else if ('{' == ch){
deque.push('}');
}else if ('[' == ch){
deque.push(']');
//遍历字符串遇到朝右边的括号,开始匹配
}else if (deque.isEmpty() || ch != deque.peek()){//栈为空则没有匹配到对应的左边元素,情况三,栈顶元素和当前字符串不匹配,说明是有括号封闭的顺序不对
return false;
}else {
//匹配成功则弹栈
deque.pop();
}
?
}
//情况三
if (!deque.isEmpty()){
return false;
}
return true;
}1047. 删除字符串中的所有相邻重复项
示例:
-
输入:"abbaca"
-
输出:"ca"
-
解释:例如,在 "abbaca" 中,我们可以删除 "bb" 由于两字母相邻且相同,这是此时唯一可以执行删除操作的重复项。之后我们得到字符串 "aaca",其中又只有 "aa" 可以执行重复项删除操作,所以最后的字符串为 "ca"。
思路
-
使用栈进行匹配 ,可以新增一个字符串对象作为栈
-
遍历字符串,字符串栈对象,需要另外定义一个指针,当匹配失败则入栈,指针增加,匹配成功则出栈,指针减少一个位置
//将字符串当做栈,遍历 每一个字符和栈顶元素比较 定义一个指针为栈顶
public String removeDuplicates(String s) {
StringBuffer sb = new StringBuffer();
int top = -1;
for (int i = 0; i < s.length(); i++) {
char ch = s.charAt(i);
//栈中有值 并且栈顶元素等予字符串当前遍历的字符
if (top >= 0 && ch == sb.charAt(top)){
sb.deleteCharAt(top);
top--;
}else {
sb.append(ch);
top++;
}
}
return sb.toString();
}?
150. 逆波兰表达式求值
根据 逆波兰表示法,求表达式的值。
有效的运算符包括 + , - , * , / 。每个运算对象可以是整数,也可以是另一个逆波兰表达式。
说明:
整数除法只保留整数部分。 给定逆波兰表达式总是有效的。换句话说,表达式总会得出有效数值且不存在除数为 0 的情况。
示例 1:
-
输入: ["2", "1", "+", "3", " * "]
-
输出: 9
-
解释: 该算式转化为常见的中缀算术表达式为:((2 + 1) * 3) = 9
思路
-
遇到符号则取前两位数字做运算
-
使用栈模拟操作,遍历字符串,遇到数字入栈
-
遇到操作符,取栈顶的两个元素做运算,然后将这两个元素弹出,将运算的结果入栈,一直遍历完字符串
?
public int evalRPN(String[] tokens) {
Deque<Integer> stack = new LinkedList<>();
for (String token : tokens) {
if (token.equals("+")){
stack.push(stack.pop() + stack.pop());
}else if (token.equals("-")){
//减法和除法特殊处理,操作元素是到处第二个元素操作栈顶元素
stack.push(-stack.pop() + stack.pop());
}else if (token.equals("*")){
stack.push(stack.pop() * stack.pop());
}else if (token.equals("/")){
int t1 = stack.pop();
int t2 = stack.pop();
stack.push(t2 / t1);
}else {
stack.push(Integer.valueOf(token));
}
}
return stack.pop();
}347.前 K 个高频元素
给定一个非空的整数数组,返回其中出现频率前 k 高的元素。
示例 1:
-
输入: nums = [1,1,1,2,2,3], k = 2
-
输出: [1,2]
思路
-
统计元素出现频率
-
类似于哈希表的思路,构建一个map,key出现的元素,value为出现的频率
-
-
对频率排序
-
因为需要将map进行排序 ,这里构建优先级队列进行我排序,优先级队列内部元素是自动依照元素的权值排列,默认是根据节点值倒叙排序,即为大顶堆
-
用小顶堆,因为要统计最大前k个元素,只有小顶堆每次将最小的元素弹出,最后小顶堆里积累的才是前k个最大元素
-
public int[] topKFrequent(int[] nums, int k) {
//1.定义一个小顶堆,即为优先级队列 lamda表达 根据数组的第一个元素正序
PriorityQueue<int[]> priorityQueue = new PriorityQueue<>((o1, o2) -> o1[1] - o2[1]);
//2.定义map 和返回数组
int[] ints = new int[k];
Map<Integer,Integer> map = new HashMap<>();
//3.组装map 的key value
for (int num : nums) {
map.put(num,map.getOrDefault(num,0) + 1);
}
//4、将map转为数字存入小顶堆
for (Map.Entry<Integer, Integer> integerIntegerEntry : map.entrySet()) {
int[] temp = new int[2];
temp[0] = integerIntegerEntry.getKey();
temp[1] = integerIntegerEntry.getValue();
priorityQueue.offer(temp);
if (priorityQueue.size() > k){
priorityQueue.poll();
}
}
?
//5、获取小顶堆的key
for (int i = 0; i < k; i++) {
ints[i] = Objects.requireNonNull(priorityQueue.poll())[0];
}
?
return ints;
}本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 程序媛的mac修炼手册--浏览器设置篇Safari vs Chrome
- C语言零基础入门(结构体)
- 鸿鹄电子招投标系统源码实现与立项流程:基于Spring Boot、Mybatis、Redis和Layui的企业电子招采平台
- Mybatis配置入门
- 算法训练营第三十天|332.重新安排行程 51. N皇后 37. 解数独
- 编写系统服务脚本
- matlab appdesigner系列-常用8-坐标区、按钮
- 深入了解ISO 8601:日期和时间的国际标准化
- 大学生未毕业就月均收入5000,原来是做了这些。
- 克魔助手:方便查看iPhone应用实时日志和奔溃日志工具