机器学习之无监督学习

聚类：发掘纵向结构的某种模式信息，某些x属于相同的分布或者类别

特征学习：发掘横向结构的某种模式信息，每一行都可以看成是一种属性或特征

密度估计：发掘底层数据分布，x都是从某个未知分布p(x)采出来的，p(x)是什么，能不能估计出来

聚类

样本间距离

C是指C簇

常见聚类任务

常见聚类方法

聚类效果评估

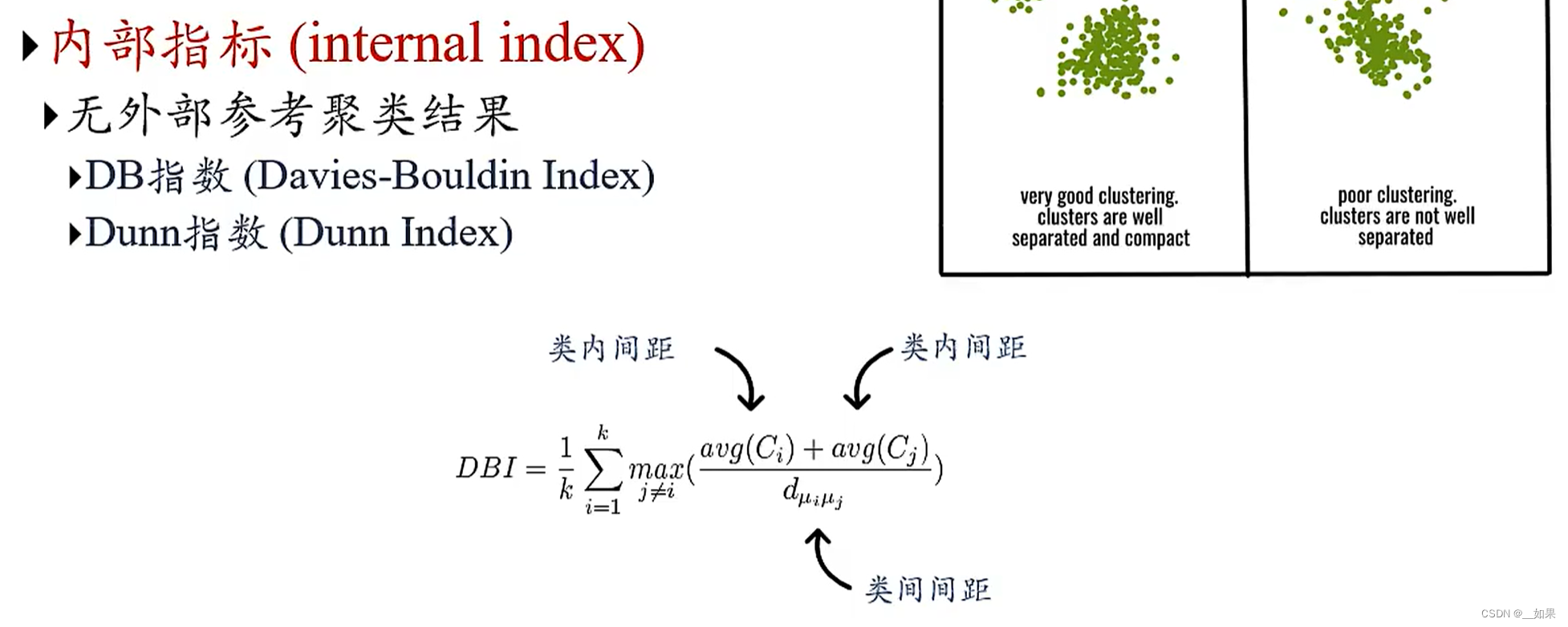
外部指标

内部指标

当我们没有办法参考正确的分类，我们怎么评判聚类的好坏？

最核心的思想还是类内相似度高，类间相似度低

K均值

聚类过程

（1）k是类别的数量，随机选k个点作为类中心

（2）根据每个点到k个类中心的距离划分类别区域

（3）根据区域内的点重新调整类中心

（4）继续迭代

目标函数与优化

μi是类中心，优化的目标是Ci和μi -> 怎么确定x∈Ci与确定每个类的中心μi

超参选择

K

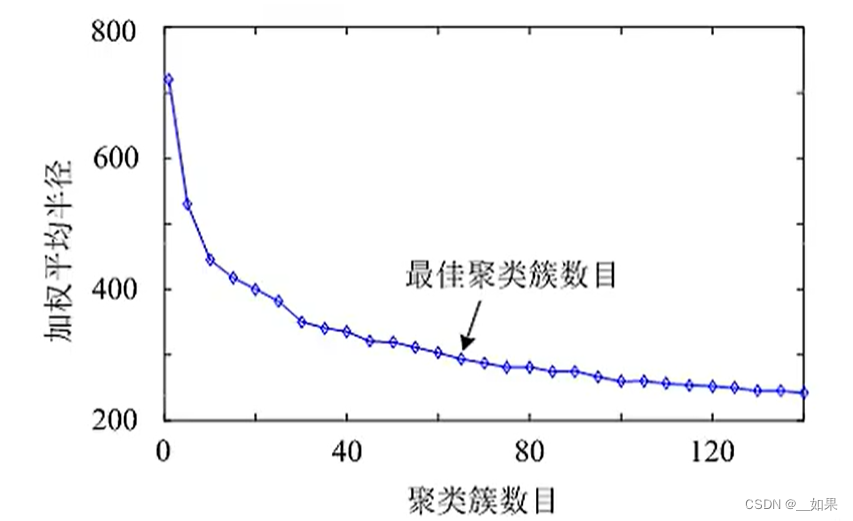
横坐标是K，纵坐标是E，可以看到当你的K足够大的时候，这时每个数据自成一类，E是可以等于0的

最佳的K大致是在过了下降最快的部分选一个就行了，不必要使E太小

类中心初始化

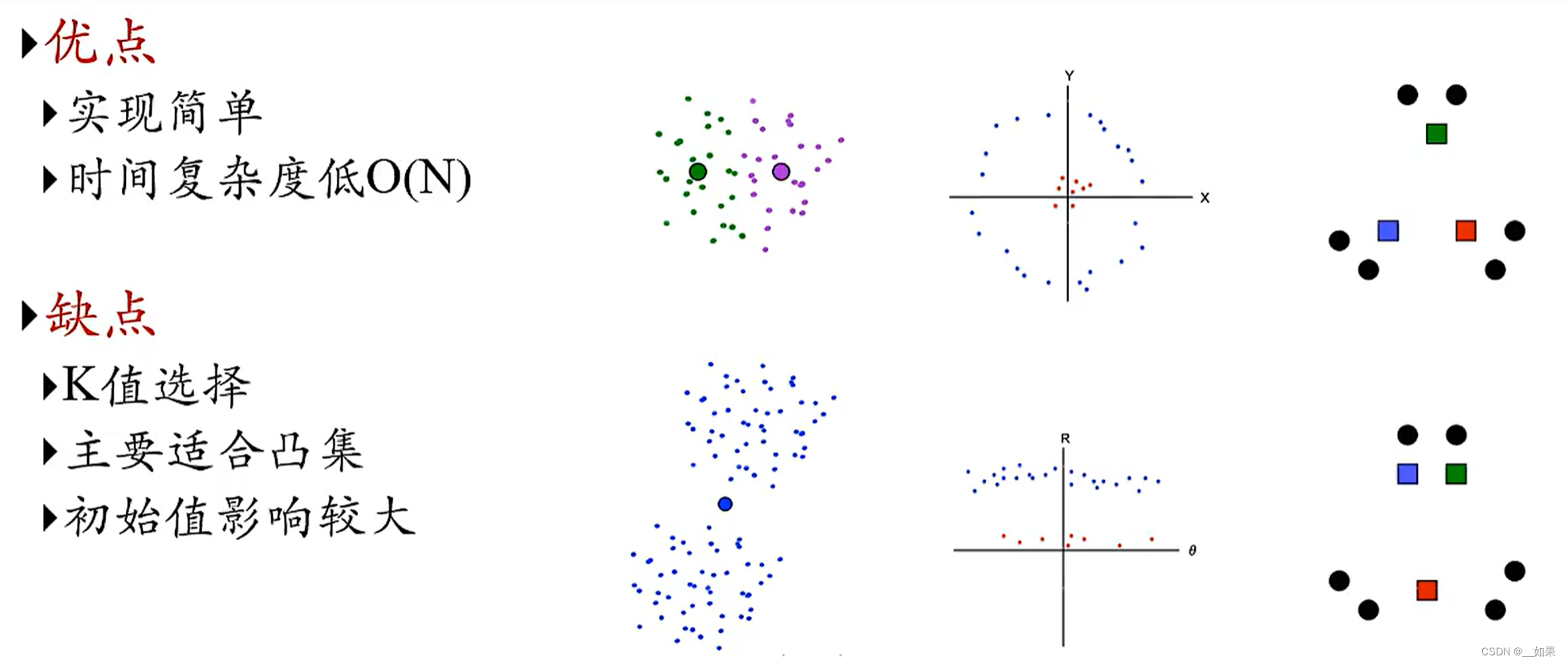
优缺点

层次聚类

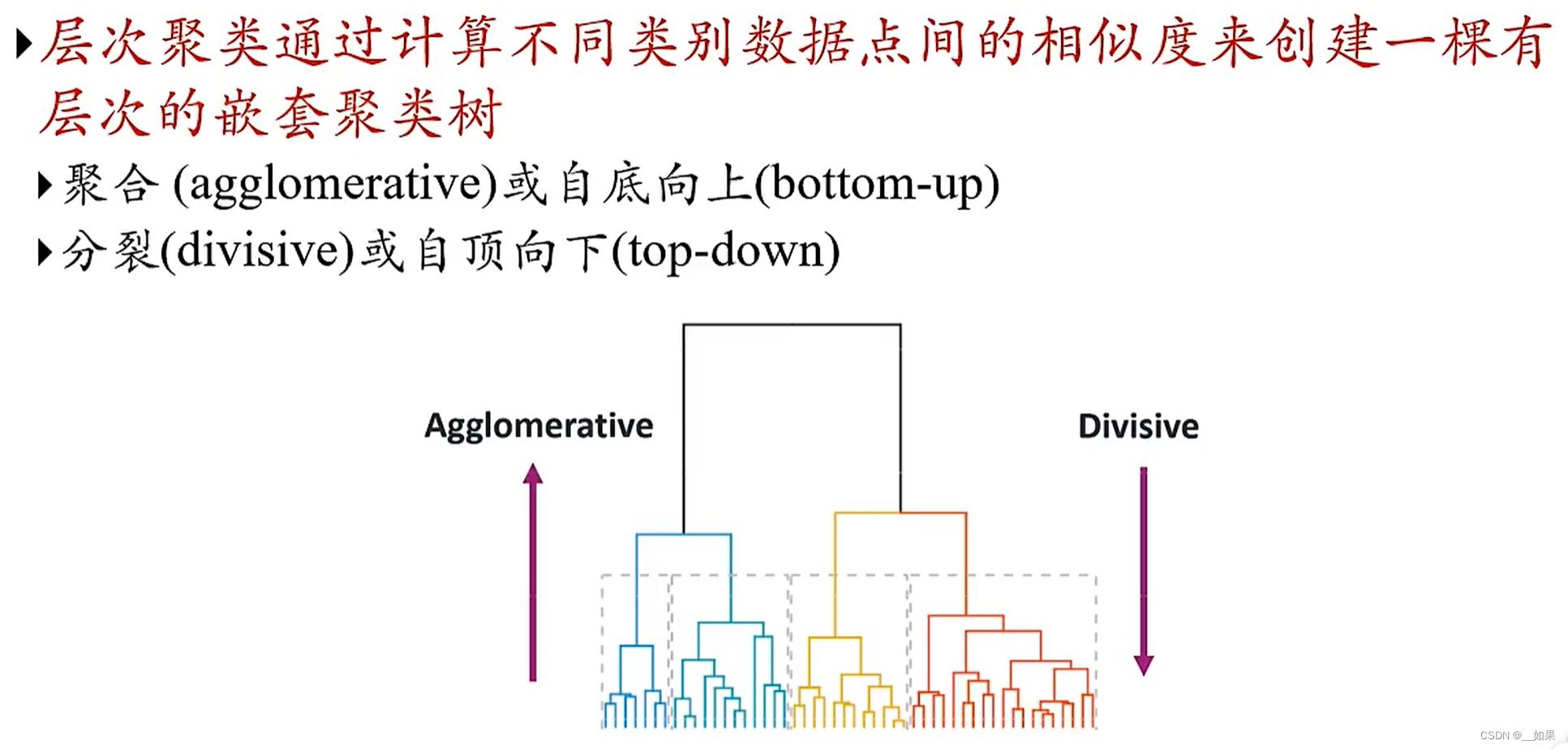
聚合聚类过程

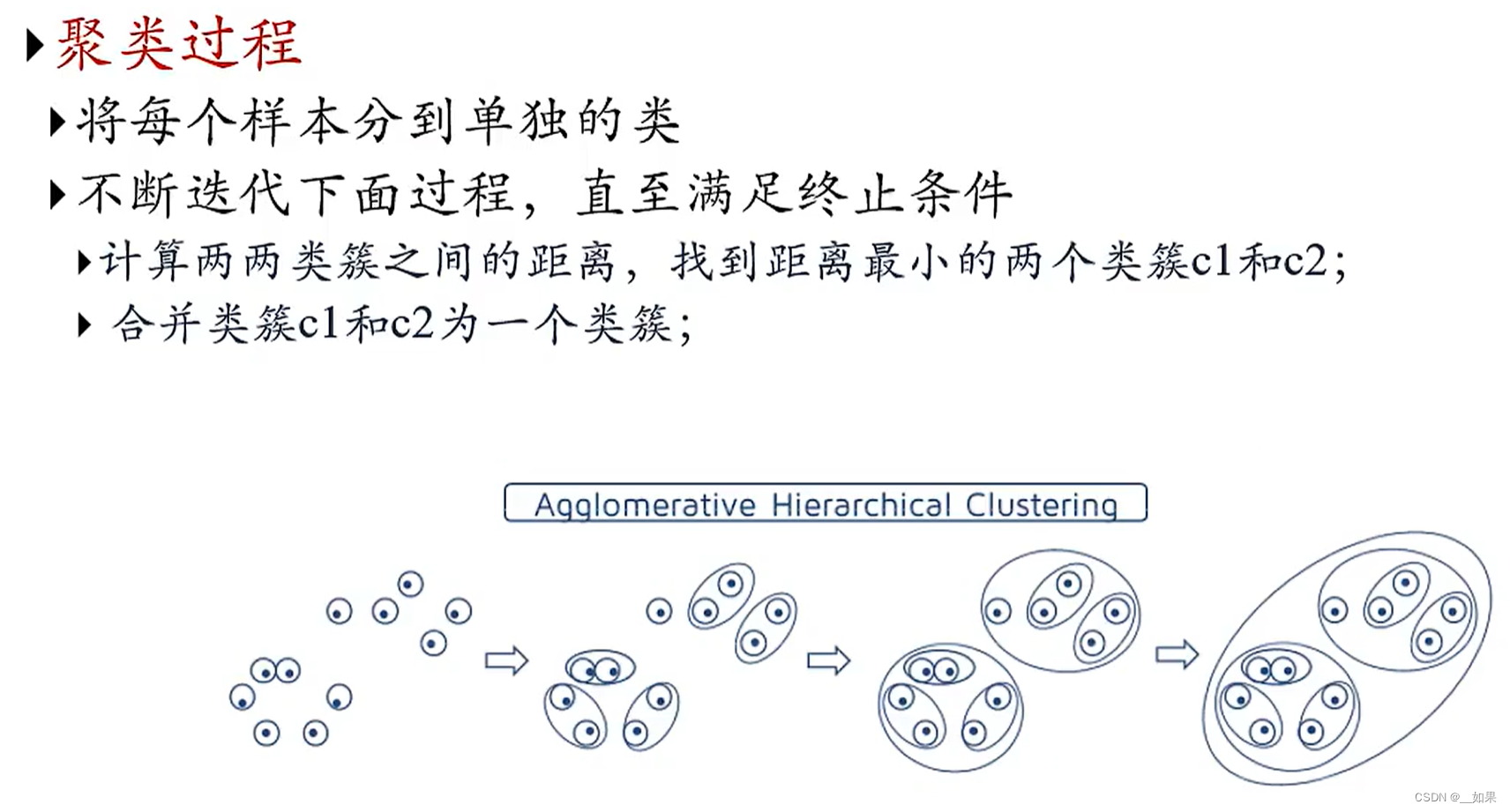
分裂聚类过程

优缺点

无监督特征学习

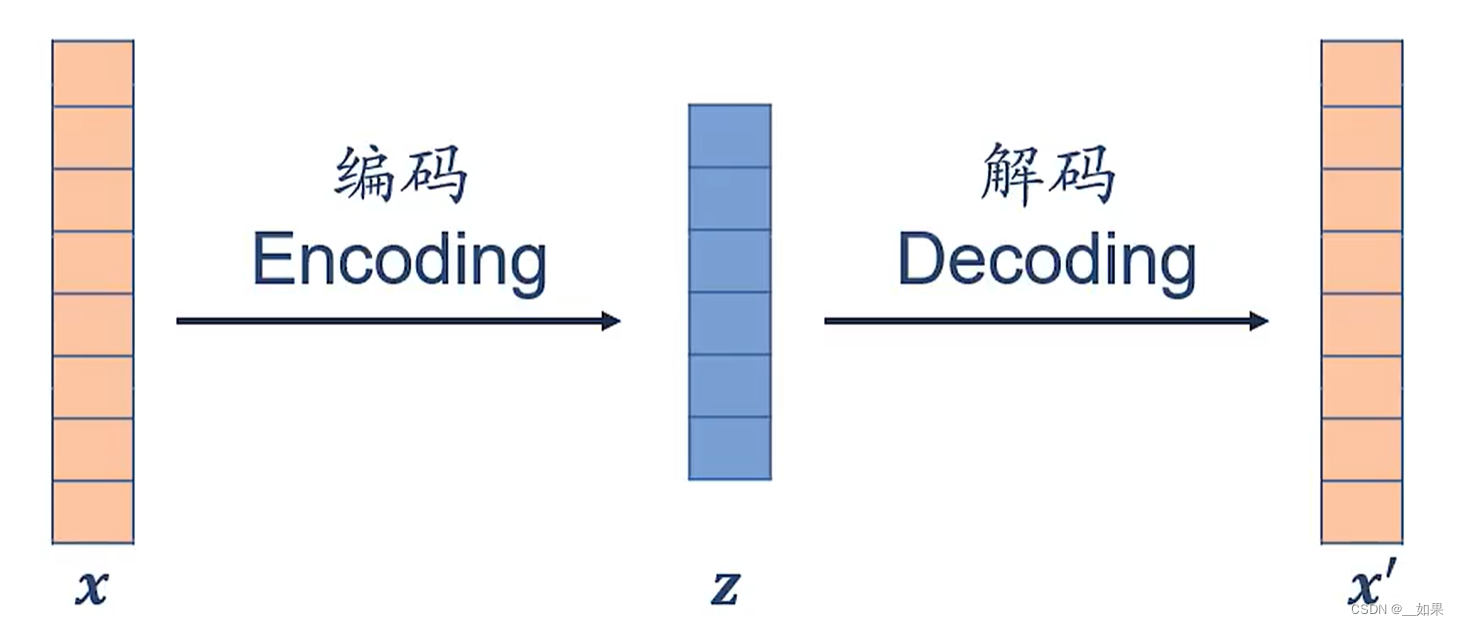
无监督特征学习的目的是从原始的特征空间中学习一种更有用的特征或表示

上面的图是无监督特征学习的完整框架，但在实际应用中不一定需要整套框架，比如我们只需要encoding这部分，PCA是希望数据集投影下来后，在投影空间中方差最大；比如我们只需要后面decoding这部分，我们希望直接通过数据集的迭代学到一个z，使得z可以作为某种x的有效编码

应用

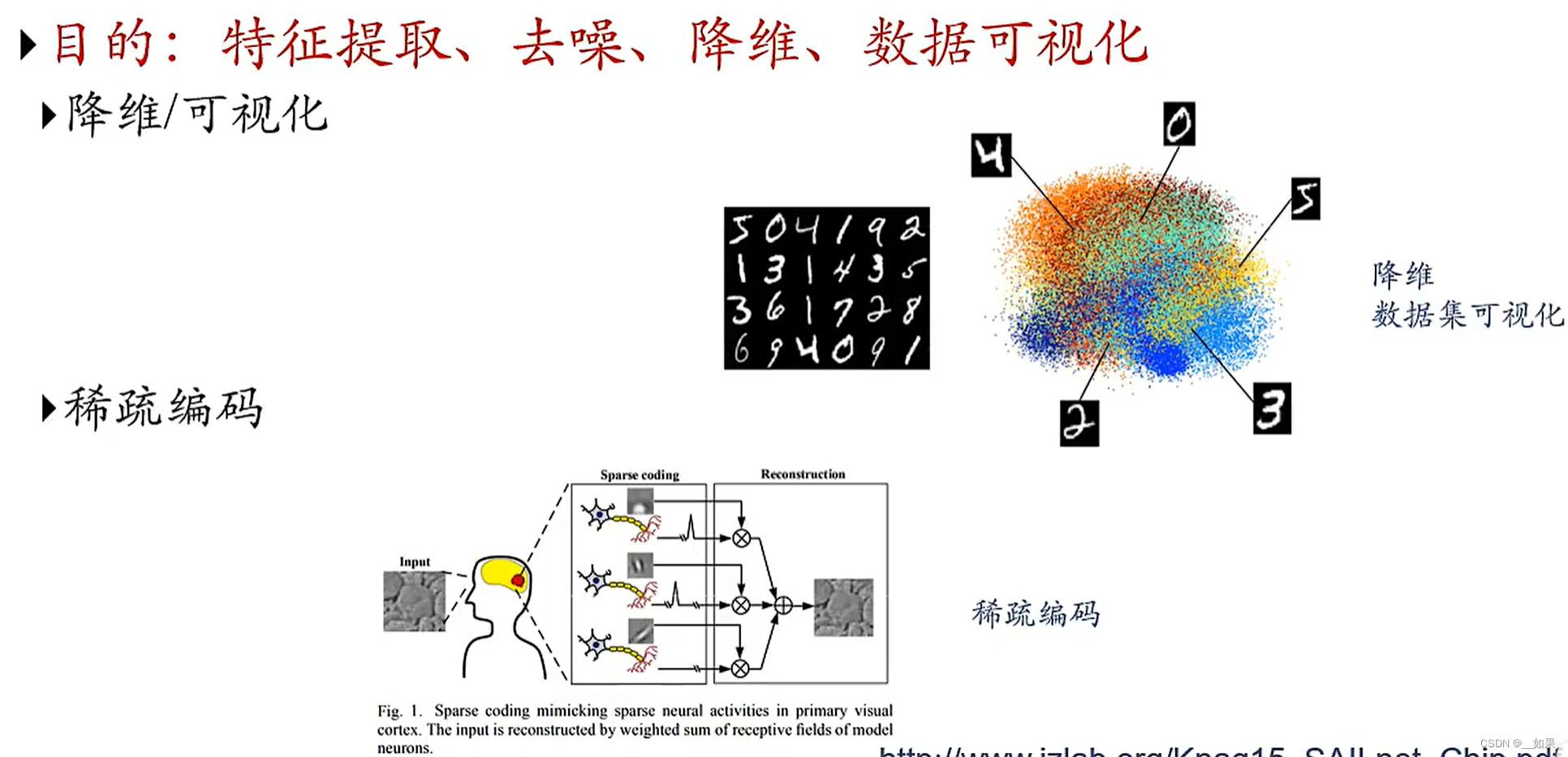
稀疏编码：人脑读取一张图片是某种稀疏激活，可以用少量的信息表示这幅图。相当于一个高维信息进来，我们可能只用少量的编码信息，再加上其他模块恢复出这个图片的信息

主成分分析

目的

方法

将D维的原始数据X降维到M维的Z上，我们希望W是正交的，这样可以使得投影之后特征的冗余性尽可能的小

W的优化准则

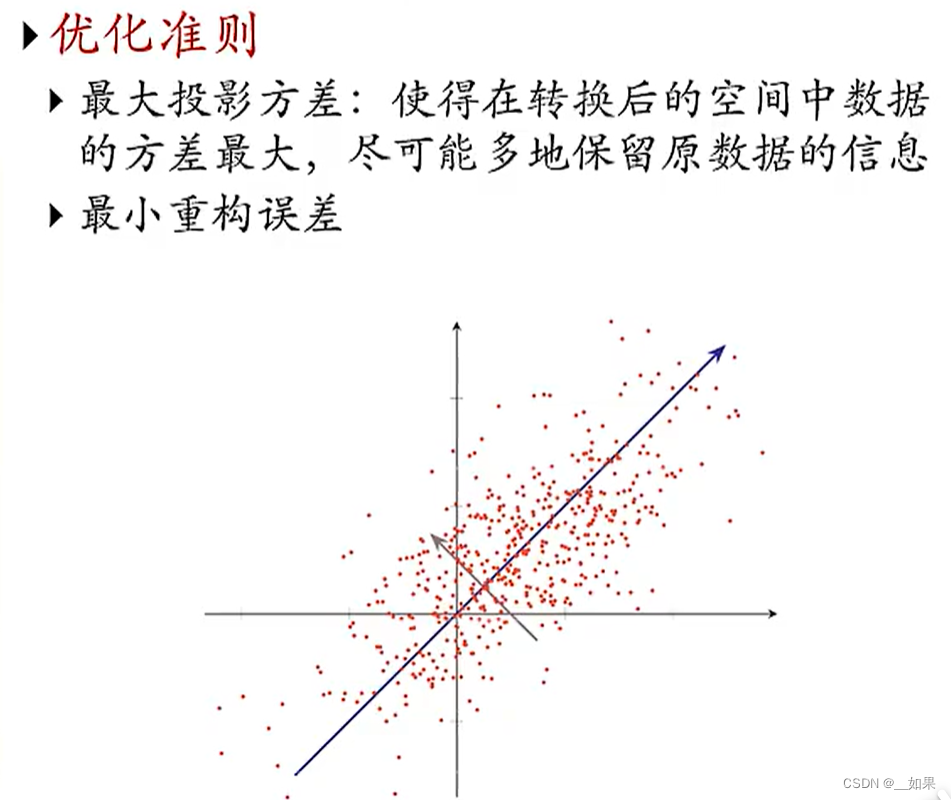
最大投影方差：在信息论中，方差越大，包含的信息越多

最小重构误差：X投影到Z又投影回X，误差最小

这两个优化目标的解是一样的，所以用PCA的时候直接用最大投影方差

具体优化

∑是原始空间中X的协方差矩阵

目标函数后面那项是约束项，w需要满足正交的条件

假设投影到一维：

左边同时乘w的转置，等号左边变成方差，右边变成λ(w正交相乘得1)

因此方差最大就变成了λ最大，由线代可知λ是∑协方差矩阵的特征值，于是便转化成求∑的最大特征值λ以及它对应的特征向量w

假设投影到多维：

求不同维度上的最大方差就是在求∑最大的几个特征值λ且满足λ对应的特征向量w皆正交

因此从D维投影到M维，其实就是求D维时的协方差矩阵∑的前M个最大的λ

编码与稀疏编码

(线性)编码

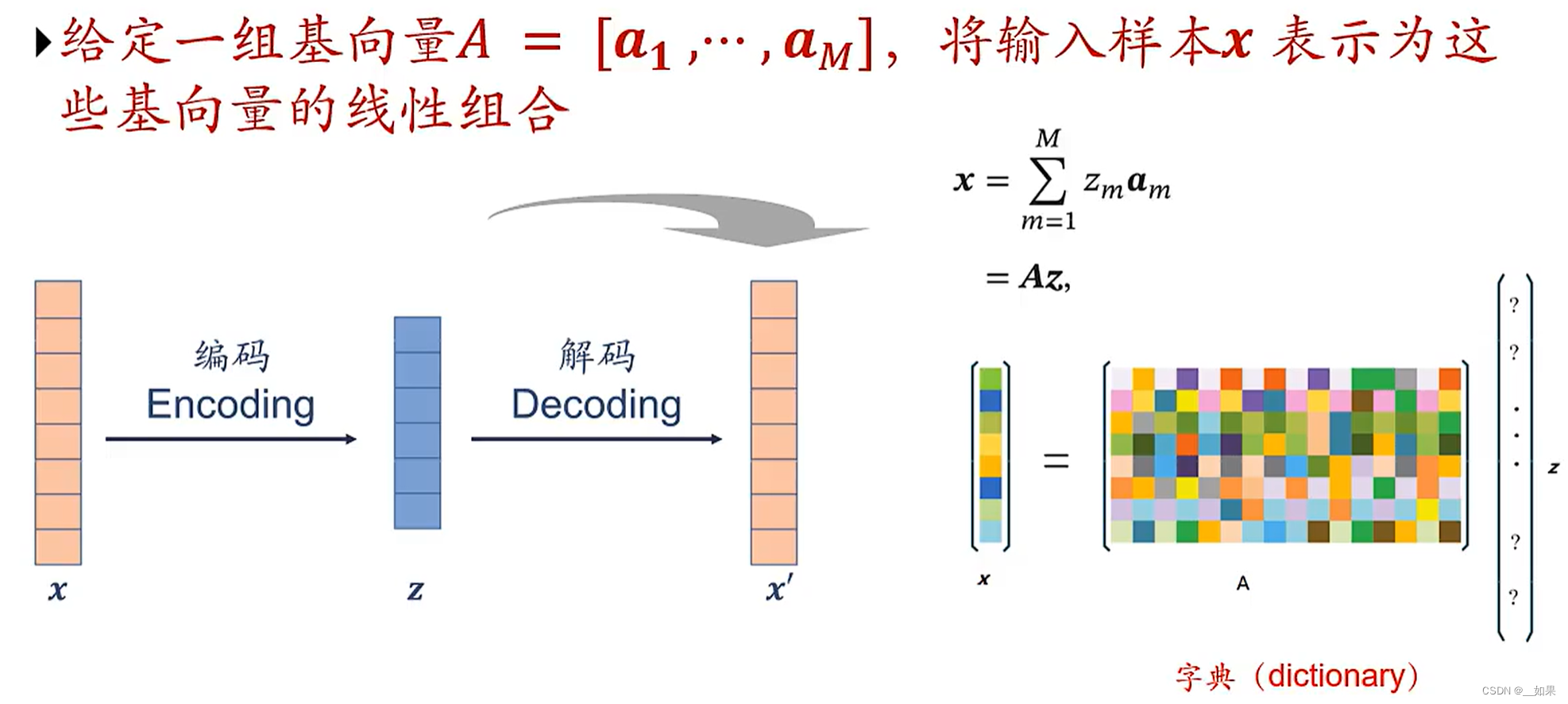
在无监督学习中，通常的一个特征学习流程是类似于这样一个编码解码的过程，先将x映射到一个隐藏的表示或隐藏的语义上，然后再通过解码映射到x的原始空间，z就是我们要学习的特征

假设编码解码都是线性的，那么这个z就可以通过一个线性的，比如矩阵，z=Wx得到，PCA也是类似的思想

我们能不能直接把每个样本对应的编码z和对应的权重w学到，而不用经过encoding呢？

当然是可以的。字典A的每一列都是基向量，x就是这些基向量的线性组合，z是编码向量

A与z是需要我们去学习的，要使Az得到的x与原始特征x尽可能的接近。固定A学习z，固定z学习A，注意这里的A是在所有样本上共享学习的

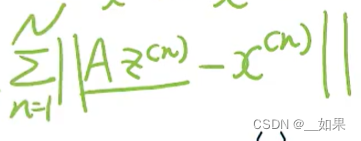最小化这个式子就是我们的学习与优化目标

稀疏编码

当z的维度大于x时称为过完备，存在冗余的特征；z的维度小于x的维度称为欠完备，若数据的特征不存在冗余性的话，z是不足以重构出x的

过完备本身有很多种解释并且一定存在这种现象，通常来说没有什么意义，但是如果我们赋予它一个属性——稀疏性，它就变得有意义了

当z十分稀疏时，如右图，假设一张图片它是D维的，基向量是M维的，且M大于D，这时由于z十分稀疏，导致基向量只在3个维度上有值，其余维度全为0。这样相当于每个原始空间中的特征都可以由少数基向量加权构成

稀疏编码的意义在于，人脑中的编码也是具有稀疏性的，神经元的激活是稀疏的，我们用少量的神经元就可以表示一个非常高维的特征，所以我们认为稀疏编码是具有某种生物学特性的

具体做法

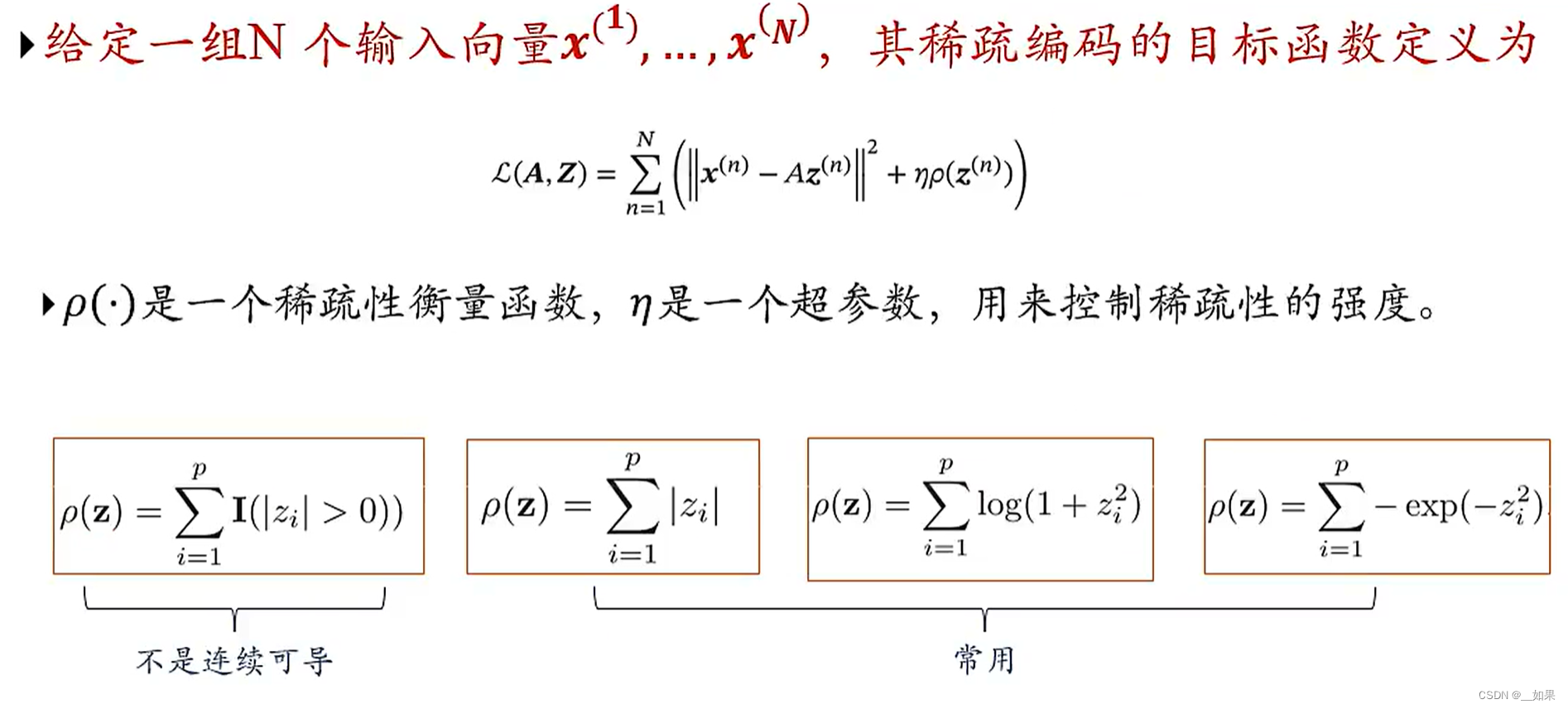
目标函数的前一个式子是重构误差，后一个式子是控制z的稀疏性

衡量稀疏性最直接的方法就是看0有多少个，也就是左下角的函数，但是它的数学性质不好，所以我们通常用后面三种间接的、近似的稀疏性衡量函数去代替

优点

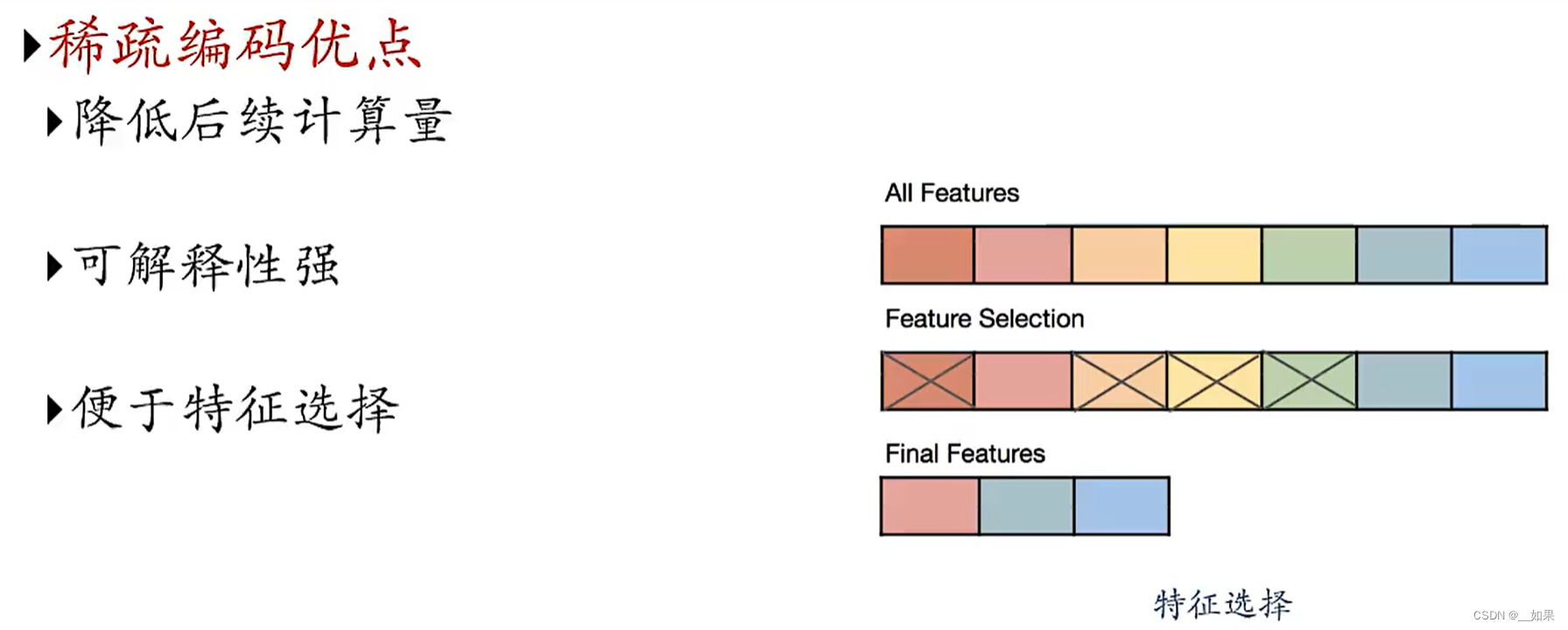
可解释性：我们很容易知道x主要是依赖于哪几个基向量

自编码器

x->z->x'整个流程都要学一遍

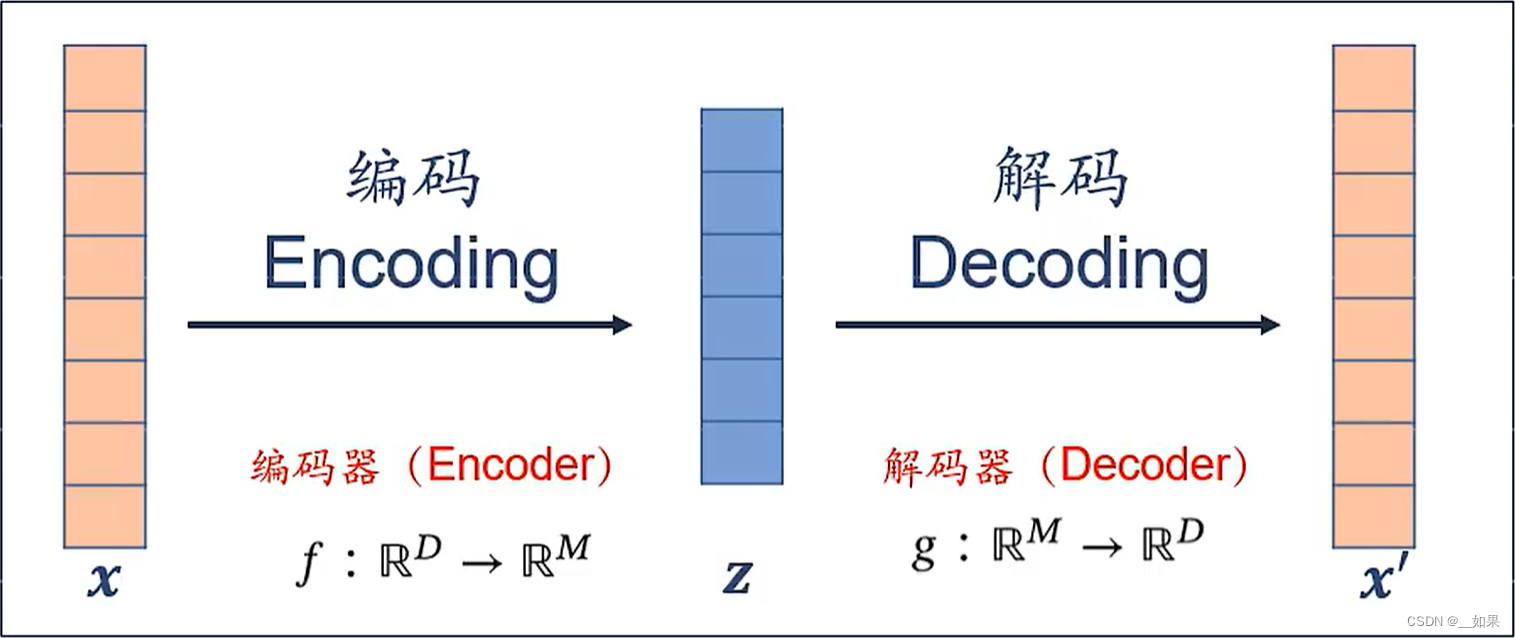
编码器f和解码器g是非线性的，如果f是线性且正交的就变成了PCA

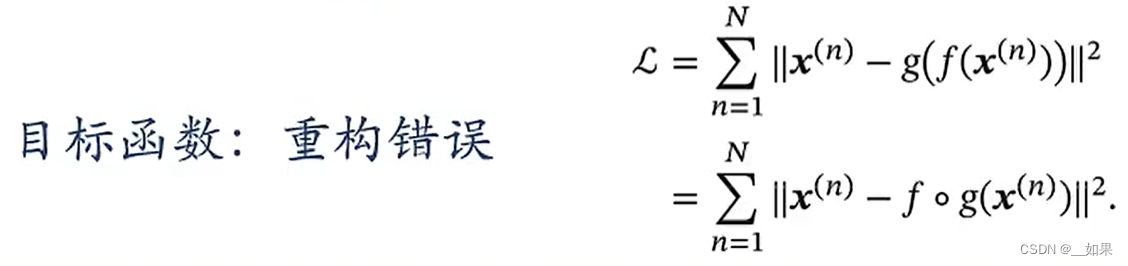
通过重构错误来学习f与g

两层网络为例

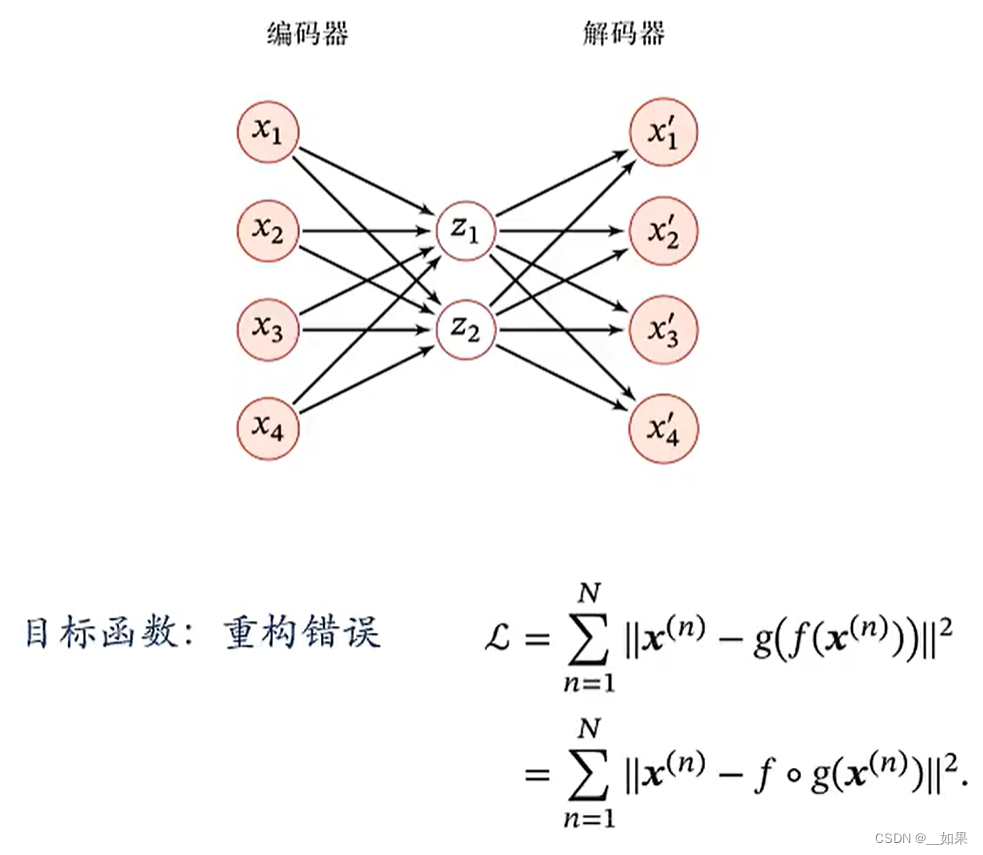
中间的隐藏层可以看作z

最终需要编码时只需要用前半部分x->z就行了

由于编码过程与解码过程是对称的，x->z的w与z->x'的w’肯定不一样，但在学习上我们可以使他们两个是转置的关系，这样学习起来会更容易

稀疏自编码器

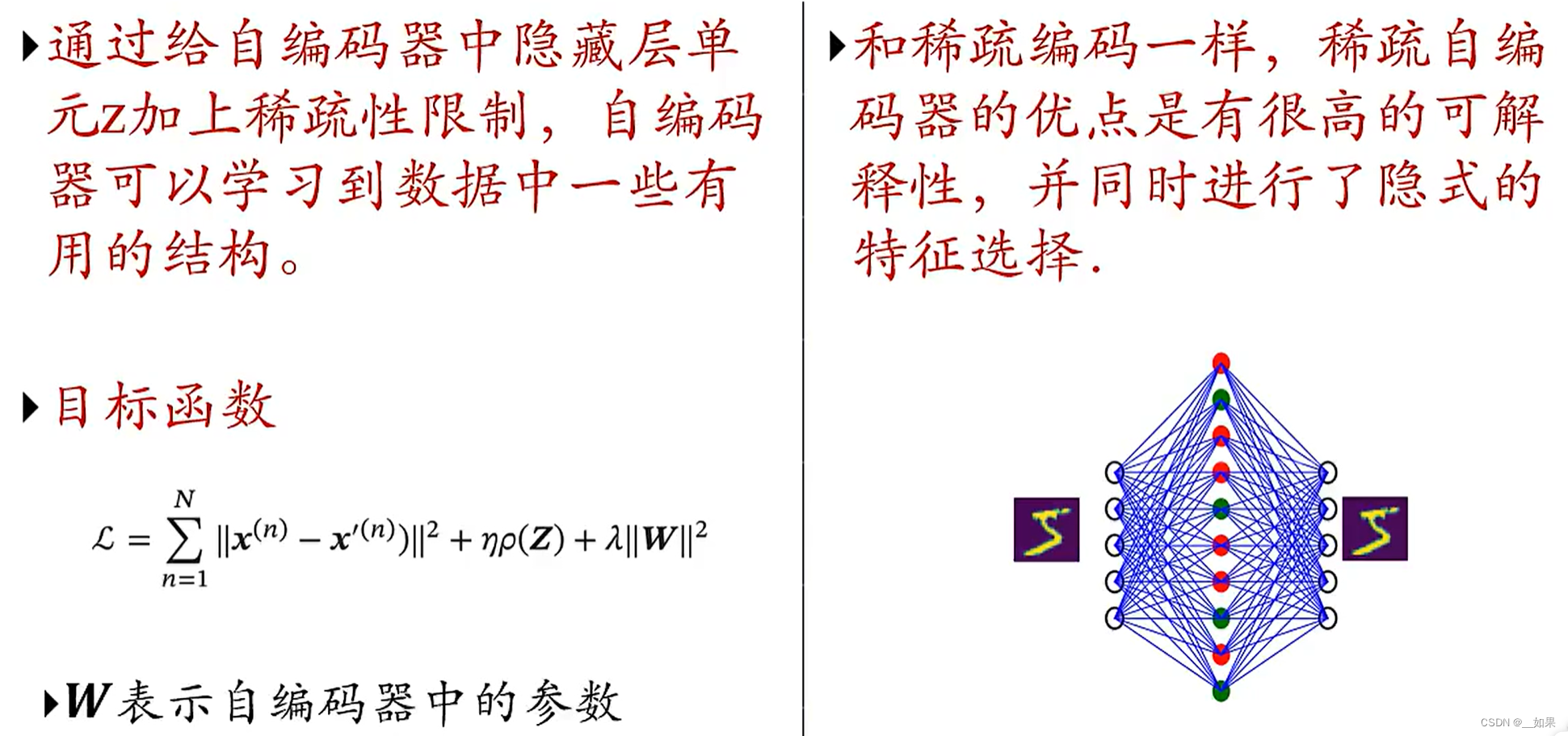
降噪自编码器

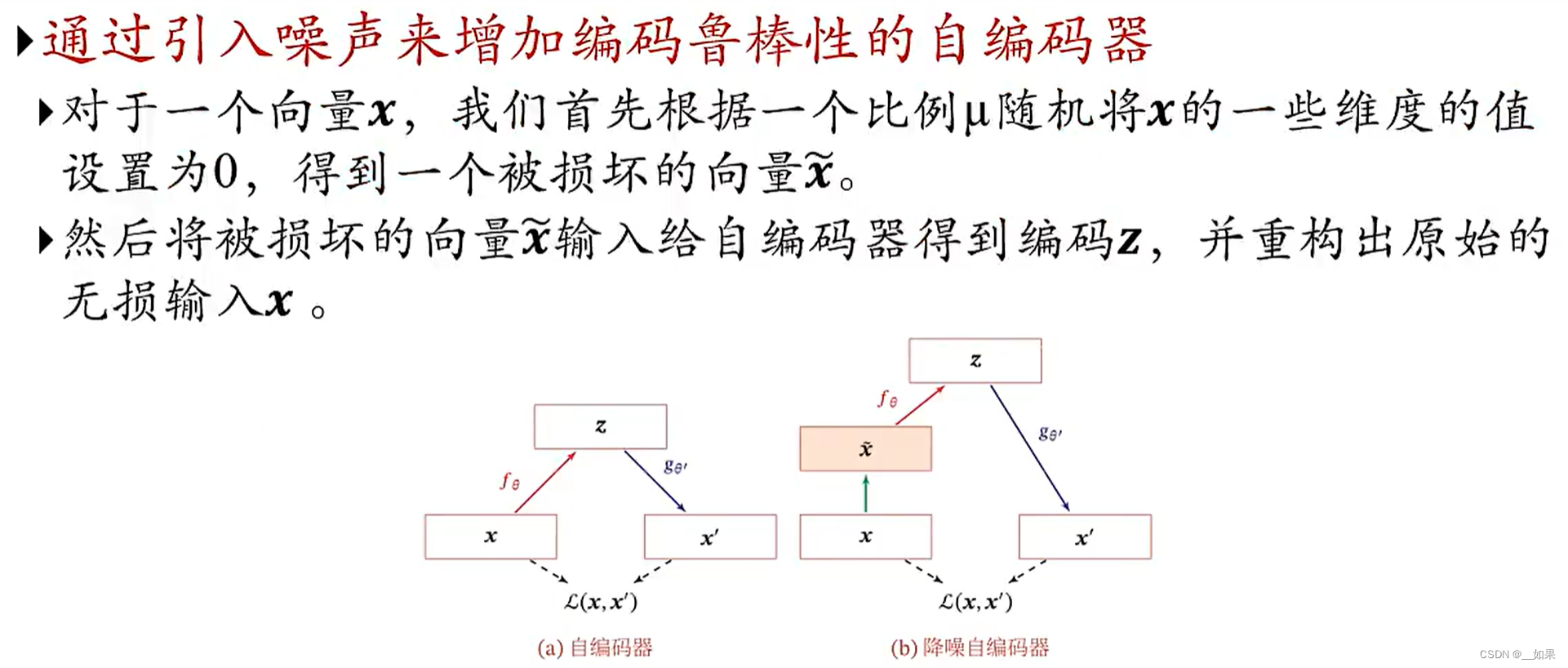
目标函数

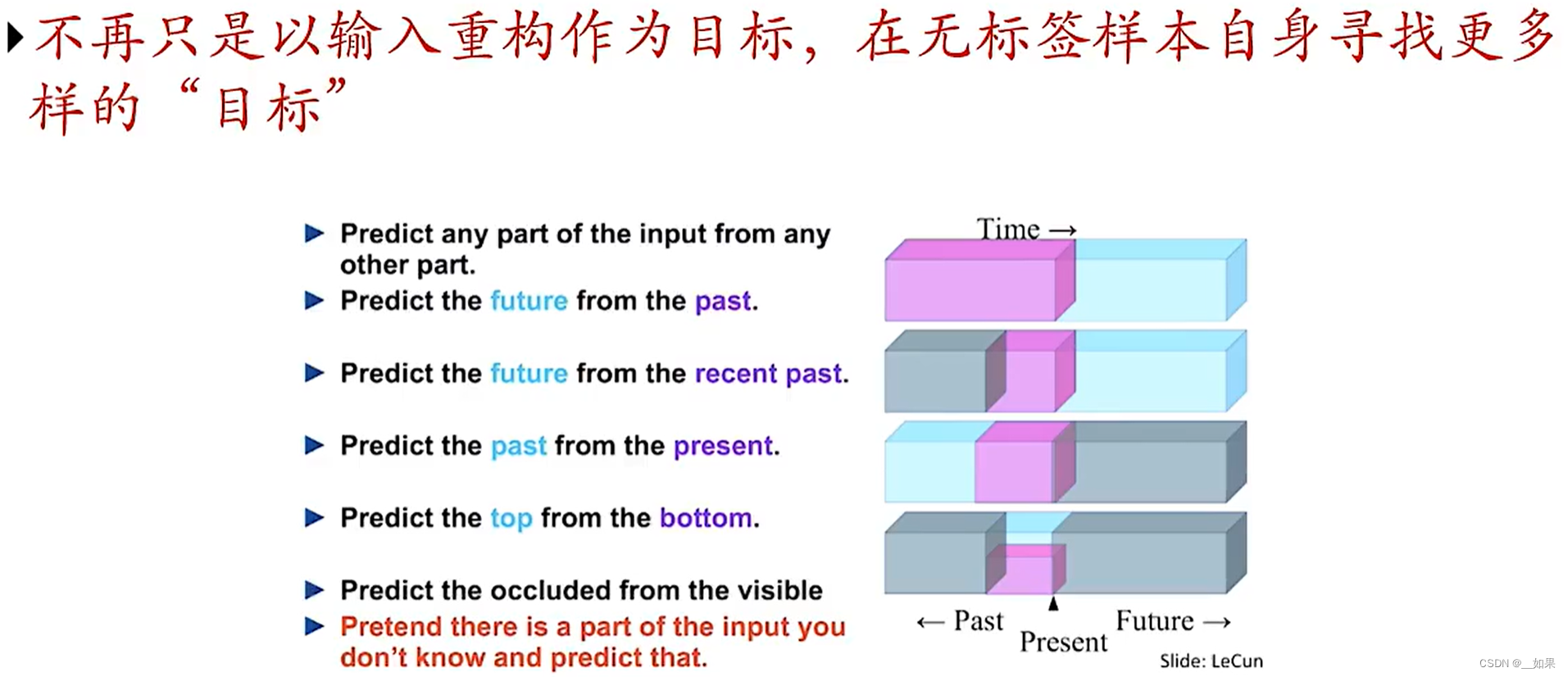
之前所用的目标函数都是重构错误，但自编码的目标可以很灵活

通过一张图片的一部分预测另一部分、通过过去预测未来、通过底端预测顶端等等

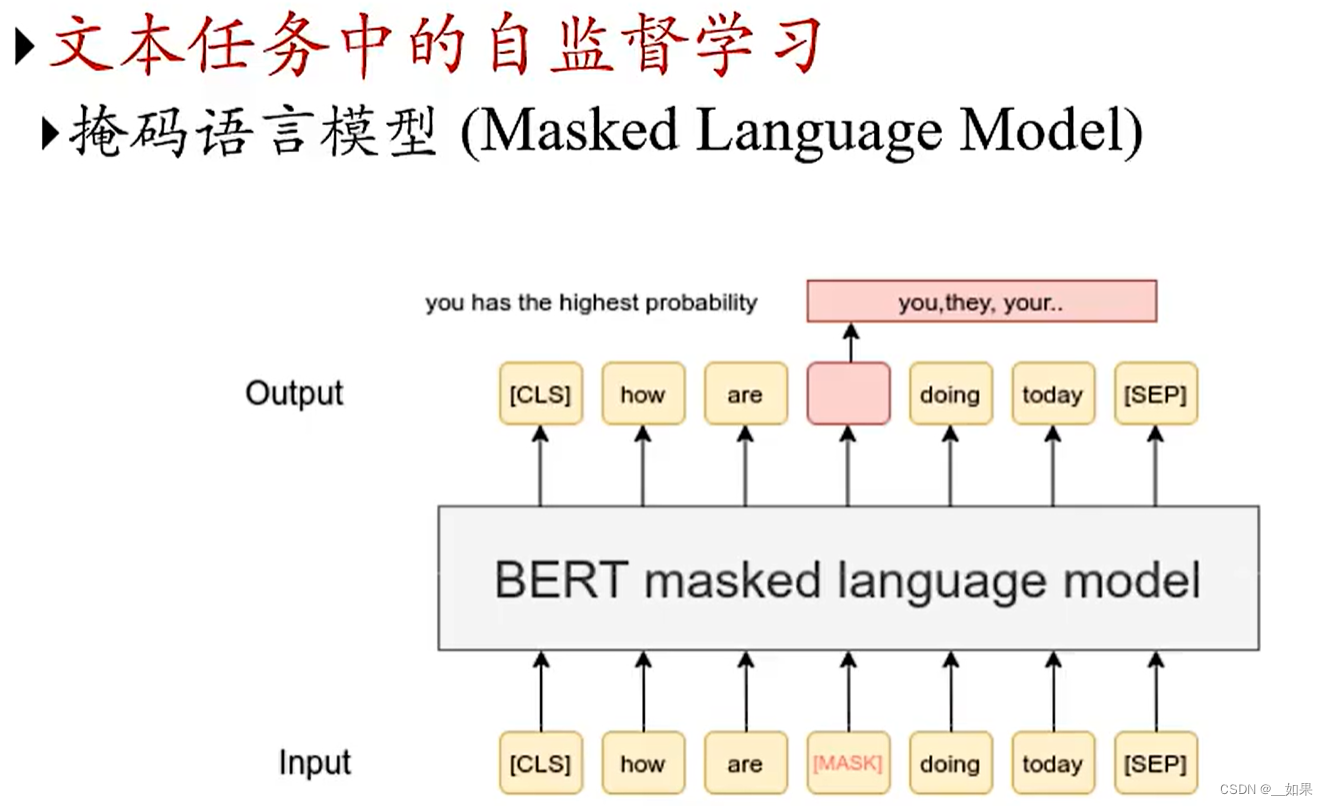
自监督学习

自监督学习与无监督学习的区别在于：自监督学习仍然是一个x->y的映射学习，这里的y是人为构造出的

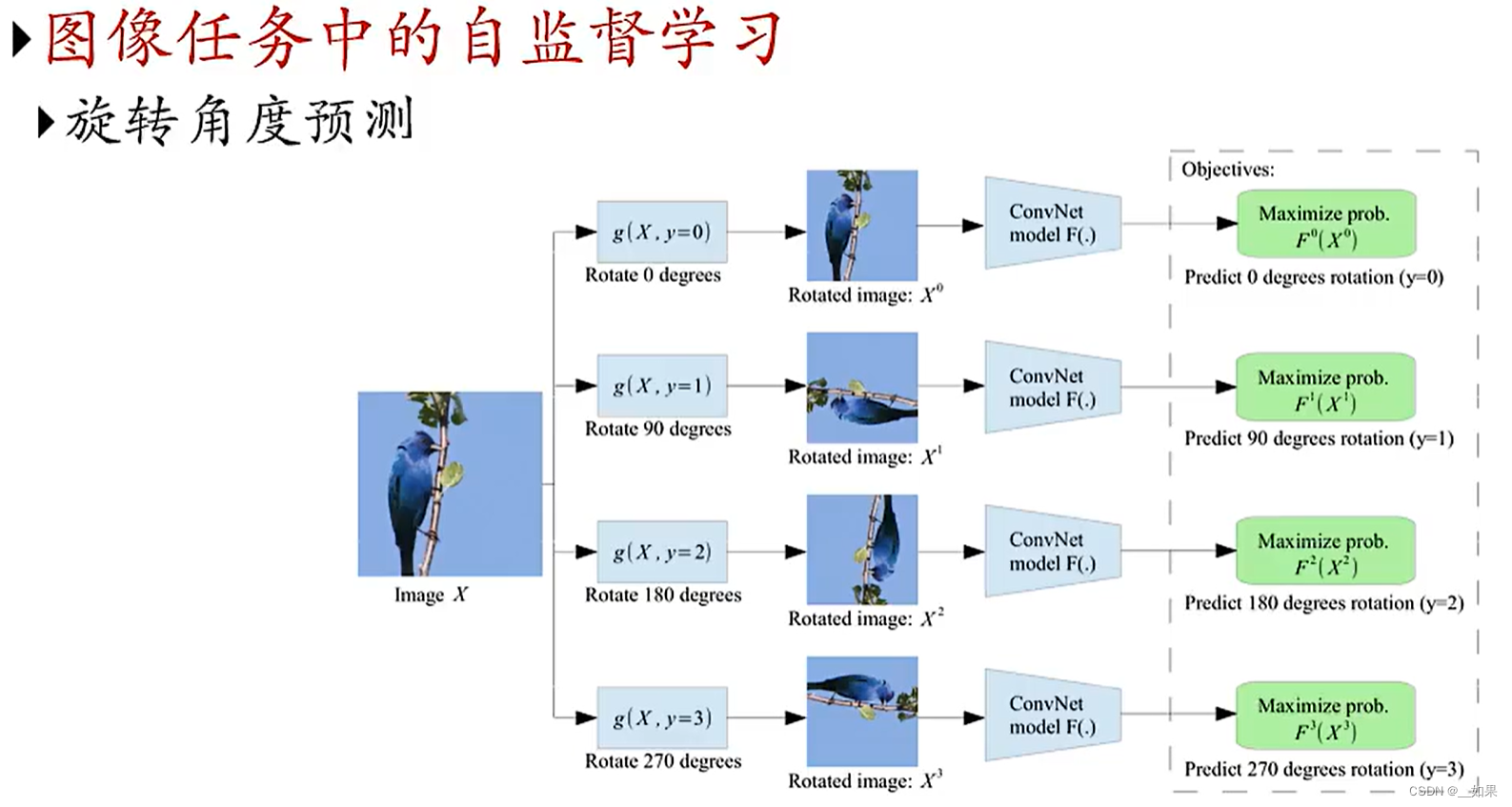
例如我们将图片做不同角度的旋转，然后再通过一个编码器，将它映射到一个y上，y就对应了图片的旋转角度

也就是说，我们人为的对x进行扰动且只利用x本身，可以产生一些额外的信息，在很多的任务上证明这种通过人为构造伪任务来进行的自监督学习，也能学习到一种非常好的x的表示

概率密度估计

典型的概率密度估计有两种：

参数密度估计

连续常用：

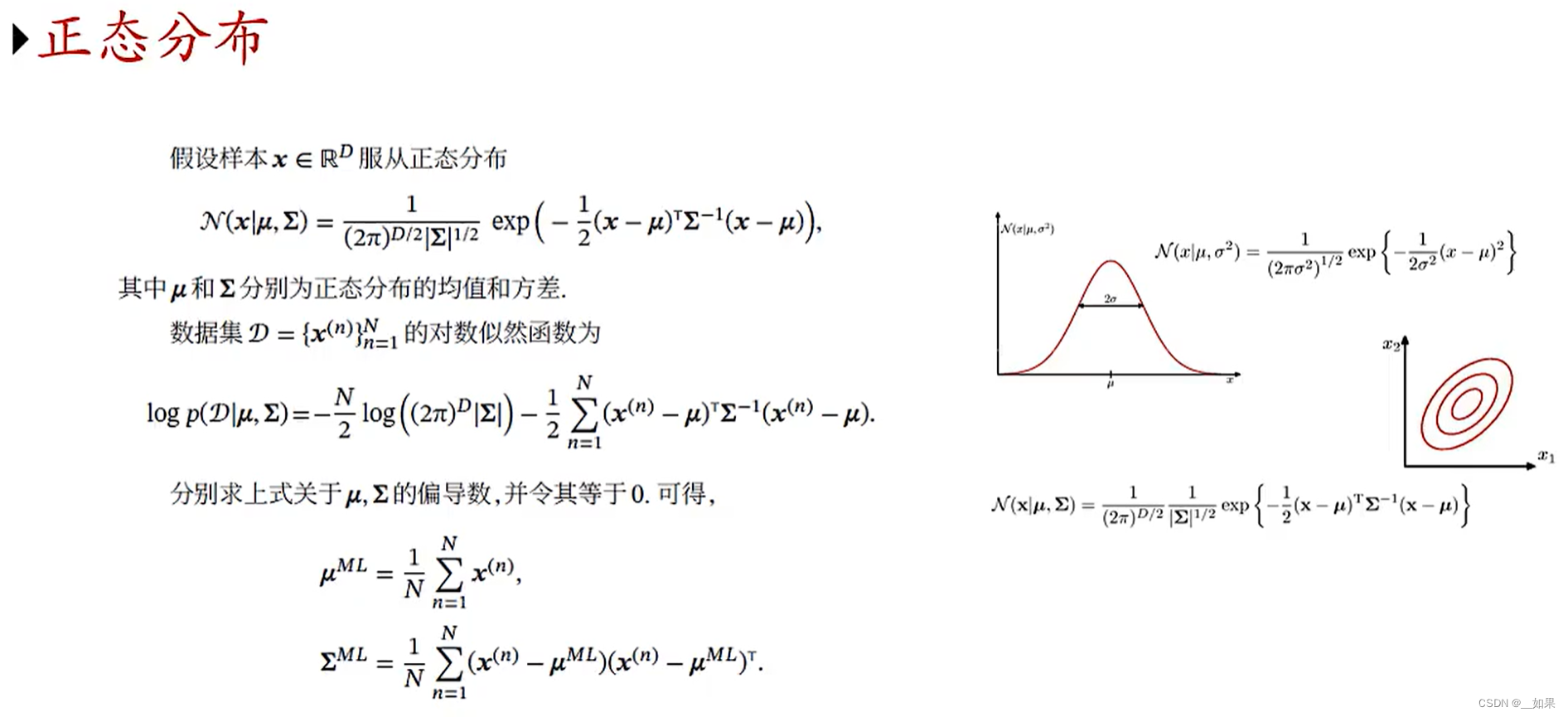
离散常用：

存在的问题

不可观测变量问题：比如x的分布依赖于某个变量z，但是我们只有x的数据

非参密度估计

直方图方法

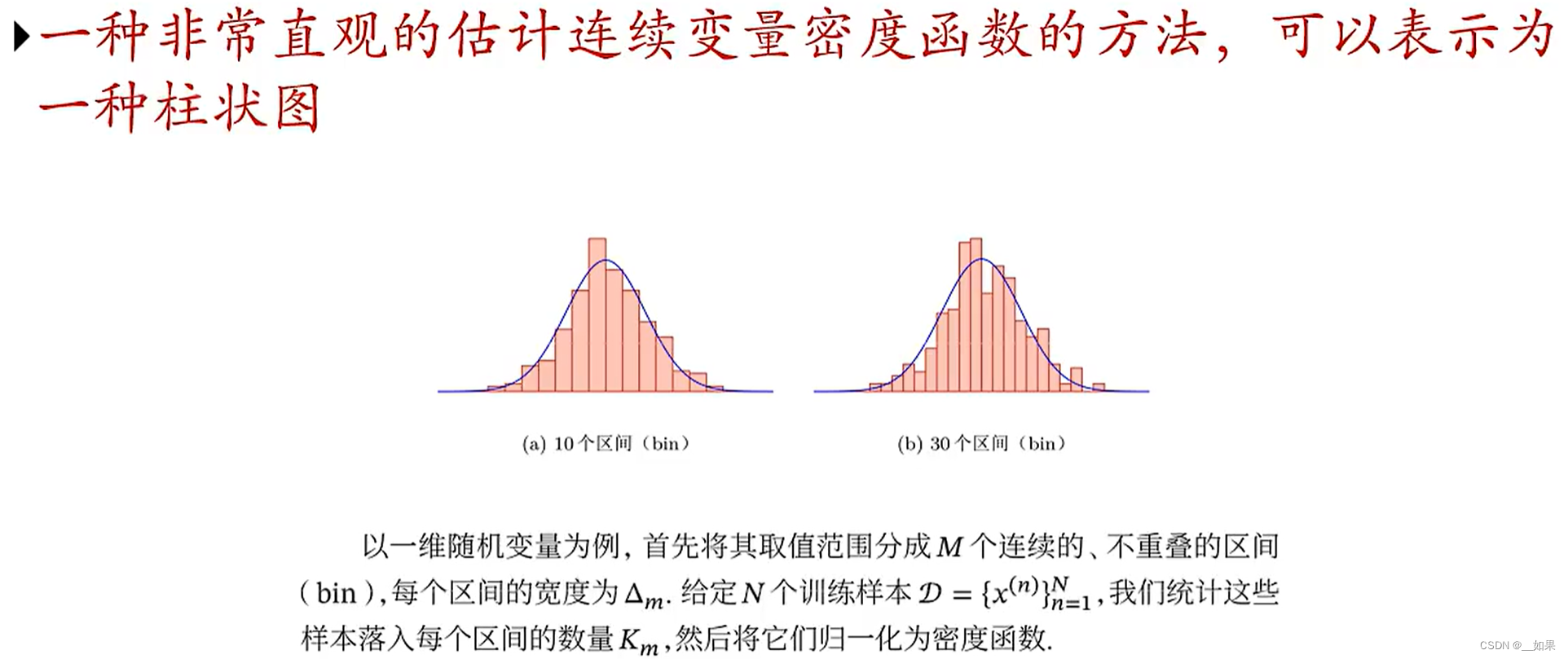
（1）M取的小，落入区间的个数越多，曲线越平滑，不会出现空的区间，但是精读不够；M大则反之

（2）由于对区间的划分是提前设置好的，对于临界点，可能会出现左边密度远远高于右边的密度，这使得直方图估计连续变量时估的不太精确

核密度估计

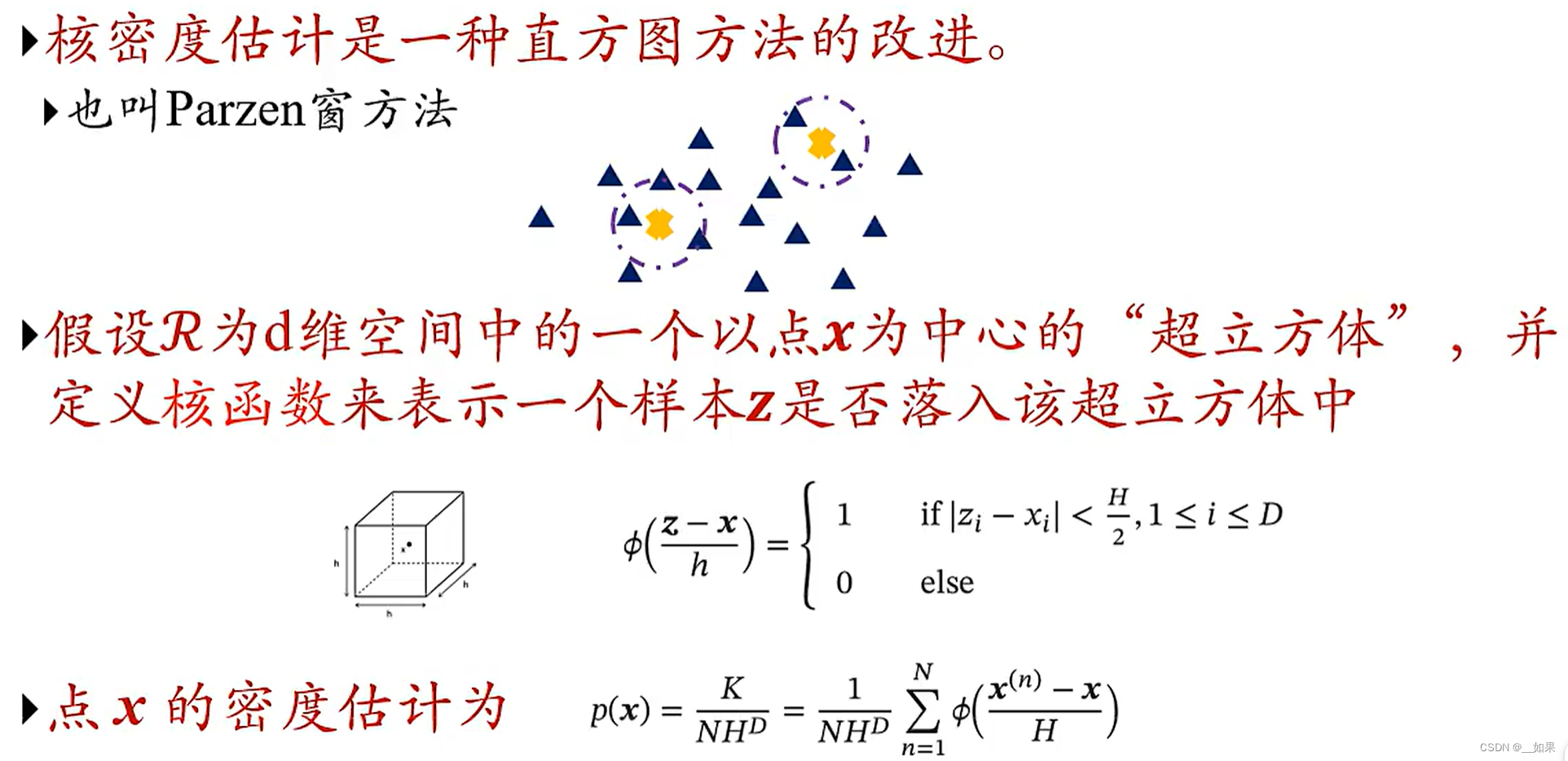
K就是落入x为中心的核函数的∑

V是固定的，是自己设置的超立方体的体积，只有K是变化的

K近邻方法

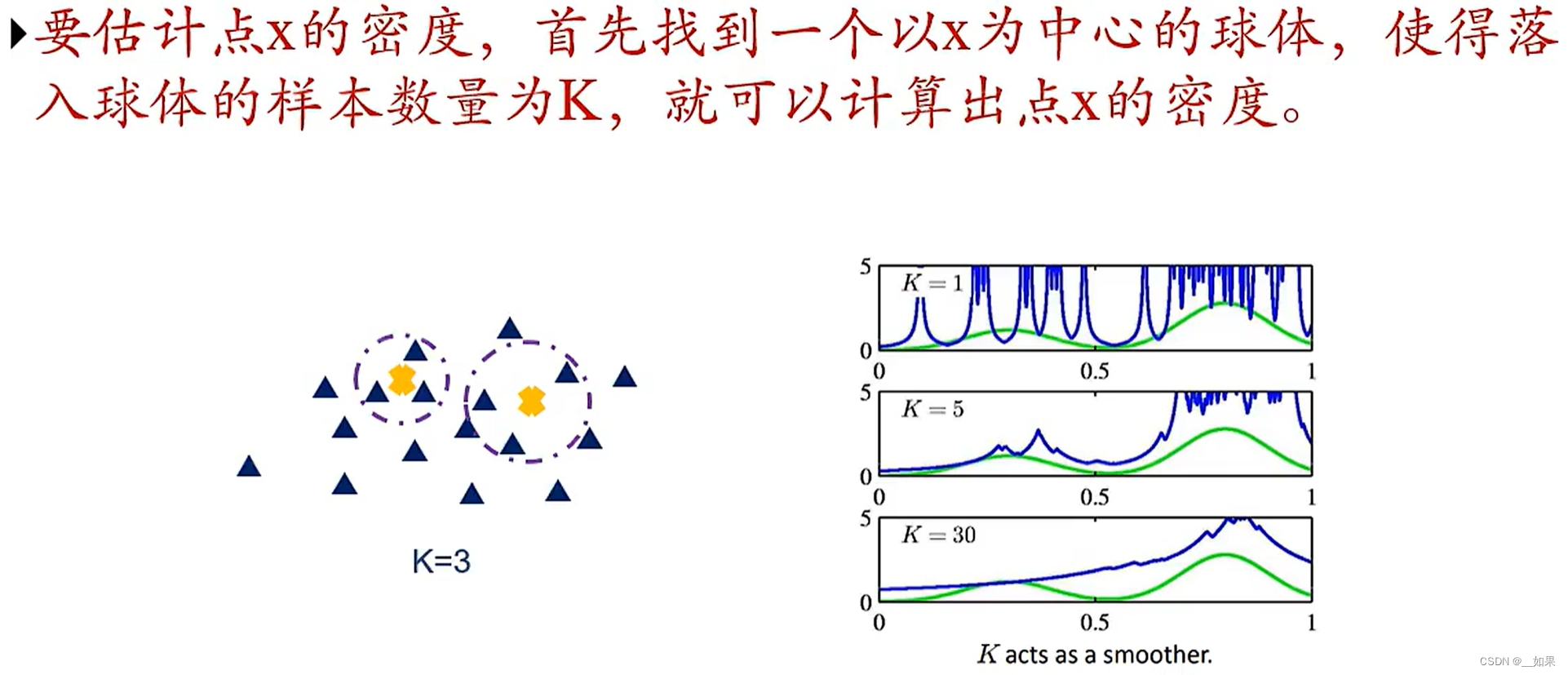
与核密度相反，K近邻是K固定，V变化

K太小不稳定，如果刚好有点小范围凑一起，密度函数会很大，通常K需要的取大一点

缺点

参数密度估计是基于对数据分布进行假设，通常假设数据服从某种特定的概率分布（比如正态分布、指数分布等）。在参数密度估计中，我们试图通过寻找最适合数据的参数，来拟合整个数据集的分布。一旦确定了参数，整个数据集对于密度估计来说就变得不再必要，因为我们已经用参数化的分布模型对整个数据的分布特征进行了建模。

相比之下，非参数密度估计不对数据分布作出明确的假设，它是一种更加灵活的估计方法，可以更好地适应数据的特征。通常采用的方法包括核密度估计和最近邻方法。这些方法通常需要在整个数据集上进行运算，因为它们不做任何对数据分布的假设，而是直接基于数据的排列情况来进行密度估计。因此，需要保留整个数据集作为输入，以便进行这些非参数方法的计算。

思考

估计p(y|x)就是判别式模型，并不需要对数据建模

估计p(xy)就是生成式模型，p(xy)=p(y)p(x|y)，通常来讲y是离散的标签，所以p(y)一般是一个多项分布的参数估计问题；而x通常是连续的，给定y，我们可以把x归到不同的类中，每个类去估计自己的类密度函数

我们的目的是pθ逼近pr，可以用KL散度去计算这俩分布的差异，最小化KL相当于最大化似然

半监督学习

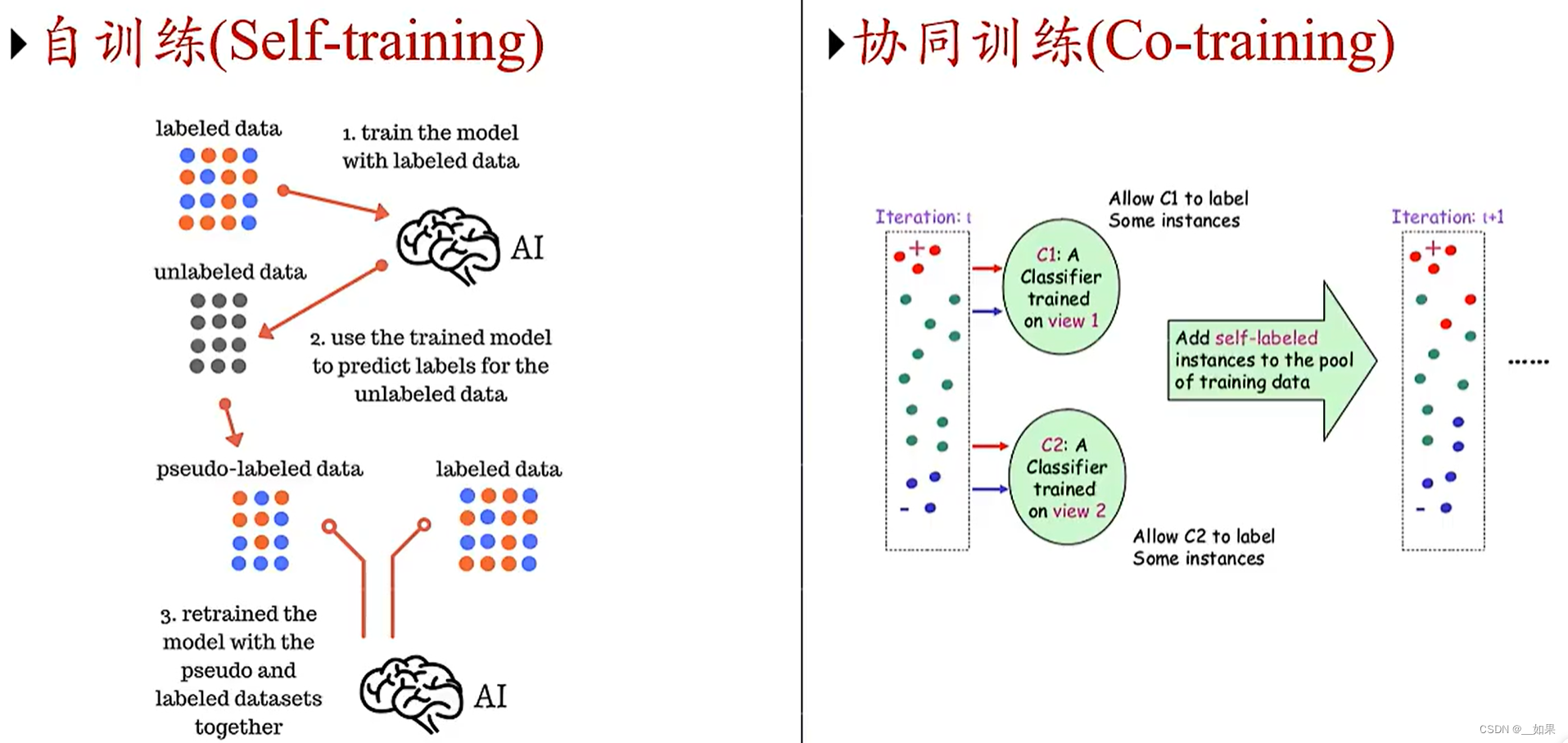
自训练

我们有一部分有标签数据和大量无标签数据，先用有标签数据训练一个模型，然后把这个模型用到无标签数据上让它分类，这样就得到了很多伪标签数据，再通过一些准则来筛选一些确定性比较高的数据，与有标签数据放一起作为新的数据集，不断训练迭代

协同训练

两个分类器分别使用原始数据的不同特征训练，如果这两个特征之间具有互补性，则可以互相提供对对方训练有利的样本