线性回归+小批量梯度下降算法

1.线性模型计算预测值：

• 线性模型可以看做单层神经网络。
  
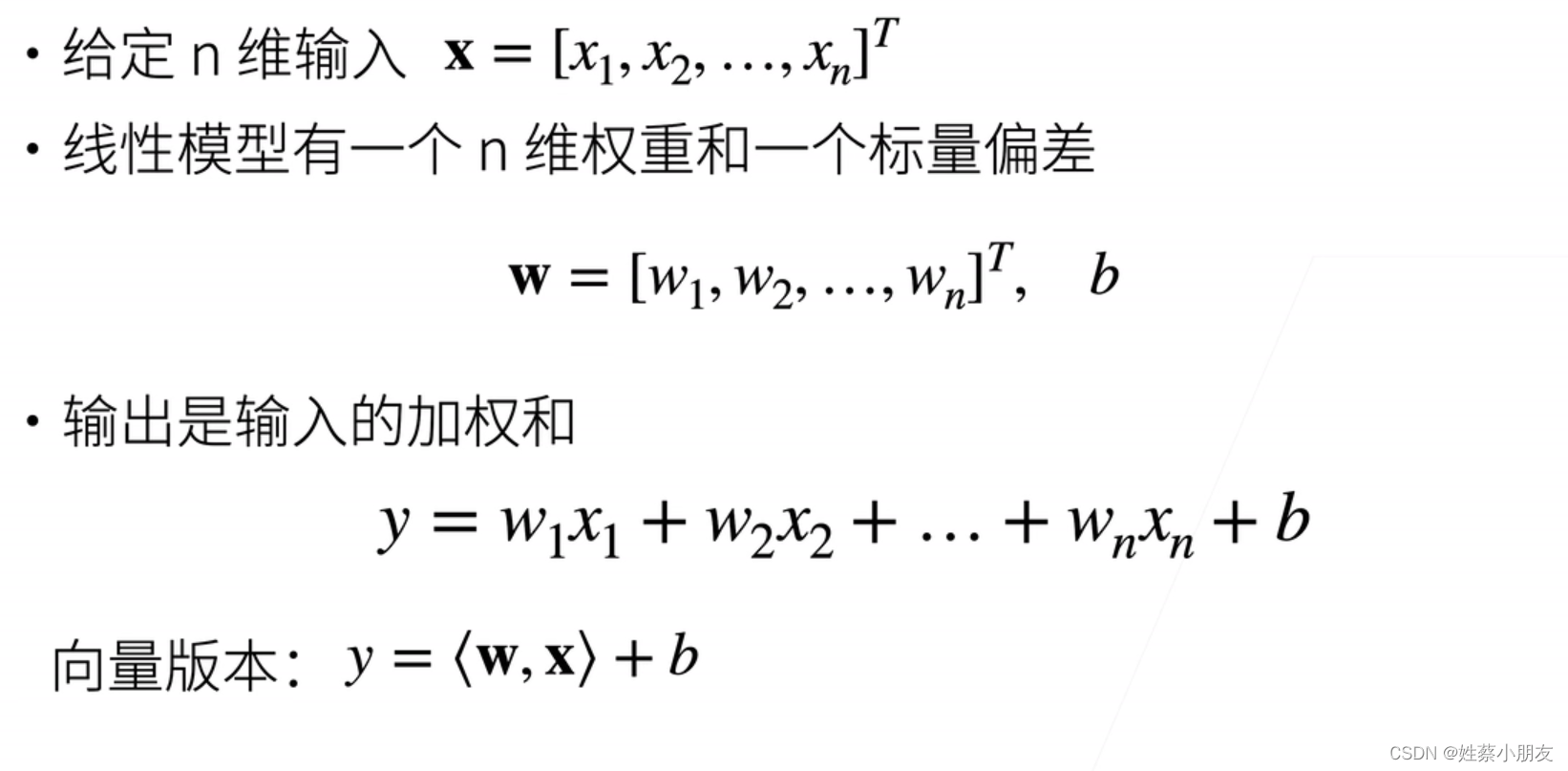
• 使用线性模型可以对每个样本数据x计算其预测值y
  • x为一个样本数据一维向量
  • w为权重一维向量，值表示x对应位置所占的权重，未知
  • b为偏差值，未知
  • y为预测值，即加权平均值

2.使用均方损失作为损失函数：

• 平方损失函数可以计算每个样本真实值和预测值之间的差值L
  • y为预测值
  • y^为真实值
  • L为平方差值

3.基础优化算法：梯度下降

• 每个圈是一个固定函数值，其中w0为初始函数值
• 黄线方向是负梯度：函数值沿负梯度方向下降最快
• 学习率η：沿某个方向走多远距离，太大太小都影响准确率
• 负梯度×η即沿负梯度方向走η距离
• 接下来的时刻不断更新wt使其不断接近最优解，即带入平方损失函数后L最小

4.训练数据：

• x为每个样本数据，为一维向量
• y为真实值，为数

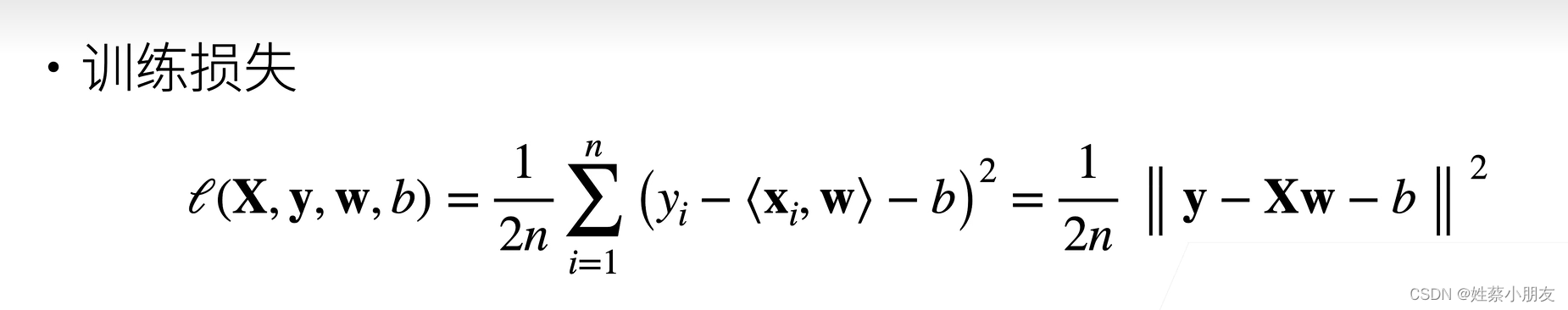
• 训练数据的目的是根据优化算法不断更新w、b，根据平方损失函数与真实值y和预测值y^不断计算L，得到的使得L最小的w、b即为w*、b*。
• 1/2来自损失函数
• 1/n求均值
• 对每个样本真实值y减每个样本预测值y^与偏差值b

5.线性回归实现：

%matplotlib inline
import random
import torch
from d2l import torch as d2l

#函数功能：根据“y=Xw+b+噪声”这个线性模型生成一个人造数据集
def synthetic_data(w, b, num_examples): 
    #X是均值为0，方差为1的大小为(num_examples, len(w))的向量
    X = torch.normal(0, 1, (num_examples, len(w)))
    #y=Xw+b+噪声
    y = torch.matmul(X, w) + b
    y += torch.normal(0, 0.01, y.shape)
    return X, y.reshape((-1, 1))
#真实值w
true_w = torch.tensor([2, -3.4])
#真实值b
true_b = 4.2
#根据函数计算特征矩阵和标签向量
features, labels = synthetic_data(true_w, true_b, 1000)

#函数功能：特征矩阵、标签向量作为输入，生成多个大小为batch_size大小的小批量batch_indices
def data_iter(batch_size, features, labels):
    num_examples = len(features)
    
    indices = list(range(num_examples))
    # 打乱样本顺序，保证随机存取
    random.shuffle(indices)
    #每次循环从i----i+batch_size的下标中获取batch_size个样本，赋值给batch_indices作为一个小批量
    for i in range(0, num_examples, batch_size):
        batch_indices = torch.tensor(
            indices[i: min(i + batch_size, num_examples)])
        #对每个小批量batch_indices计算其特征矩阵、标签向量
        yield features[batch_indices], labels[batch_indices]

#定义初始化模型参数        
w = torch.normal(0, 0.01, size=(2,1), requires_grad=True)
b = torch.zeros(1, requires_grad=True)  
#定义模型
def linreg(X, w, b):  
    """线性回归模型"""
    return torch.matmul(X, w) + b

#定义损失函数
def squared_loss(y_hat, y): 
    """均方损失"""
    return (y_hat - y.reshape(y_hat.shape)) ** 2 / 2

#定义优化算法：在每一步中，使用从数据集中随机抽取的一个小批量，然后根据参数计算损失的梯度
def sgd(params, lr, batch_size):  
    """小批量随机梯度下降"""
    with torch.no_grad():
        for param in params:
            param -= lr * param.grad / batch_size
            param.grad.zero_()

#训练过程
lr = 0.03#lr是学习率
num_epochs = 3#num_epochs是训练过程的迭代次数
net = linreg
loss = squared_loss

for epoch in range(num_epochs):
    for X, y in data_iter(batch_size, features, labels):
        l = loss(net(X, w, b), y)  # X和y的小批量损失
        l.sum().backward() # l中的所有元素被加到一起，并以此函数计算关于[w,b]的梯度
        sgd([w, b], lr, batch_size)  # 使用参数w、b的梯度更新参数w、b
    with torch.no_grad():
        train_l = loss(net(features, w, b), labels)
        #输出损失值
        print(f'epoch {epoch + 1}, loss {float(train_l.mean()):f}')

6.线性回归总结：

• 1.给定n个一维向量x和n个数y^作为训练数据
• 2.使用小批量梯度下降算法不断更新w、b的值
• 3.对于当前w、b，不断使用线性模型计算预测值y
• 4.对于当前y，不断使用平方损失函数计算损失L
• 5.输出最小L，此时w、b即为w*、b*

注：初学者个人理解，如有问题，感谢指正。