LeetCode 142. 环形链表 II
发布时间:2023年12月18日
给定一个链表的头节点 ?head?,返回链表开始入环的第一个节点。?如果链表无环,则返回?null。
如果链表中有某个节点,可以通过连续跟踪?next?指针再次到达,则链表中存在环。 为了表示给定链表中的环,评测系统内部使用整数?pos?来表示链表尾连接到链表中的位置(索引从 0 开始)。如果?pos?是?-1,则在该链表中没有环。注意:pos?不作为参数进行传递,仅仅是为了标识链表的实际情况。
不允许修改?链表。
示例 1:

输入:head = [3,2,0,-4], pos = 1
输出:返回索引为 1 的链表节点
解释:链表中有一个环,其尾部连接到第二个节点。
示例 2:

输入:head = [1,2], pos = 0
输出:返回索引为 0 的链表节点
解释:链表中有一个环,其尾部连接到第一个节点。
示例 3:

输入:head = [1], pos = -1
输出:返回 null
解释:链表中没有环。
提示:
- 链表中节点的数目范围在范围 [0, 10^4] 内
- -10^5 <= Node.val <= 10^5
- pos 的值为 -1 或者链表中的一个有效索引
进阶:你是否可以使用 O(1) 空间解决此题?
解法思路:
1、hash,遍历每个节点并记录,再次遍历到则存在环并返回
2、快慢指针,先判断是否有环,若有,则找出环的第一个节点(从相遇点到入环点的距离加上 n?1 圈的环长,恰好等于从链表头部到入环点的距离,使用第三个指针(初始化指向head),third 与 slow 刚好在入环处相遇)
法一:
/**
* Definition for singly-linked list.
* class ListNode {
* int val;
* ListNode next;
* ListNode(int x) {
* val = x;
* next = null;
* }
* }
*/
public class Solution {
public ListNode detectCycle(ListNode head) {
// hash
// Time: O(n)
// Space: O(n)
ListNode pos = head;
Set<ListNode> set = new HashSet<>();
while (pos != null) {
if (set.contains(pos)) {
return pos;
} else {
set.add(pos);
}
pos = pos.next;
}
return null;
}
}?法二:
/**
* Definition for singly-linked list.
* class ListNode {
* int val;
* ListNode next;
* ListNode(int x) {
* val = x;
* next = null;
* }
* }
*/
public class Solution {
public ListNode detectCycle(ListNode head) {
// 快慢指针,先判断是否有环,若有,则找出环的第一个节点
// 1. 判断是否有环
if (head == null || head.next == null || head.next.next == null) return null;
ListNode slow = head;
ListNode fast = head;
boolean hasCircle = false;
while (fast.next != null && fast.next.next != null) {
slow = slow.next;
fast = fast.next.next;
if (slow == fast) {
hasCircle = true;
break;
}
}
// 2. 找出入环节点
// 从相遇点到入环点的距离加上 n?1 圈的环长,恰好等于从链表头部到入环点的距离
// 使用第三个指针(初始化指向head),third 与 slow 刚好在入环处相遇
if (hasCircle) {
ListNode third = head;
while (slow != third) {
slow = slow.next;
third = third.next;
}
return third;
}
return null;
}
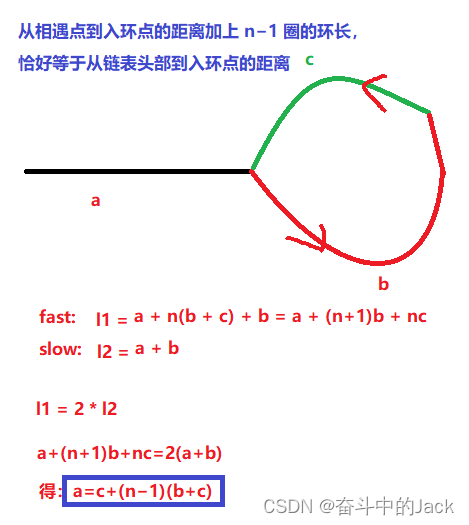
}数学证明:从相遇点到入环点的距离加上 n?1 圈的环长,恰好等于从链表头部到入环点的距离?
文章来源:https://blog.csdn.net/qq_38304915/article/details/135072068
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
最新文章
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- Mybatis&Mybatis-Plus
- YoloV8改进策略:将FasterNet与YoloV8深度融合,打造更快更强的检测网络
- JavaScript获取后端json数据创建表格
- Kotlin(十六) 高阶函数的简单应用
- Linux环境下HTTP请求的代码详解与实例
- Postman/Apifox使用教程
- IntelliJ IDE 插件开发 | (三)消息通知与事件监听
- 源码部署MySQL
- 3800个字彻底弄清cortex
- 程序员的海外营收