【数据结构——图】图的遍历(头歌习题)【合集】
目录
第1关:邻接矩阵存储图的深度优先遍历
任务描述
本关任务:请你实现 dfs.cpp 里的void DFS( MatGraph* G, VertexType V)函数。 约定:顶点编号小的先输出。
相关知识
为了完成本关任务,你需要掌握:1.如何使用邻接矩阵存储图,2.如何遍历图。
邻接矩阵存储图
一个包含6个顶点的无向图如图所示。
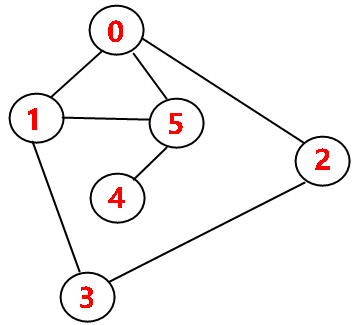
图1 一个包含6个顶点的无向图
图 2 给出了对图 1 的无向图的存储结构图:每个顶点的名称由一个整数描述,顶点的相邻关系保存在邻接矩阵中,矩阵中值为 1 表示i号顶点到j号顶点有边,为 0 表示无边。
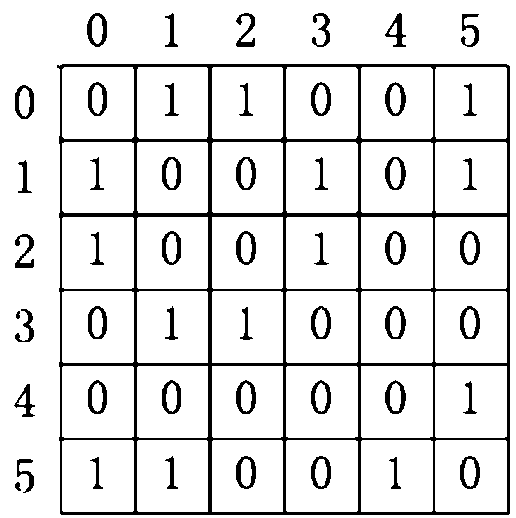
图2 图1的无向图的邻接矩阵
图的邻接矩阵定义如下:
typedef struct //图的定义
{
int edges[MAXV][MAXV]; //邻接矩阵
int n, e; //顶点数, 边数
VertexType vexs[MAXV]; //存放顶点信息
} MatGraph;
给定指向该结构的指针G,就可以对图进行操作。
图的遍历
所谓图的遍历(graph traversal),也称为搜索(search),就是从图中某个顶点出发,沿着一些边访遍图中所有的顶点,且使每个顶点仅被访问一次。遍历可以采取两种方法进行:深度优先搜索(DFS,depth first search)和广度优先搜索(BFS,breadth first search)。
深度优先遍历过程:
(1)从图中某个初始顶点v出发, 首先访问初始顶点v。
(2)选择一个与顶点v相邻且没被访问过的顶点w, 再从w出发进行深度优先搜索, 直到图中与当前顶点v邻接的所有顶点都被访问过为止。
算法设计思路:
深度优先遍历的过程体现出后进先出的特点:用栈或递归方式实现。

如何确定一个顶点是否访问过? 设置一个visited[] 全局数组, visited[i]=0表示顶点i没有访问; visited[i]=1表示顶点i已经访问过。
DFS伪代码——邻接矩阵存储实现
如果用邻接矩阵存储图(设顶点个数为 n),则 DFS 算法实现的伪代码如下:
DFS(图G, 顶点 i ) //从顶点 i 进行深度优先搜索
{
visited[ i ] = 1; //将顶点 i 的访问标志置为 1
for( j=0; j<n; j++ ) //对其他所有顶点 j
{
//j 是 i 的邻接顶点,且顶点 j 没有访问过
if( edges[i][j]==1 && !visited[j] )
{
//递归搜索前的准备工作需要在这里写代码
DFS( j ); //从顶点 j 出发进行 DFS 搜索
//以下是 DFS 的回退位置,在很多应用中需要在这里写代码
}
}
}
对图1运行该算法的结果(从顶点5出发): 5 0 1 3 2 4。
编程要求
请你在右侧的代码窗口中实现dfs.cpp里的void DFS( MatGraph* G, VertexType V)函数。 注意遵守约定:顶点编号小的先输出。
测试说明
本关的测试过程如下:
1.平台编译 step1/dfs.cpp ;
2.平台运行该可执行文件,并以标准输入方式提供测试输入;
3.平台获取该可执行文件的输出,然后将其与预期输出对比,如果一致则测试通过;否则测试失败。
输入输出格式说明:
输入格式:
输入V,开始遍历的起始顶点编号。
输出格式:
输出对图进行深度优先遍历的顶点序列,每个顶点编号前面有一个空格。
以下是平台对 step1/dfs.cpp 的测试样例:
样例输入:
无向图
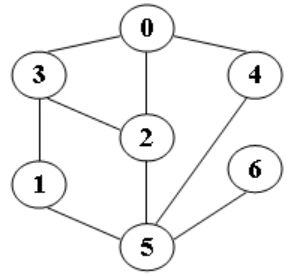
测试输入:5
样例输出:
预期输出:DFS from 5: 5 1 3 0 2 4 6
开始你的任务吧,祝你成功!
完整代码
#include "dfs.h"
/*
* 从顶点V出发进行深度优先搜索。
* 函数DFS应从编号为V的顶点出发递归地深度优先遍历图,
* 遍历访问邻接点时,要求按序号递增的顺序。
* 题目保证V是图中的合法顶点。
* 参数G为邻接矩阵存储的图的表示。
*/
void DFS( MatGraph* G, VertexType V)
{
/**
* 请在下面的begin..end间编写程序代码,
* 勿修改begin..end之外的代码。
*/
/*******************begin*******************/
int i=V; // 开始顶点
visited[i]=1;
printf(" %d", i);
int j;
for(j=0; j<G->n; j++){
if(G->edges[i][j]==1 && !visited[j]){
DFS(G, j);
}
}
/*******************end********************/
}
int main()
{
MatGraph* G;
VertexType V;
G = CreateGraph();
scanf("%d", &V);
printf("DFS from %d:", V);
DFS(G, V);
return 0;
}
第2关:邻接表存储图的广度优先遍历
任务描述
本关任务:请你实现 bfs.cpp 里的void BFS( AdjGraph* G, VertexType V)函数。 约定:顶点编号小的先输出。
相关知识
为了完成本关任务,你需要掌握:1.如何使用邻接表存储图,2.如何遍历图。
邻接表存储图
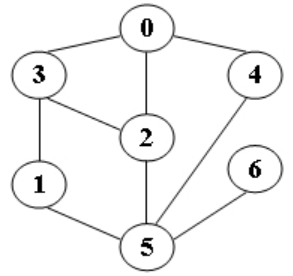
一个包含5个顶点的无向图如图所示。
一个包含5个顶点的无向图
图1 一个包含5个顶点的无向图
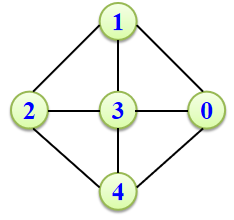
图 2 给出了对图 1 的无向图的邻接表存储结构图:每个顶点的名称由一个整数描述,对图中每个顶点i建立一个单链表, 将顶点i的所有邻接点链起来。
每个顶点的邻接表
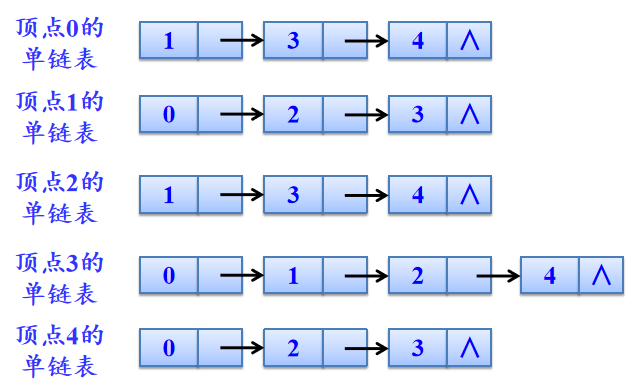
每个单链表上添加一个表头结点(表示顶点信息)。并将所有表头结点构成一个数组, 下标为i的元素表示顶点i的表头结点。
邻接表
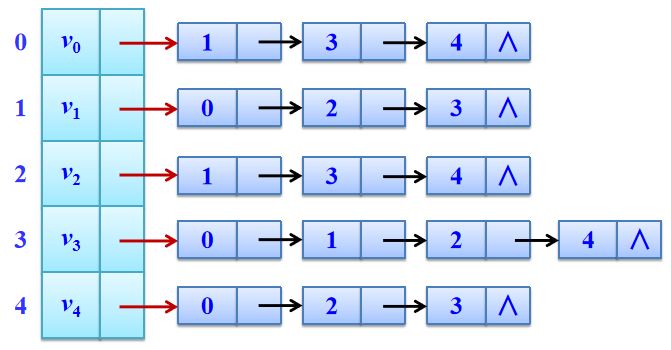
图2 图1的无向图的邻接表
图的邻接表存储方法是一种顺序分配与链式分配相结合的存储方法,如图3所示。
图的邻接表
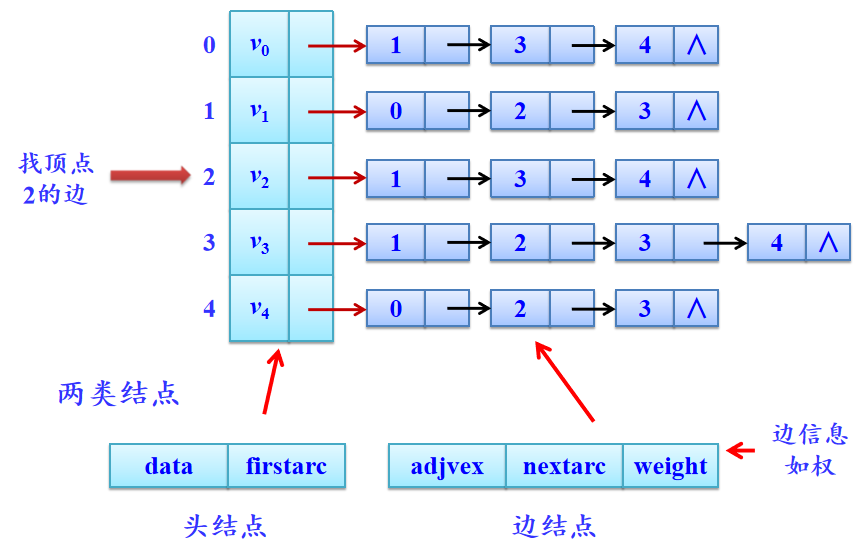
图3 图的邻接表表示形式
一个带权的有向图(网)的邻接表存储形式如图4所示。
带权有向图的邻接表存储形式
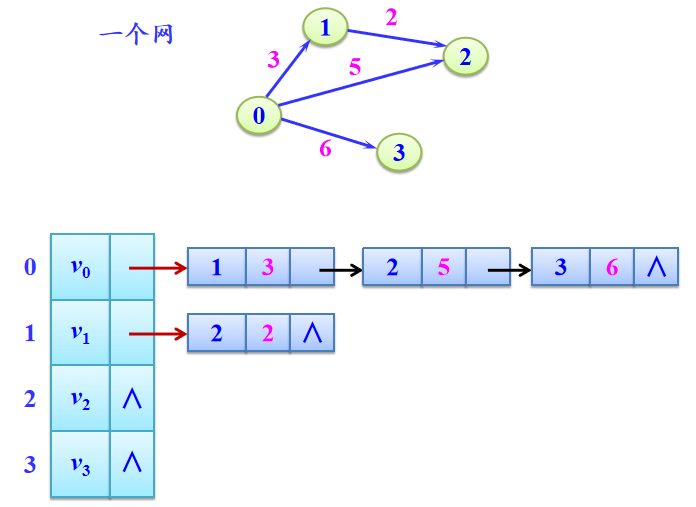
图4 带权有向图的邻接表存储结构图
图的邻接表存储类型定义如下:
typedef struct ANode
{ int adjvex; //该边的终点编号
struct ANode *nextarc; //指向下一条边的指针
int weight; //该边的权值等信息
} ArcNode;
typedef struct Vnode
{ Vertex data; //顶点信息
ArcNode *firstarc; //指向第一条边
} VNode;
typedef struct
{ VNode adjlist[MAXV] ; //邻接表
int n, e; //图中顶点数n和边数e
} AdjGraph;
一个邻接表通常用指针引用:
带权有向图的邻接表 
给定指向该结构的指针G,就可以对图进行操作。
图的遍历
所谓图的遍历(graph traversal),也称为搜索(search),就是从图中某个顶点出发,沿着一些边访遍图中所有的顶点,且使每个顶点仅被访问一次。遍历可以采取两种方法进行:深度优先搜索(DFS,depth first search)和广度优先搜索(BFS,breadth first search)。
广度优先遍历过程:
广度优先搜索(BFS,Breadth First Search)是一个分层的搜索过程,没有回退过程,是非递归的。其访问过程如下:
(1)访问初始点v, 接着访问v的所有未被访问过的邻接点v1, v2, …, vt。
(2)按照v1, v2, …, vt的次序, 访问每一个顶点的所有未被访问过的邻接点。
(3)依次类推, 直到图中所有和初始点v有路径相通的顶点都被访问过为止。
算法设计思路:
广度优先搜索遍历体现先进先出的特点, 用队列实现。
广度优先搜索过程 
如何确定一个顶点是否访问过? 设置一个visited[] 全局数组, visited[i]=0表示顶点i没有访问; visited[i]=1表示顶点i已经访问过。
BFS伪代码——邻接表实现
如果用邻接表存储图,则 BFS 算法实现的伪代码如下:
BFS(图 G, 顶点 i ) //从顶点 i 进行广度优先搜索
{
visited[ i ] = 1; //将顶点 i 的访问标志置为 1
将顶点 i 入队列;
while( 队列不为空 )
{
取出队列头的顶点,设为 k
p = 顶点 k 的边链表表头指针
while( p 不为空 )
{
//设指针 p 所指向的边结点所表示的边的另一个顶点为顶点 j
if( 顶点 j 未访问过 )
{
将顶点 j 的访问标志置为 1
将顶点 j 入队列
}
p = p->nextarc; //p 移向下一个边结点
} //end of while
} //end of while
} //end of BFS
对图1运行该算法的结果(从顶点2出发): 2 1 3 4 0。
编程要求
请你在右侧的代码窗口中实现bfs.cpp里的void BFS( AdjGraph* G, VertexType V)函数。 注意遵守约定:顶点编号小的先输出。
注:本关提供C++ STL队列容器queue,你可以直接使用。
测试说明
本关的测试过程如下:
1.平台编译 step2/bfs.cpp 并生成可执行文件;
2.平台运行该可执行文件,并以标准输入方式提供测试输入;
3.平台获取该可执行文件的输出,然后将其与预期输出对比,如果一致则测试通过;否则测试失败。
输入输出格式说明:
输入格式:
输入V,开始遍历的起始顶点编号。
输出格式:
输出对图进行广度优先遍历的顶点序列,每个顶点编号前面有一个空格。
以下是平台对 step2/bfs.cpp 的测试样例:
样例输入:
无向图
测试输入:2
样例输出:
预期输出:BFS from 2: 2 0 3 5 4 1 6
开始你的任务吧,祝你成功!
完整代码
#include "bfs.h"
/*
* 从顶点V出发进行广度优先搜索。
* 函数BFS应从编号为V的顶点出发广度优先遍历图,
* 遍历访问邻接点时,要求按序号递增的顺序。
* 题目保证V是图中的合法顶点。
*/
void BFS( AdjGraph* G, VertexType V)
{
/*******************begin*******************/
int k; // 队列头顶点
int i=V;
ArcNode *p; // 链表
// 初始化队列 队列保存访问过的顶点
queue<int> qu;
// 初始化visited数组
int visited[MAXV];
for(int b=0; b<G->n; b++){
visited[b]=0;
}
printf(" %d", i);
visited[i]=1;
// 开始BFS
qu.push(i);
while(!qu.empty()){
k = qu.front();
qu.pop();
p = G->adjlist[k].firstarc;
while(p!=NULL){
if(visited[p->adjvex]==0){ // 当前节点未访问
printf(" %d", p->adjvex);
visited[p->adjvex]=1;
qu.push(p->adjvex);
}
p=p->nextarc;
}
}
/*******************end*******************/
}
int main()
{
AdjGraph* G;
VertexType V;
G = CreateGraph();
scanf("%d", &V);
printf("BFS from %d:", V);
BFS(G, V);
return 0;
}
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 深入理解Java源码:提升技术功底,深度掌握技术框架,快速定位线上问题
- 网站安全每日话题——网页内容被篡改怎么办
- 峨眉山美食:罗鸭儿治愈挑剔味蕾
- 关于pygame无法打开对应文件解决办法 pyame.error unable to open file
- 新品|带同轴光远心镜头发布,专攻小物体高精度检测
- 数据分析:继loopy、卡皮巴拉后,小红书下个可爱“顶流”是?
- 面试宝典之JVM优化
- 《WebKit 技术内幕》之二: HTML 网页和结构
- Allegro在走线时有很多断线(有个小方框)如何处理?
- leetCode算法—7. 整数反转