数字拆分--完全背包问题

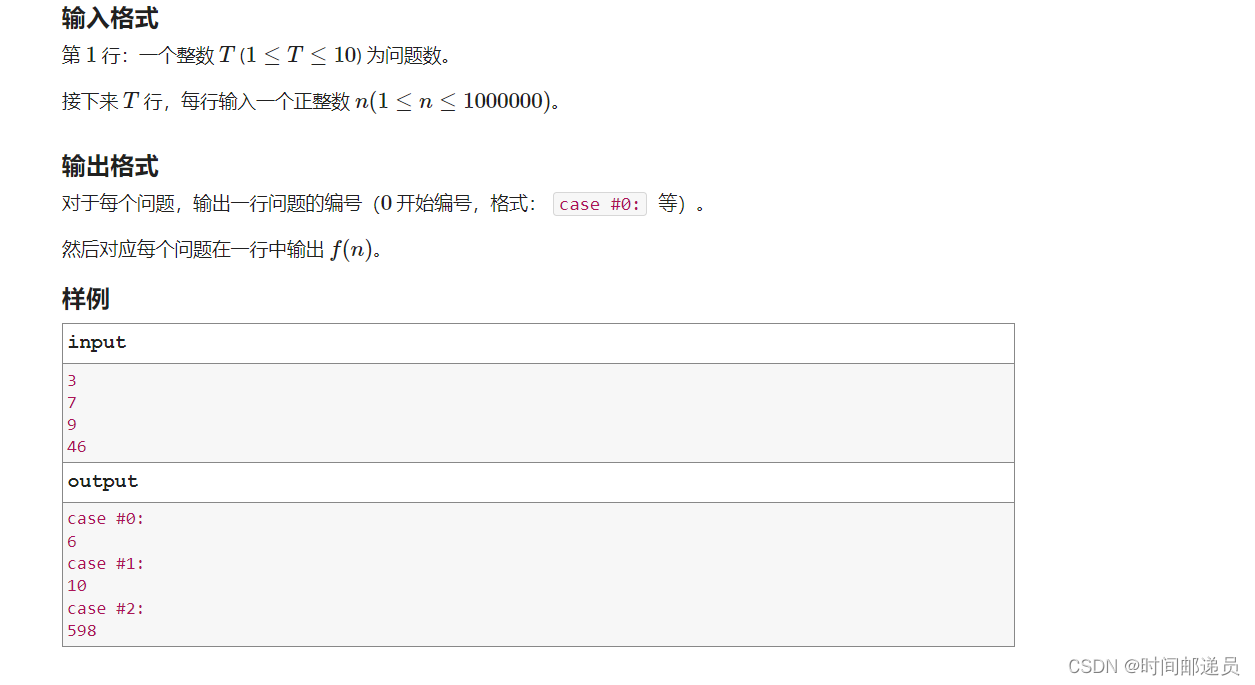
一、题目

https://acm.ecnu.edu.cn/problem/3034/

二、思路

本来算法就很弱，加上很久没刷题，做这道题真的是一言难尽~

一开始我以为是找规律写递推式，写到f(9)的时候就觉得不对劲，又想了一会，还是没想到，终究还是低头去看了评论，一看完全背包问题，死去的记忆开始攻击我，于是我又先去看01背包问题，还记得很久之前刷背包问题时，最难理解的就是为什么可以优化成一维以及为什么要逆序，我想这两个问题的解答CSDN、B站都写烂了，我就贴两个我觉得写的挺好的帖子吧，供大家参考

AcWing 2. 01背包问题（状态转移方程讲解） - AcWing

动态规划专题——背包问题_动态规划背包问题-CSDN博客

最后贴上这道题的Java解法，至于为什么要取余，我也是看了评论里的，都说题目漏了这个条件，不然数据会爆

import java.util.Scanner;

public class Main {
    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        int t = scanner.nextInt();
        int mod = 1000000000;
        for (int k = 0; k < t; k++) {
            System.out.println("case #" + k + ":");
            int n = scanner.nextInt();
            int[] dp = new int[n + 1];//dp[j]表示大小为j的值能够拆分的方案数量
            dp[0] = 1;//初始值
            for (int i = 1; i <= n; i *= 2) {//类似于背包问题中物品的体积
                for (int j = i; j <= n; j++) {
                    dp[j] = (dp[j - i] + dp[j]) % mod;
                }
            }
            System.out.println(dp[n]);
        }
    }
}