day06 有效的字母异位词 两个数组的交集 快乐数 两数之和

题目1：242 有效的字母异位词

题目链接：242 有效的字母异位词

题意

判断字符串t是否是字符串s的字母异位词? (字母异位词：s和t中每个字符串出现母次数都相同，且仅包含小写字符)?

数组

a~z是连续的? 所以可以映射到数组的下标即? a->0? b->1......z->25? 所以定义hash数组为hash[26]

先遍历第一个字符串每个字母出现的频率，再遍历第二个字符串，在第一个计算频率的基础上，减去第二个字符串相应的字母出现的频率

若最终的hash数组中每个下标处的元素值均为0，那么说明两个字符串互为异位词，否则，不是异位词

代码

class Solution {
public:
    bool isAnagram(string s, string t) {
        int hash[26] = {0};  //初始化为0
        for(int i=0;i<s.size();i++){
            hash[s[i]-'a']++;
        }
        for(int j=0;j<t.size();j++){
            hash[t[j]-'a']--;
        }
        for(int i=0;i<26;i++){
            if(hash[i]!=0){
                return false;
            }
        }
        return true;  
    }
};

• 时间复杂度: O(n)
• 空间复杂度: O(1)，因为定义的是一个常量大小的辅助数组

题目2： 349 两个数组的交集

题目链接：349 两个数组的交集

题意

求数组nums1 和 nums2的交集? 输出结果中的元素不重复，不考虑顺序

1<=nums1.length,nums.length<=1000? ? ?0<=nums1[i],nums2[i]<=1000

数组

将nums1数组放置到哈希表(数组)中，然后再遍历第二个数组nums2，判断nums2中的元素是否在nums1中出现过，若出现过，就放到result数组中

最终的结果使用unordered_set保存，可以去重

代码

class Solution {
public:
    vector<int> intersection(vector<int>& nums1, vector<int>& nums2) {
        unordered_set<int> result; //使用unordered_set数据结构可以去重
        int hash[1001] = {0};
        for(int i=0;i<nums1.size();i++){
            hash[nums1[i]] = 1; //将nums1中的元素存放到哈希表hash数组中
        }
        for(int i=0;i<nums2.size();i++){
            if(hash[nums2[i]]==1){
                result.insert(nums2[i]); //遍历nums2数组，在nums1的hash表中进行查找
            }
        }
        return vector<int>(result.begin(),result.end());
    }
};

• 时间复杂度: O(m + n)
• 空间复杂度: O(n)

set

将nums1数组中的元素放置到哈希表(unordered_set)中，然后遍历nums2数组 ，看在nums2中是否可以找到元素和存放在哈希表(unordered_set)的元素一致，如果找到，就放入到result，result也是unordered_set结构，可以去重

代码

class Solution {
public:
    vector<int> intersection(vector<int>& nums1, vector<int>& nums2) {
        unordered_set<int> result; //使用unordered_set数据结构可以去重
        unordered_set<int> nums_set(nums1.begin(),nums1.end()); //将nums1放入到哈希表set中,可以去重
        //遍历nums2数组，看在nums2中是否可以找到元素与nums1中元素相等
        for(int i=0;i<nums2.size();i++){
            if(nums_set.find(nums2[i])!=nums_set.end()){
                result.insert(nums2[i]); //遍历nums2数组，在nums1的hash表中进行查找
            }
        }
        return vector<int>(result.begin(),result.end());
    }
};

• 时间复杂度: O(n + m) m 是最后要把 set转成vector
• 空间复杂度: O(n)

题目3：202?快乐数

题目链接：202 快乐数

题意

判断n是否为快乐数

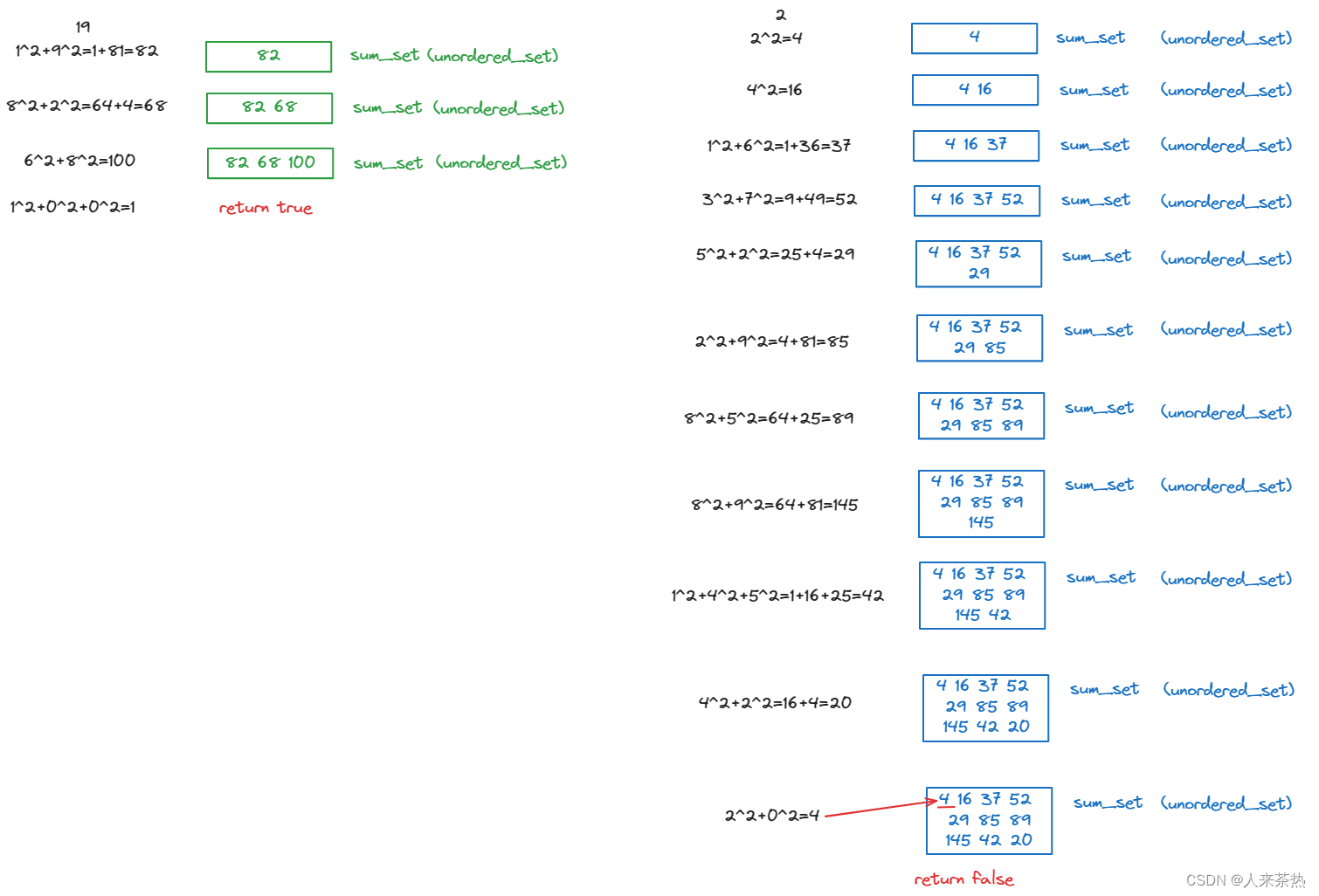
快乐数：正整数n 替换为各个位的平方和sum，一直重复这个求和替换的过程直到数字变为1，如果可以变为1，则n是快乐数；sum也可能无限循环，变不到1，则不是快乐数

关键：无限循环，sum一定会重复出现，使用哈希表

原因：n的取值范围是[1，2^31-1]，2^31-1=2147483647，一共10位，这10位中每一位最大取值是9，所以平方和最大是9^2*10=810，因为2147483647<999999999，所以重复的过程中，各个位的平方和小于810，无论重复多少次，各个位的平方和的取值是有限的，一定在[1,810]之间，是有限值。

所以，这说明非快乐数的n，对应的sum会重复出现，因此，可以使用哈希表判断一个元素是否重复出现在集合里

如果无限循环，说明sum会重复出现，则不是快乐数，如果没有重复，则是快乐数

数组

代码

class Solution {
public:
    int getsum(int n){
        int sum = 0;
        while(n){
            sum += (n%10) * (n%10);
            n = n/10;
        }
        return sum;
    }
    bool isHappy(int n) {
        int hash[810] = {0};
        while(1){
            int sum = getsum(n);
            if(sum==1){
                return true;
            }
            if(hash[sum]==1){
                return false;
            }//如果sum下标在hash数组中的元素为1，说明这个sum在hash中已经出现过
            //不能先赋值再查找，因为已经赋值了，再查找的话，肯定能找见
            hash[sum] = 1;
            n = sum;//记得最终更新n，继续下一次循环
        }
    }
};

set

本题的元素数值较大且还需要判断元素是否重复出现，因此使用unordered_set

代码

class Solution {
public:
    int getsum(int n){
        int sum = 0;
        while(n){
            sum += (n%10) * (n%10);
            n = n/10;
        }
        return sum;
    }
    bool isHappy(int n) {
        unordered_set<int> sum_set;
        while(1){
            int sum = getsum(n);
            if(sum==1){
                return true;
            }
            if(sum_set.find(sum)!=sum_set.end()){
                return false;
            }//这里一定要先找sum,如果找到了直接false
            //不能先插入再查找，因为已经插入了，再查找的话，肯定能找见
            sum_set.insert(sum);
            n = sum;//记得最终更新n，继续下一次循环
        }
    }
};

• 时间复杂度: O(logn)
• 空间复杂度: O(logn)

题目4：1 两数之和

题目链接：1 两数之和

题意

找出nums数组中和为target的两个整数，返回对应的下标，数组中的元素不能重复使用

每种输入只会对应一个答案，这一点很重要

以上的这个数组就不满足要求，因为这个数组中有3个对应的答案，所以不满足要求

暴力解法

因为题目的数值较大且数值较为分散，所以首先想到了使用set解决

set

步骤

① 循环遍历数组的元素，求解target-nums[i]，将差值存放在哈希表中

由于unordered_set可以去重并且增删查的效率很高，因此哈希表使用unordered_set

② 遍历该元素之后的各个元素，查看数组中是否有元素和差值相等，即判断数组的元素是否在set中出现过，如果存在，就将下标记录下来，紧接着，一定要记着删除放在det中的差值，因为我们始终要找的是当前的差值和数组中该元素之后的元素是否相等，如果set中一直保留以前的差值，可能会对结果产生干扰

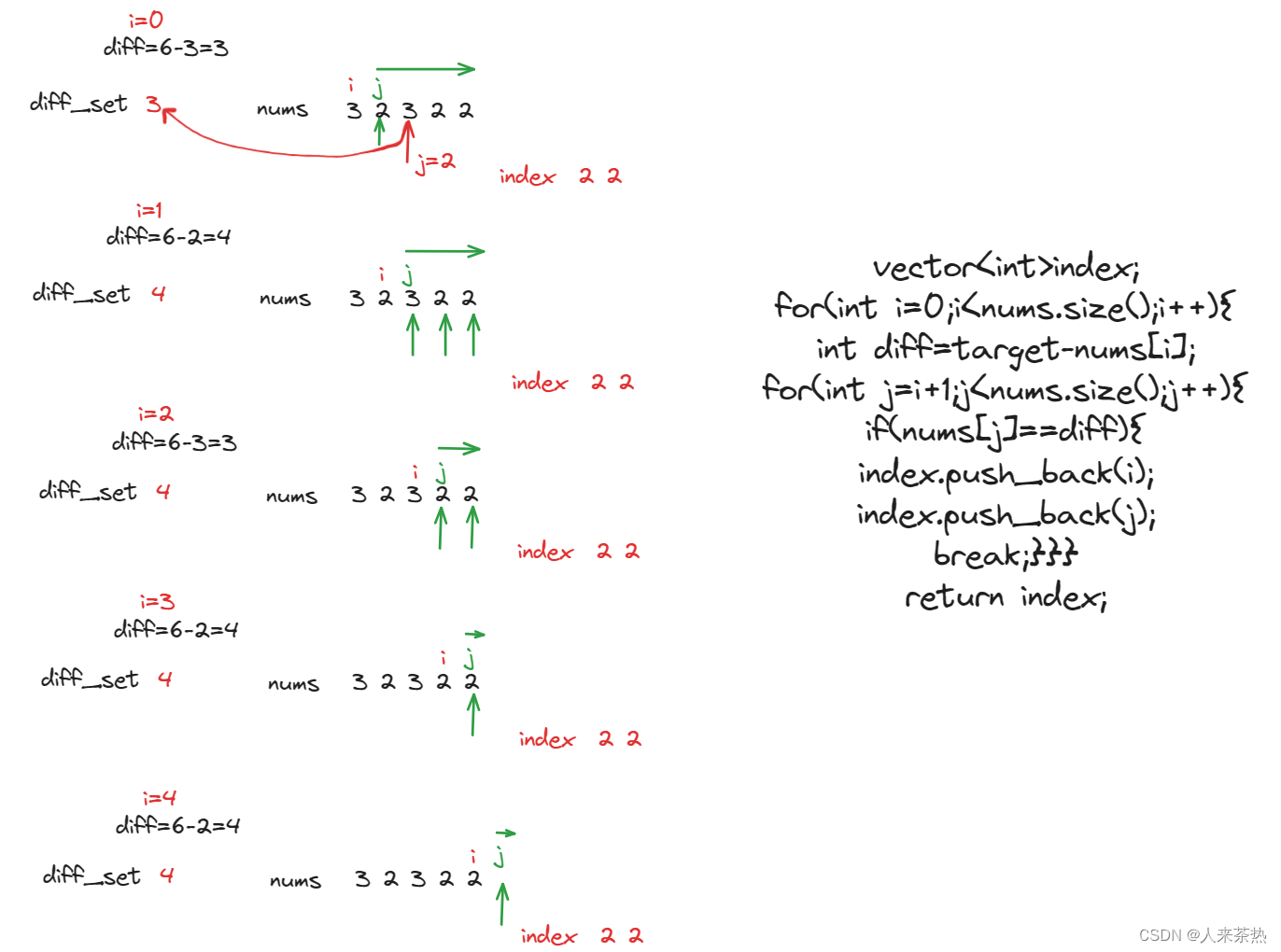
下面的案例就是开始报错的案例，就是因为一直保留set中的值，所以出现了错误，不同组的元素查找同一个diff，图左就是一个典型，解决的方法就是把已经匹配到的diff元素从set中删除，这样相同的元素（3+3=6，4+4=8......）就不会重复查找到了

伪代码

代码

class Solution {
public:
    vector<int> twoSum(vector<int>& nums, int target) {
        unordered_set<int> diff_set;//定义一个set存放差值
        vector<int>index;//存放最终的下标
        for(int i=0;i<nums.size();i++){  //这里写nums.size()-1也可，因为最后一个元素，判不判定都无所谓，后面没有与之匹配的元素了
            int diff = target - nums[i];  //差值
            diff_set.insert(diff);   //将差值放入到set
            for(int j=i+1;j<nums.size();j++){   //遍历当前元素之后的元素
                if(diff_set.find(nums[j])!=diff_set.end()){//在之后的元素找到了等于差值的元素
                    index.push_back(i);//存放下标
                    index.push_back(j);
                    diff_set.erase(diff);//！！！因为会有重复数字的过程 如果不删除的话就会错误查找，这一步很重要，diff改为nums[j]也可，两者相等       
                    break;
                }
            }
        }  
        return index; 
    }
};

• 时间复杂度: O(n^2)，两层for循环
• 空间复杂度: O(n)

数组

基于以上set的方法的原理，想到可以用到数组，将diff差值直接放到数组中。

这个解法和直接暴力解法相同，只是将数值放到了大小为1的数组中，其实这样并没有意义，但是因为这节学了哈希表，先想到了把差值diff放到数组中，后来才想到直接暴力的想法，学的还是有点死了

代码1（使用vector容器）

class Solution {
public:
    vector<int> twoSum(vector<int>& nums, int target) {
        vector<int> diff_result;//定义一个数组存放差值
        vector<int>index;//存放最终的下标
        for(int i=0;i<nums.size();i++){  //这里写nums.size()-1也可，因为最后一个元素，判不判定都无所谓，后面没有与之匹配的元素了
            int diff = target - nums[i];  //差值
            diff_result.push_back(diff);   //将差值放入到数组中
            for(int j=i+1;j<nums.size();j++){   //遍历当前元素之后的元素
                if(nums[j]==diff_result[0]){//在之后的元素找到了等于差值的元素
                    index.push_back(i);//存放下标
                    index.push_back(j);
                    break;
                }
            }
            diff_result.pop_back();//！！因为会有重复数字的过程 如果不删除的话就会错误查找，这一步很重要
        }  
        return index; 
    }
};

• 时间复杂度: O(n^2)，两层for循环
• 空间复杂度: O(n)

代码2(基于上述的vector容器，想到也可以使用int型数组hash[0]，只包含一个元素)

class Solution {
public:
    vector<int> twoSum(vector<int>& nums, int target) {
        int hash[1];//定义一个数组存放差值
        vector<int>index;//存放最终的下标
        for(int i=0;i<nums.size();i++){  //这里写nums.size()-1也可，因为最后一个元素，判不判定都无所谓，后面没有与之匹配的元素了
            int diff = target - nums[i];  //差值
            hash[0] = diff;   //将差值放入到数组中
            for(int j=i+1;j<nums.size();j++){   //遍历当前元素之后的元素
                if(nums[j]==hash[0]){//在之后的元素找到了等于差值的元素
                    index.push_back(i);//存放下标
                    index.push_back(j);
                    break;
                }
            }
        }  
        return index; 
    }
};

• 时间复杂度: O(n^2)，两层for循环
• 空间复杂度: O(n)

直接

基于以上的hash数组中，只包含1个元素，想到使用直接暴力方法，绕了一个大弯😂

代码

class Solution {
public:
    vector<int> twoSum(vector<int>& nums, int target) {
        vector<int>index;//存放最终的下标
        for(int i=0;i<nums.size();i++){  //这里写nums.size()-1也可，因为最后一个元素，判不判定都无所谓，后面没有与之匹配的元素了
            int diff = target - nums[i];  //差值
            for(int j=i+1;j<nums.size();j++){   //遍历当前元素之后的元素
                if(nums[j]==diff){//在之后的元素找到了等于差值的元素
                    index.push_back(i);//存放下标
                    index.push_back(j);
                    break;
                }
            }
        }  
        return index; 
    }
};

• 时间复杂度: O(n^2)，两层for循环
• 空间复杂度: O(n)

map

既要知道元素是否在数组中出现过，还要知道下标，因此使用key-value结构较合适，map比较合适 ，key存放元素，根据key就可查询这个元素是否出现过；value存放下标，如果key出现过，那么返回对应的value

！！！map存放的是遍历过的元素！！！这一点很重要

使用unordered_map，读写的效率很高

这个思路和暴力解法的思路不一样，暴力解法找的是该元素之后的元素，而map存放的是已经遍历的元素，查询的是之前已经遍历的元素。

遍历元素时，查询map中是否有与当前元素（diff）相匹配的元素，如果有，则直接return;没有的话，就将当前元素nums[i]及其下标i放到map中。

代码

class Solution {
public:
    vector<int> twoSum(vector<int>& nums, int target) {
        unordered_map<int,int> map;//存放遍历过的元素 key value
        for(int i=0;i<nums.size();i++){
            int diff = target - nums[i];//差值
            auto inter = map.find(diff);//在map中寻找是否出现过与该元素nums[i]对应的差值(key)
            //inter含有key value两个元素
            if(inter!=map.end()){//在map中找到了元素nums[i]对应的差值(key)，所以找到了一组元素(key value)
                return {inter->second,i};
                break;//因为只有1组满足
            }
            // else{
            //     map.insert(pair<int,int>(nums[i],i));
            // }
            map.insert(pair<int,int>(nums[i],i));//这段代码放到else里面也可以，还是因为只有1对，因为if里面已经return了，所以else和不else均可，所以可以这样操作
        }
        return {};
    }
};

• 时间复杂度: O(n)
• 空间复杂度: O(n)