5_机械臂运动学基础_矩阵

上次说的向量空间是为矩阵服务的。

1、学科回顾

? 从科技实践中来的数学问题无非分为两类：一类是线性问题，一类是非线性问题。线性问题是研究最久、理论最完善的；而非线性问题则可以在一定基础上转化为线性问题求解。

线性变换：

数域F上线性空间V中的变换T若满足条件：

T(a?+ b) = Ta?+ Tb????(a,b???V)

? ? ? ?T(ka) ?= kTa????????(k?? F, ?a?? V)

? ?则称T为V中的线性变换。

? 线性变换两方面的意义：变换空间里的向量，空间坐标系不变；或者变换坐标系而向量不变。两者是相对的，结果等价。

2、矩阵

? 作为一种新型的数学表示工具，是“比例函数”概念的推广，是描述向量之间变换关系的。比例函数的系数是“数”与“数”之间的线性对应关系，是把一个数变为另一个数，那么矩阵则是向量与向量之间的线性对应关系，是把一个向量变成另一个向量。

? 矩阵把一个向量变成另一个向量是发生在向量空间里的变换运动，该变换有个专业名词叫线性变换或线性映射。这可以称为矩阵的几何意义。

? 矩阵独立的几何意义表现为对向量的作用结果。矩阵对一个向量是如何作用的？矩阵对多个向量是如何作用的？矩阵对空间上的坐标基向量又是如何作用的？

? 一个矩阵就描述了向量空间中的一个运动——变换，这个矩阵规定了所有向量的变换规则。

2.1 矩阵与任意向量的乘积的几何解释

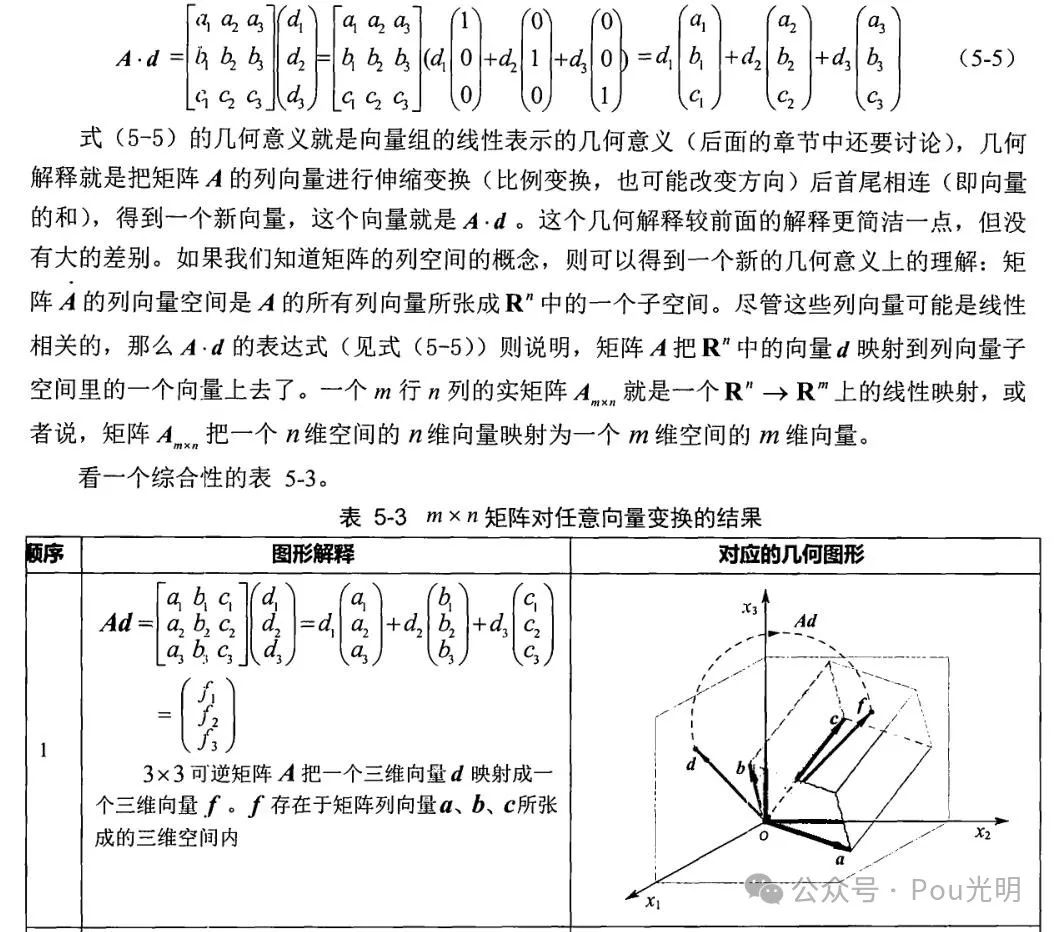
2.2 矩阵与矩阵乘法的几何意义

? 两个矩阵相乘，如AB的几何意义可以从多个角度来了解。如果把矩阵A看做一个几何图形，那么乘以B就是把A的图形进行了有规律的变换，这个变换就是线性变换(将矩阵A看做多个向量的组合)。如果把两个矩阵看做等同的，那么AB的结果是把两个线性变换进行了叠加或复合(机械臂6个变换矩阵连乘)。

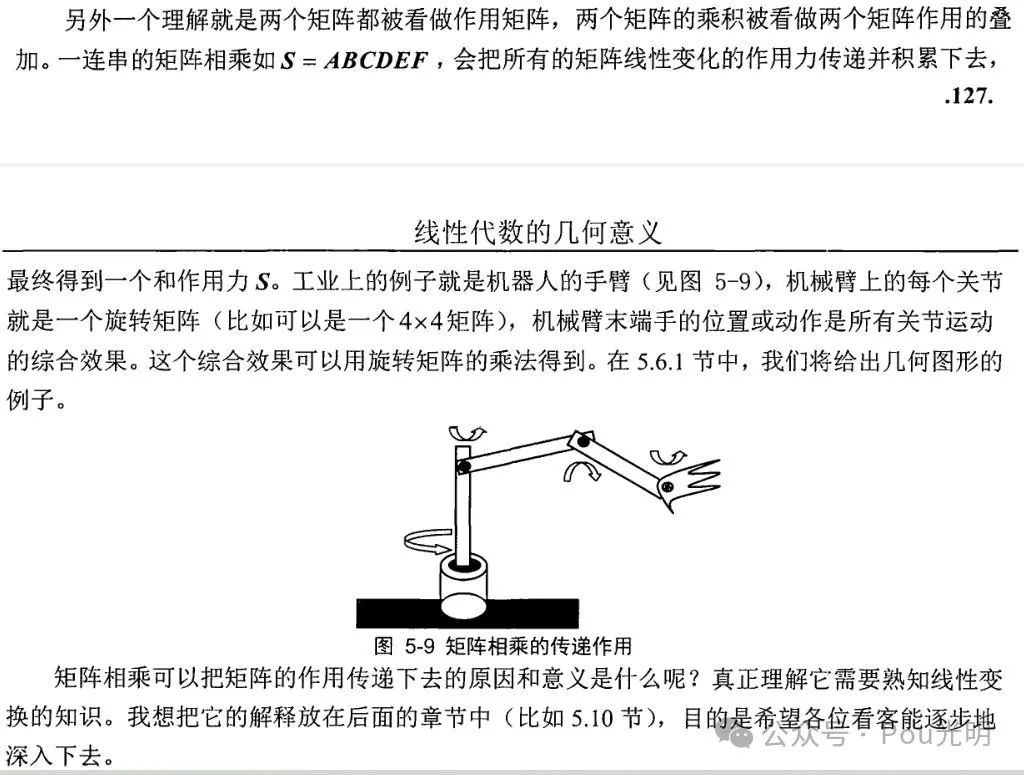
机械臂运行在3维空间，为什么是一个4×4的矩阵呢？

2.3 矩阵与线性变换关系的几何意义

m×n阶矩阵可表示把一个n维空间的向量映射到m维空间的向量的线性映射，而一个n阶方阵是把一个n维空间的向量映射到自身空间另外一个向量的线性变换。

2.3.1 线性变换如何用矩阵表示

举例说明：

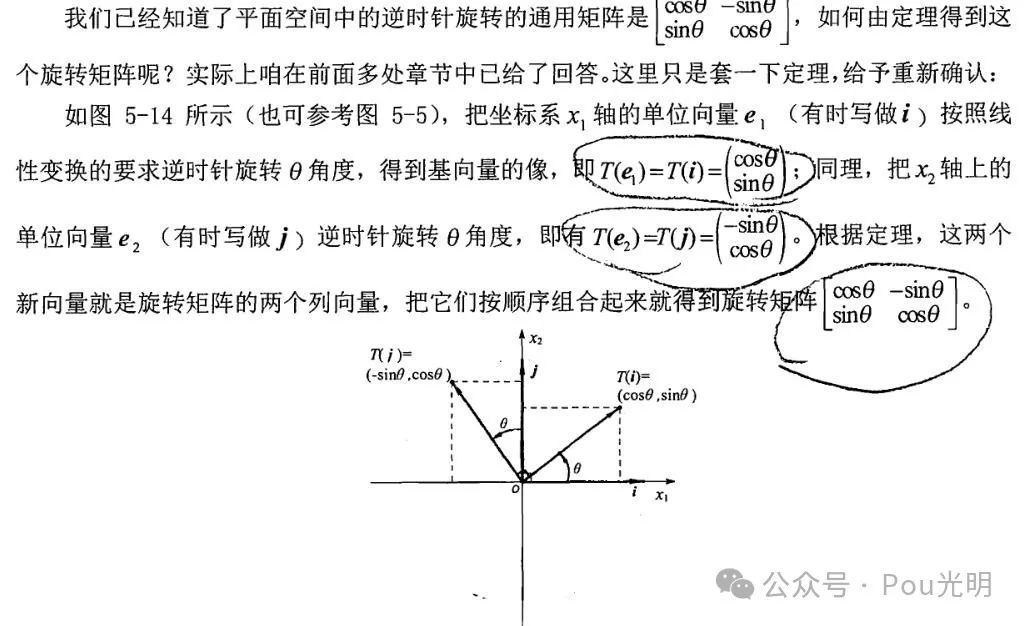
2.4 两个矩阵相乘是两个线性变换的复合

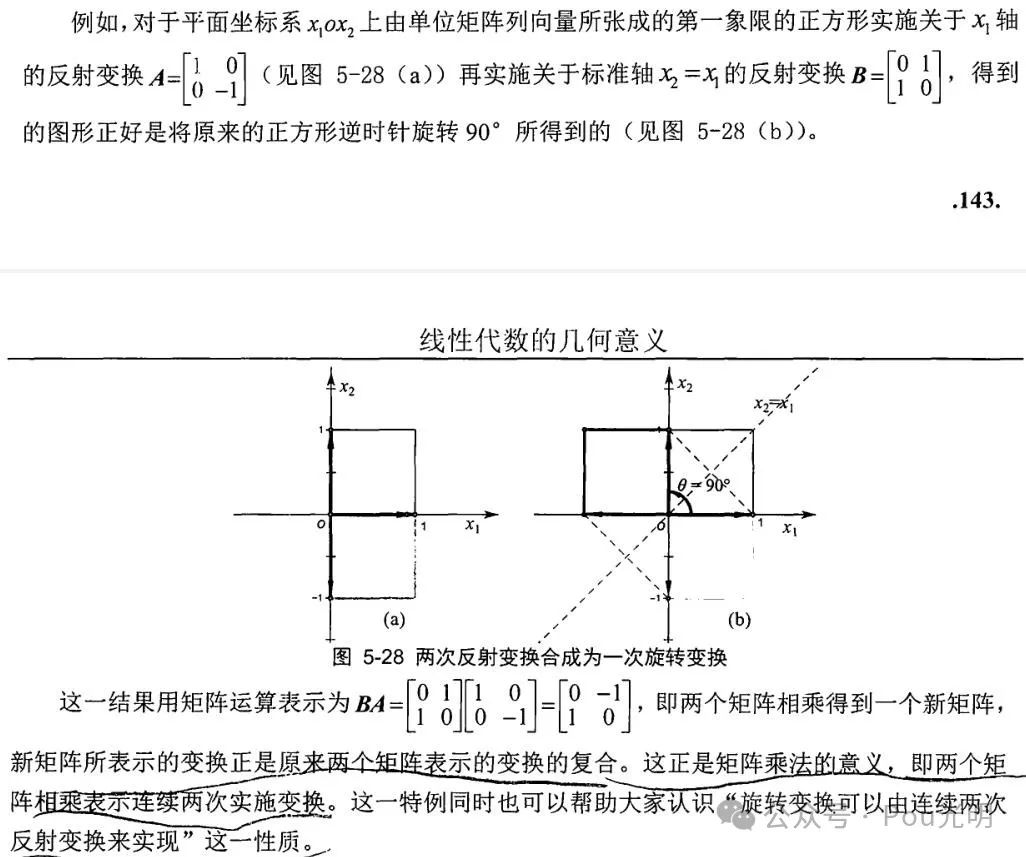
2.5 特征值和特征向量的几何意义

考研人很熟悉。

什么样的方阵对向量只有旋转而没有伸缩变化呢？它有什么特征呢？

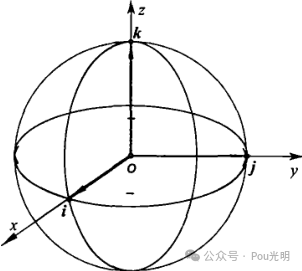
《线性代数的几何意义》——任广千

?? PS：推荐一个pdf阅读软件——SumatraPDF，可以直接选中印刷版的pdf复制，可以双击获取图片，还很小，不到23M。? ? ????