刷题总结 1.22

kmp算法完成的任务是：给定两个字符串O和f，长度分别为n和 m，判断f是否在O中出现，如果出现则返回出现的位置。

常规方法是遍历O的每一个位置，然后从该位置开始和f进行匹配，但是这种方法的复杂度O(nm)。kmp算法通过一个O(m)的预处理，使匹配的复杂度降为O(n+m)。

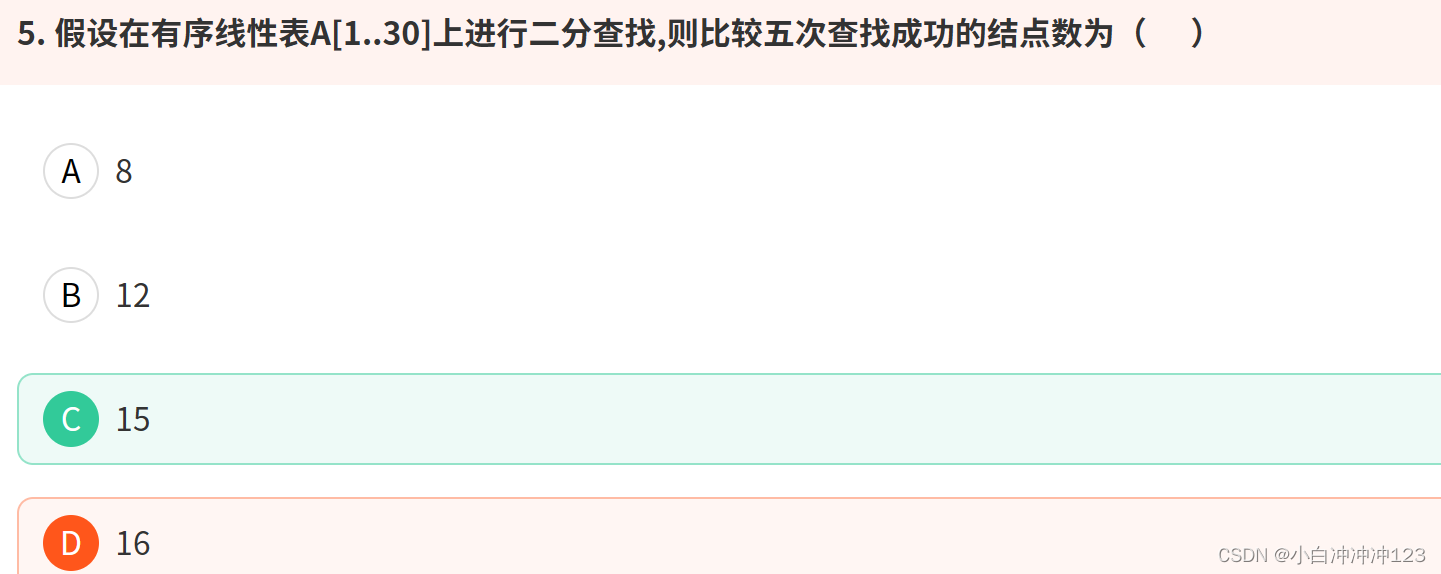
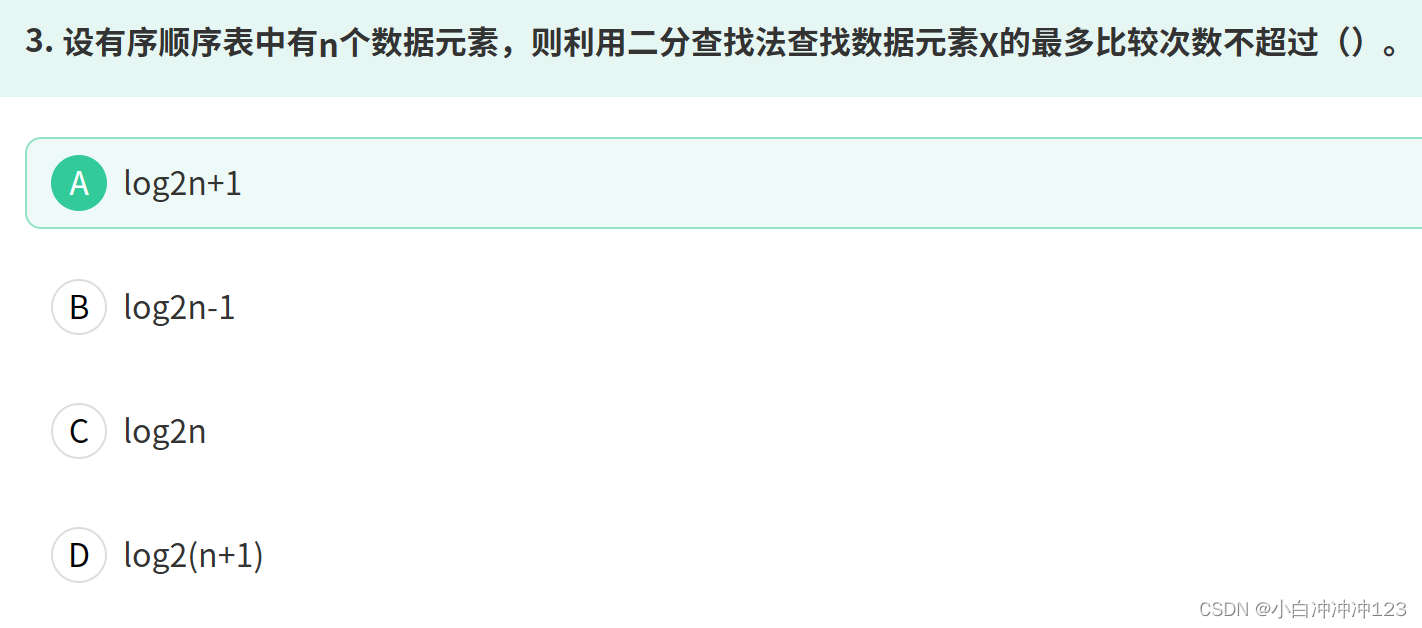
二分查找中的表中数据可以是任意类型的，只要能够进行比较操作即可。常见的数据类型可以是整数、浮点数、字符串等。对于自定义类型，可以通过定义比较函数或者重载比较操作符来实现比较操作。

最坏最好情况均为O(logN)

?尾递归是指，在函数返回的时候，调用自身本身，并且，return语句不能包含表达式。这样，编译器或者解释器就可以把尾递归做优化，使递归本身无论调用多少次，都只占用一个栈帧，不会出现栈溢出的情况。 尾递归调用时，如果做了优化，栈不会增长，因此，无论多少次调用也不会导致栈溢出。

以斐波那契数列为例子

普通的递归版本

int fab(int n){

? ? if(n<3)

? ? ? ? return 1;

? ??else

? ? ? ? return fab(n-1)+fab(n-2); ?

}

具有"线性迭代过程"特性的递归---尾递归过程

int fab(int n,int b1=1,int b2=1,int c=3){

? ? if(n<3)

? ? ? ??return 1;

? ? else {

? ? ? ??if(n==c)

? ? ? ? ? ? ?return b1+b2;

? ? ? ? else

? ? ? ? ? ? ?return fab1(n,b2,b1+b2,c+1);

? ? }

}

以fab(4)为例子

普通递归fab(4)=fab(3)+fab(2)=fab(2)+fab(1)+fab(2)=3 ?6次调用

尾递归fab(4,1,1,3)=fab(4,1,2,4)=1+2=3 ????????????????????????2次调用

假设走n步阶梯的方法总数为f(n)，那么对于n步的阶梯，有三种情况：第一步走一步，第一步走两步，第一步走三步。

?走完第一步后剩下的走法分别有f(n-1)，f(n-2)，f(n-3)种走法，

所以有: ?f(n)=f(n-1)+f(n-2)+f(n-3) ? ? ?(对于n>=4)?

?同理： f(n-1)=f(n-2)+f(n-3)+f(n-4) ?? (对于n>=5)?

?前面两式相减可以得到： ?f(n)=2*f(n-1)-f(n-4) ?(对于n>=5)

?而对于n<=5的情况有：?

?f(1)=1?

?f(2)=2?

?f(3)=4?

?f(4)=7?

于是有：?

f(5)=2*7-f(1)=13?

(6)=2*13-f(2)=24?

?f(7)=2*24-f(3)=44?

f(8)=88-f(4)=81?

f(9)=2*81-f(5)=149 <

f(10)=298-f(6)=274?

f(11)=548-f(7)=504?

f(12)=1008-f(8)=927?

f(13)=1854-f(9)=1854-149=1705?

?f(14)=3410-f(10)=3410-274=3136?

f(15)=6272-f(11)=6272-504=5768?