概率中的50个具有挑战性的问题[03/50]:轻率的陪审员
发布时间:2023年12月23日
一、说明
????????我最近对与概率有关的问题产生了兴趣。我偶然读到了弗雷德里克·莫斯特勒(Frederick Mosteller)的《概率论中的五十个具有挑战性的问题与解决方案》(Fifty Challenge Problems in Probability with Solutions)一书。我认为创建一个系列来讨论这些可能作为面试问题出现的迷人问题会很有趣。每篇文章只有 1 个问题,使其成为一个总共有 50 个部分的系列。让我们潜入并激活我们的脑细胞🧠!

图片由作者使用 DALL-E 3 提供。
二、问题描述
一个由三人组成的陪审团有两名成员,每个成员独立地有做出正确决定的概率p,第三名成员为每个决定掷硬币(多数规则)。一个人的陪审团有概率p做出正确的决定。
问:哪个陪审团更有可能做出正确的决定?
三、问题分解
????????让我们研究一下三人陪审团使用多数规则做出正确决定的情况(其中至少有两名成员做出准确的决定)。我们将指定负责掷硬币的成员为非严肃陪审员,而其他两名成员将被称为严肃陪审员。可能的情况如下:
????????让我们考虑一下三人陪审团使用多数规则做出正确决定的情况(其中至少有两个人必须做出正确的决定)。让我们把为决定抛硬币的成员称为轻率的陪审员,将另外两名成员称为严肃的陪审员。可能的情况如下:
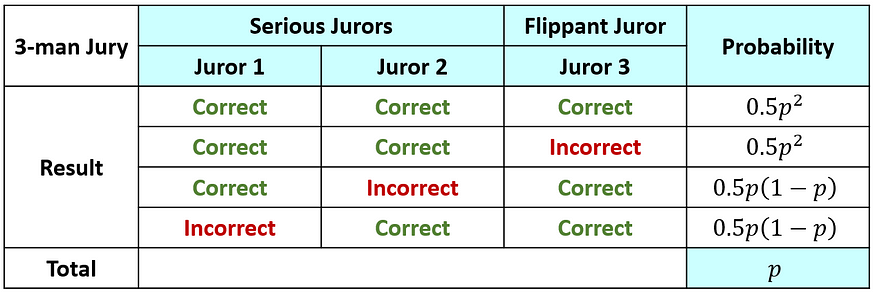
因此,我们得出结论,三人陪审团做出正确决定的总概率(p)等于一人陪审团做出正确决定的概率(p)。
Python 代码:
import numpy as np
n_trials = 10000000
for n in range(1,10):
p = n/10
correct_1 = np.random.binomial(1, p, size = n_trials) # serious juror
correct_2 = np.random.binomial(1, p, size = n_trials) # serious juror
correct_3 = np.random.binomial(1, 0.5, size = n_trials) # flippant juror
correct = ((correct_1 + correct_2 + correct_3)>=2).astype(int)
print('p={}, P(three-man jury is correct)={}'.format(p, round(np.mean(correct),3)))
# Outputs:
# p=0.1, P(three-man jury is correct)=0.1
# p=0.2, P(three-man jury is correct)=0.2
# p=0.3, P(three-man jury is correct)=0.3
# p=0.4, P(three-man jury is correct)=0.4
# p=0.5, P(three-man jury is correct)=0.5
# p=0.6, P(three-man jury is correct)=0.6
# p=0.7, P(three-man jury is correct)=0.7
# p=0.8, P(three-man jury is correct)=0.8
# p=0.9, P(three-man jury is correct)=0.9
这就是这个陪审团👨🏻 ??问题的全部内容。欢迎任何反馈或问题!该代码可在我的?Github?上找到。请继续关注本系列的下一部分!:)
文章来源:https://blog.csdn.net/gongdiwudu/article/details/135166417
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
最新文章
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- Jenkins Pipeline脚本优化:为Kubernetes应用部署增加状态检测
- 【学习笔记】JavaScript中的GC算法
- Ubuntu 22.04 安装cmake3.28
- 想在IDEA中调试API?试试这款,堪比postman
- 【Verilog】期末复习——数字逻辑电路分为哪两类?它们各自的特点是什么?
- 【Vue自定义指令详细介绍】
- Flask SQLAlchemy怎么查看参数化查询的实际SQL语句
- 2024 年 17 个提高生产力的 Chrome 扩展,你用了几个呢?
- Java版直播商城免 费 搭 建:电商、小程序、三级分销及免 费 搭 建,平台规划与营销策略全掌握
- Redis之集群方案比较