机器学习---PCA案例
发布时间:2024年01月04日
1. PCA
import numpy as np
from sklearn.decomposition import PCA
import matplotlib.pyplot as plt
from sklearn.datasets import load_digits
def pca(dataMat,topNfeat=9999999):
meanVals=np.mean(dataMat,axis=0)
# 去除平均值,实现数据中心化
meanRemoved=dataMat-meanVals
covMat=np.cov(meanRemoved,rowvar=0)
# 计算矩阵的特征值个特征向量
eigVals,eigVects=np.linalg.eig(np.mat(covMat))
eigValInd=np.argsort(eigVals)
# 从大到小对N个值排序
eigValInd=eigValInd[:-(topNfeat+1):-1]
redEigVects=eigVects[:,eigValInd]
# 将数据转换到新空间
lowDDataMat=meanRemoved*redEigVects
reconMat=(lowDDataMat*redEigVects.T)+meanVals
return lowDDataMat,reconMat
dataMat = np.array([[1,2,3], [4,2,1], [3,2,1]])
X = load_digits().data[:, :]
lowDDataMat,reconMat = pca(X,topNfeat=2)
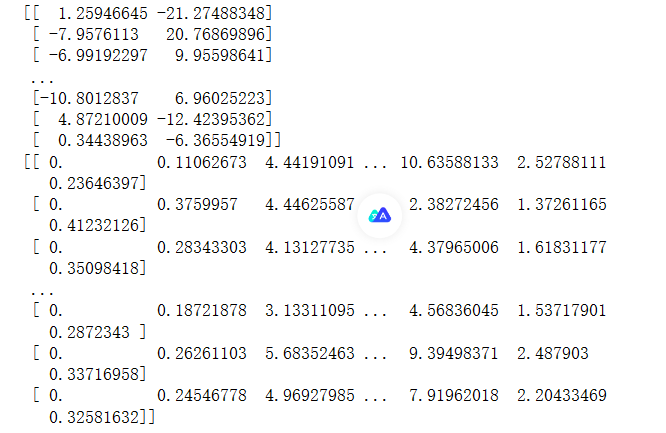
print(lowDDataMat)
print(reconMat)
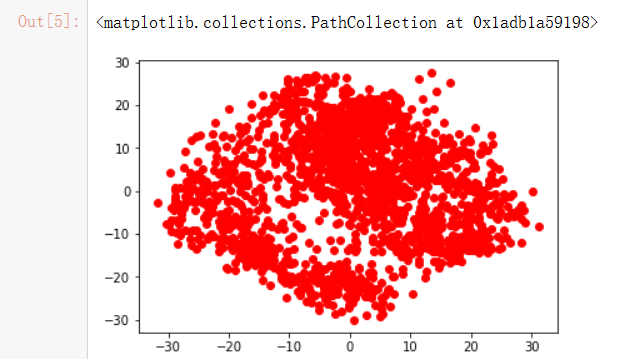
plt.scatter(lowDDataMat[:,0].tolist(), lowDDataMat[:,1].tolist(),c = 'r',marker = 'o')2个参数:一个参数是用于进行PCA操作的数据集,第二个参数是可选参数,即应用N个特征,首
先计算并减去原始数据集的平均值,然后计算协方差矩阵及其特征值,然后利用argsort函数对特征
值进行从小到大排序,根据特征值排序的逆序就可以得到最大的N个向量,这些向量将构成后面对
数据进行转换的矩阵,该矩阵则利用N个特征将原始数据转换到新空间中,最后原始数据被重构后
返回,同时,降维之后的数据集也被返回。
?
文章来源:https://blog.csdn.net/weixin_43961909/article/details/135384577
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
最新文章
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- Conda常用指令
- 高效图片管理系统的技术实现与优化策略
- Ps2022版DR5插件扩展窗口不展示及未正确签署等问题修复
- uni-app小程序:文件下载打开文件方法苹果安卓都适用
- 今年倒闭了1.09万家芯片公司....
- RK3568驱动指南|第十篇 热插拔-第116章netlink监听广播信息实验
- 【算法分析与设计】最大子数组和
- 手机常用的root方案
- BART论文解读:BERT和GPT结合起来会发生什么?
- openGauss学习笔记-162 openGauss 数据库运维-备份与恢复-导入数据-通过INSERT语句直接写入数据