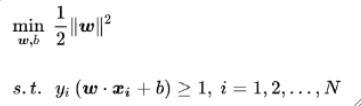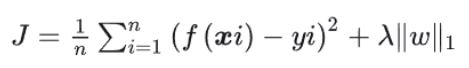机器学习期末复习总结笔记（李航统计学习方法）

模型复杂度高—过拟合

• 是什么：当模型复杂度越高，对训练集拟合程度越高，然而对新样本的泛化能力却下降了，此时出现overfitting（过拟合）
• 与泛化能力：
  • 模型复杂度与泛化能力之间存在权衡关系。过于复杂的模型可能导致过拟合，而过于简单的模型可能导致欠拟合。理想的情况是找到二者之间的平衡点，以最佳化模型的泛化能力
• 产生原因：对训练数据中的噪声和特定特征过度敏感。
  • 训练样本太少
  • 数据的特征过多
  • 选择的模型比较复杂、模型参数过多
  • 缺乏正则化
• 解决：
  • 正则化
  • 减少特征数、减少模型参数、增加训练样本
• 欠拟合：
  • 概述：对训练数据和新数据均表现不佳
  • 原因：
    • 训练次数不够
    • 特征太少
    • 模型简单
  • 解决
    • 训练次数增加
    • 添加新特征
    • 增加模型复杂度
    • 减小正则化系数（可以减轻对模型复杂度的限制，允许模型参数有更大的变化范围）

分类与回归

• 分类：输出值为离散数据、寻找决策边界
  • 指标：准确率、精确率P、召回率R、F1值
• 回归：输出值为连续数据、寻找最佳拟合
  • MSE均方误差、RMSE均方根误差、MAE平均绝对误差

有监督、无监督、半监督

• 有监督：有label
• 无监督：无label，（聚类、PCA）
• 半监督：少量label、大量无label，利用标注数据中的信息，辅助标注数据，进行监督学习，以较低的成本达到较好的学习效果

正则化

• 定义：在经验风险上加上一个正则项（罚项），其通常与模型权重的大小有关
• 分类：
  • L1（Lasso回归）：稀疏，特征选择，解释性强
  • L2（Ridge岭回归）：抗噪声能力强
  • 都能控制过拟合
• 作用：
  • 防止过拟合：选择经验风险与模型复杂度同时较小的模型，防止过拟合，从而提高模型泛化能力
  • 有助于特征选择：L1，促使模型在训练过程中自动进行特征选择
  • 提高稳定性：L2，对输入数据的小变化不敏感，提高模型稳定性

生成模型和判别模型

• 判别模型：学习条件概率分布P(Y|X)
• 生成模型：学习联合概率分布P(X,Y)
• 总之，判别式模型和生成式模型的最终目的都是使后验概率最大化，其中判别式是直接对后验概率建模，而生成式模型通过贝叶斯定理这一“桥梁”使问题转化为求联合概率。

感知机

• 损失函数：误分类点到超平面的距离之和（去掉了分母的范数、加个负号）
• 随机梯度下降：求偏导：参数更新公式：w=w+ayx, b=b+ay
• 学习算法
  • 初始w和b、a（学习率）
  • 若满足y(wx+b)<=0，则为误分类点，更新w和b
  • 直至没有误分类点
• 学习算法收敛性
  • 当数据线性可分，误分类的次数是有上界的，原始迭代形式是收敛的
  • 当数据线性不可分，迭代震荡
  • 解不唯一（初始w、b，以及误分类点的选择）

KNN

• K-nearest-neighbor：k=1为最近邻
• K值选择
  • k小：模型复杂，过拟合
  • k大：模型简单
• 距离度量：
  • 曼哈顿、欧式距离
• 分类决策：多数表决

朴素贝叶斯

• 朴素：特征条件独立性
• 拉普拉斯平滑（分子+1，分母+K，K为某个特征的类别数）
• 后验概率最大化 等价于 0-1损失函数期望风险最小化
• 计算题：
  • 先验概率 P(Y=y1) …
  • 条件概率 P(X1=x1 | Y=y1) …
  • 先验概率×条件概率

决策树

• 概念计算
  • 信息量
  • 熵
  • 条件熵
  • 信息增益
  • 基尼指数
  • 基尼指数是CART算法中用来衡量分割后数据纯度的标准，反映了从数据集中随机抽取两个样本，其类别标签不一致的概率。信息增益则是ID3算法中用于选择特征的标准，衡量的是分割前后数据不确定性的减少量。基尼指数更偏重于数据的纯净度，而信息增益更关注信息的减少量。
• 特征选择、树的生成
  • ID3：信息增益（选大的）
    • 只能离散型数据
    • 容易过拟合（无剪枝策略）
    • 对可取值数目较多的特征有所偏好，类似“编号”的特征其信息增益接近于 1
    • 多叉树
  • C4.5：信息增益比（选大的）
    • 连续、离散数据
    • 引入剪枝策略（后悔法，效率低）
    • 最大的特点是克服了 ID3 对特征数目的偏重这一缺点
    • 只能分类
    • 多叉树
  • CART：基尼指数（选小的）
    • 连续、离散数据
    • 剪枝效果更好
    • 分类＋回归
    • 二叉树
• 剪枝
  • 预剪枝：容易欠拟合
  • 后剪枝：效果好

SVM

• 间隔
  • 函数间隔：y(wx+b)， 点到超平面的“确信度”
  • 几何间隔：y(wx+b) / ||w||，点到超平面的实际距离
  • 硬间隔：硬间隔SVM要求所有数据点都严格正确地分类，模型试图完美地分类所有样本，对于含有噪声或异常值的数据集会过拟合
  • 软间隔：软间隔SVM允许某些数据点违反边界间隔的要求，即允许一些点位于边界的错误一侧或在间隔内。更好地处理噪声和异常点，提高模型的泛化能力。
• 最优化问题
  • 
  • 推导过程见书
• 与感知机的区别：
  • 感知机：误分类最小化，分离超平面很多，线性可分数据，不支持核技巧
  • 支持向量机：间隔最大化，最优（几何间隔最大）分离超平面唯一，可线性可非线性，支持核技巧
• 分类
  • 线性可分支持向量机：硬间隔最大化
  • 线性支持向量机：训练数据近似线性可分时，通过软间隔最大化
  • 非线性支持向量机：当训练数据线性不可分时，通过使用核技巧及软间隔最大化
• 核函数：
  • 核技巧的作用是将原始数据映射到更高维的空间，使得在新空间中数据线性可分，从而有效处理原始空间中的非线性问题。
• 支持向量
  • 距离超平面最近的一些训练样本点

Adaboost

• 大概流程：（十三）通俗易懂理解——Adaboost算法原理 - 知乎 (zhihu.com)
  • 初始化权重：训练数据中的每个样本最初被赋予相同的权重。
  • 迭代训练：在每一轮中，训练一个弱分类器。
    • 选择误差率最小的分类器作为当前弱分类器
    • 计算当前弱分类器的误差率，更新其权重
    • 对于每个弱分类器，训练集的分布会根据上一轮的错误进行调整，错误分类的样本在下一轮会得到更高的权重
• 隐空间线性，实际是非线性算法
• 总体思想：
  • 数据：训练时加大对错误分类样本的权值
  • 组合分类器：加大误差率小的弱分类器权值

聚类

• 如何定义两个样本是否相似
  • 距离：曼哈顿、欧式、切比雪夫（同KNN），距离越小越相似
  • 相关系数：相关系数越大越相似
  • 夹角余弦：越接近1越相似
• 单个类
  • 定义：集合G中的任意两个样本之间的距离：d<=T ，(T为给定的正数)
  • 特征
    • 类中心（是一个样本，用其代表这个类）：类的均值（类中所有样本均值）
    • 类的直径：类中任意两个样本之间的最大距离
• 类与类的距离
  • 最短距离（单连接）
  • 最长距离（完全连接）
  • 中心距离：各个类的类中心的距离
• 层次聚类
  • 自下而上（聚合聚类）：开始将每个样本各自分到一个类，之后将相距最近（类间距离取最短距离（单连接 ））的两类合并，建立一个新的类，重复操作，直到最后归为一个类
  • 自上而下（分类聚类）：开始将所有样本分到一个类，之后将已有类中相距最远的样本分到两个新的类，重复操作，直到最后各自为一个类
  • 书本例题：关键：合并后的新类的 与其他类的距离值 更新为 最短距离
• K-means聚类
  • 大致流程：
    • 首先选择K个类中心，将各个样本逐个归类到与其最近的（欧式距离的平方）类中心所在的类
    • 更新每个类的样本的均值，作为类的新的中心
    • 直至类中心不变化
    • 详见书本例题
• 对比：
  • 层次聚类：不用定义K，但对大样本计算效率低
  • K>-means：用定义K，对大样本计算效率高，对初始聚类中心的选择敏感，这可能导致算法陷入局部最优解
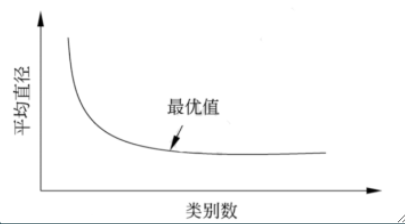
• K的选择
  • 

风险

• 期望风险：模型在整个数据分布上的平均损失 （train+test），理想值，无法直接计算
• 经验风险：train
• 结构风险：经验风险 + 正则化项
• 泛化风险：test

PCA

• 定义：利用正交变换把由线性相关变量表示的观测数据转为少数几个由线性无关变量表示的数据。第一主成分选择方差最大的方向（横向距离最长）
• 作用：降维、用于（高维）数据可视化
• 与特征选择的不同
  • 降维：通过创建新的特征来表示原始特征的组合或转换，可能导致原始特征的一些信息丢失
  • 特征选择：通过筛选出最有用的特征，去掉冗余或无关的特征，保持原始特征不变
• 维度灾难
  • 影响：高维空间中，基于距离的算法受到影响，因为数据点之间的距离变得不那么区分明显，使得算法难以有效区分不同的数据点或者识别出相似的数据点。
• 步骤
  • 标准化数据：使得每个特征均值为0、方差为1
  • 计算协方差矩阵：反映了特征之间的相关性。
  • 特征值分解：计算协方差矩阵的特征值和特征向量。
  • 选择主成分：根据特征值大小排序，最大的作为最重要的成分，将样本点投影到选取的特征向量上

深度学习

• 激活函数的作用：让某些神经元激活，让某些神经元不激活，构成非线性的网络，引入非线性性质，使得神经网络能够学习和表示更复杂的函数关系
• sigmoid：将输入压缩到0和1之间。
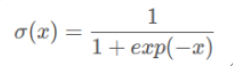
  • 作用：使得输出的概率向量中最大的类概率变得更大（小的变得更小）
  • 问题：
    • 对于远离0的输入，梯度很小，可能导致梯度消失问题。
    • 不是零中心化的，可能导致优化过程中的收敛速度减慢。
• 其他激活函数：ReLU（负输入为0，正输入为本身）、Tanh（-1到1）

范数计算

• L1：绝对值相加
• L2：平方相加再开根（向量长度）
• L无穷范：取分量绝对值最大

梯度下降与随机梯度下降SGD

• 梯度下降：在每次迭代中，它会计算所有训练样本的损失函数的梯度，并根据这个梯度更新参数。这意味着每一步更新都考虑了所有的训练数据。计算非常耗时
• 随机梯度下降：每次更新只使用一个训练样本来计算梯度。计算效率高，但收敛可能不稳定（随机）

线性回归

• 似然估计推导均方误差（推导很重要）
• 求解参数（推导很重要）
  • 最小二乘法的闭合求解（一元、多元）
  • 梯度下降
• 岭回归：
• Lasso回归：

逻辑回归

• 与线性回归的区别：非线性、分类
• 似然估计推导交叉熵（推导很重要）
• 梯度下降求解参数（推导很重要）
• Sigmoid在逻辑回归中的作用
  • 将线性模型的输出转换为概率估计，适用于二分类问题
  • Sigmoid函数的导数形式简单，便于进行梯度下降等优化算法

最大熵模型

• 学习概率模型时，在所有可能的概率模型(分布)中，熵最大的模型是最好的模型，表述为在满足约束条件的模型集合中选取熵最大的模型，最大熵模型由最大熵原理推导实现。
• 最大熵关注于在不确定性下选择一个最合理的模型，在最大化熵的过程中，我们试图找到最不偏不倚的模型。假设有一个六面的骰子，我们没有任何关于其偏重的信息。最大熵原理告诉我们，最合理的假设是每个面出现的概率都是相等的（1/6），因为这个概率分布的熵是最大的，即最不确定，没有任何面被偏爱。

适用性讨论

• 感知机：少样本、低维、线性、二分类
• KNN：少样本、低维、分类与回归（非线性）
• 朴素贝叶斯：中大样本、高维表现优秀
• 决策树：中大样本（可能过拟合）、高维（树复杂）、分类与回归、（非线性）
• 支持向量机：小中样本、高维表现优秀、分类与回归、（可线性可非线性）
• K-means：大样本、低维（高维中距离计算效果不好）
• 层次聚类：小样本、低维
• 集成学习：（非线性）