Tarjan算法（详解 + 刷题）

目录

🎂前言

💪无向图的桥（割边）

解释

图解

代码?

v == fa 要 continue 的解释

💪无向图的割点

图解?

代码

🌼有向图 -- 强连通分量

图解

代码

?刷题

🌳电话网络

🌳道路建设

?计划有变

🌳图的底部

🌳校园网络

---

🎂前言

学完 tarjan 算法后，说下我对割边（桥）和割点的理解，大家可以对照图解，自行理解

对于无向图的割边，我的理解是，如果low[v] > dfs[u]，说明 起点?u 和 终点 v 之间不能形成环（因为一旦形成环，low[v] 就会被更新成 <= dfs[u] 的值），所以当砍掉 u -- v 这条边，图就会形成两部分

而对于割点的理解，先讨论非根节点的情况，如果 low[v] <= dfs[u]，< 时说明 u, v两点不是环的一部分，= 说明，有环，但是是环的起点

时间戳(depth first number)：dfn[u]，节点 u 深度遍历的序号（即节点被访问的先后顺序）

追溯点(low point)：low[u]，节点 或 子节点，能追溯到的最小时间戳（回到最早的过去）

注意！这里的追溯，必须通过非父子边，也就是不能原路返回，只能往前走，到达以前走过的点

💪无向图的桥（割边）

解释

tarjan() 函数实现了 Tarjan算法中的桥的查找

对于每个节点 u，它的深度优先搜索编号 dfn[u] 和追溯点 low[u] 都被初始化为 num+1，表示已经访问过一个新的节点

每个邻居节点 v，如果它没有被访问过，就递归调用 tarjan 函数来处理节点 v，并更新当前节点 u 的追溯点 low[u]

如果更新后 v 的追溯点值 low[v] 大于 u 的顺序编号 dfn[u]，说明边 (u,v) 是桥，输出结果

图解

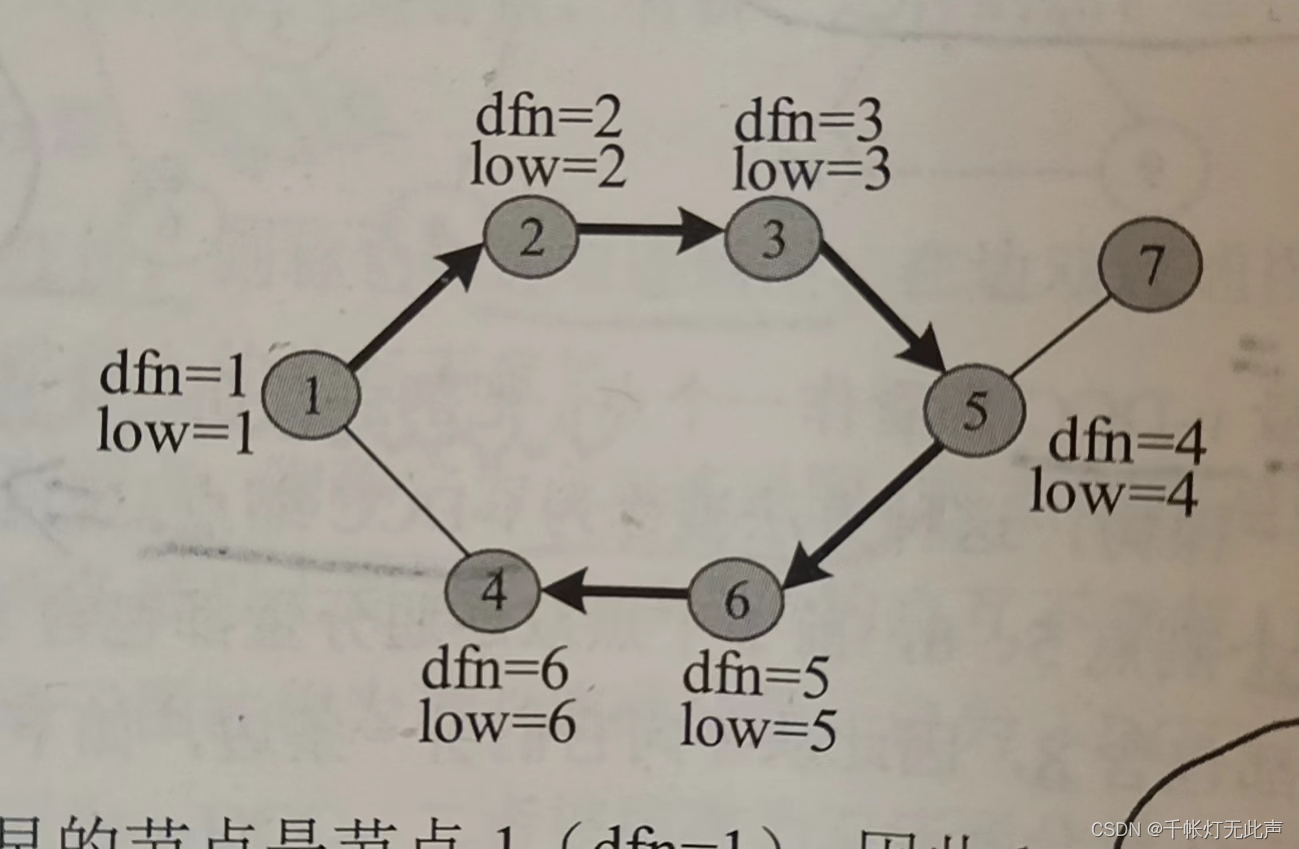
初始化

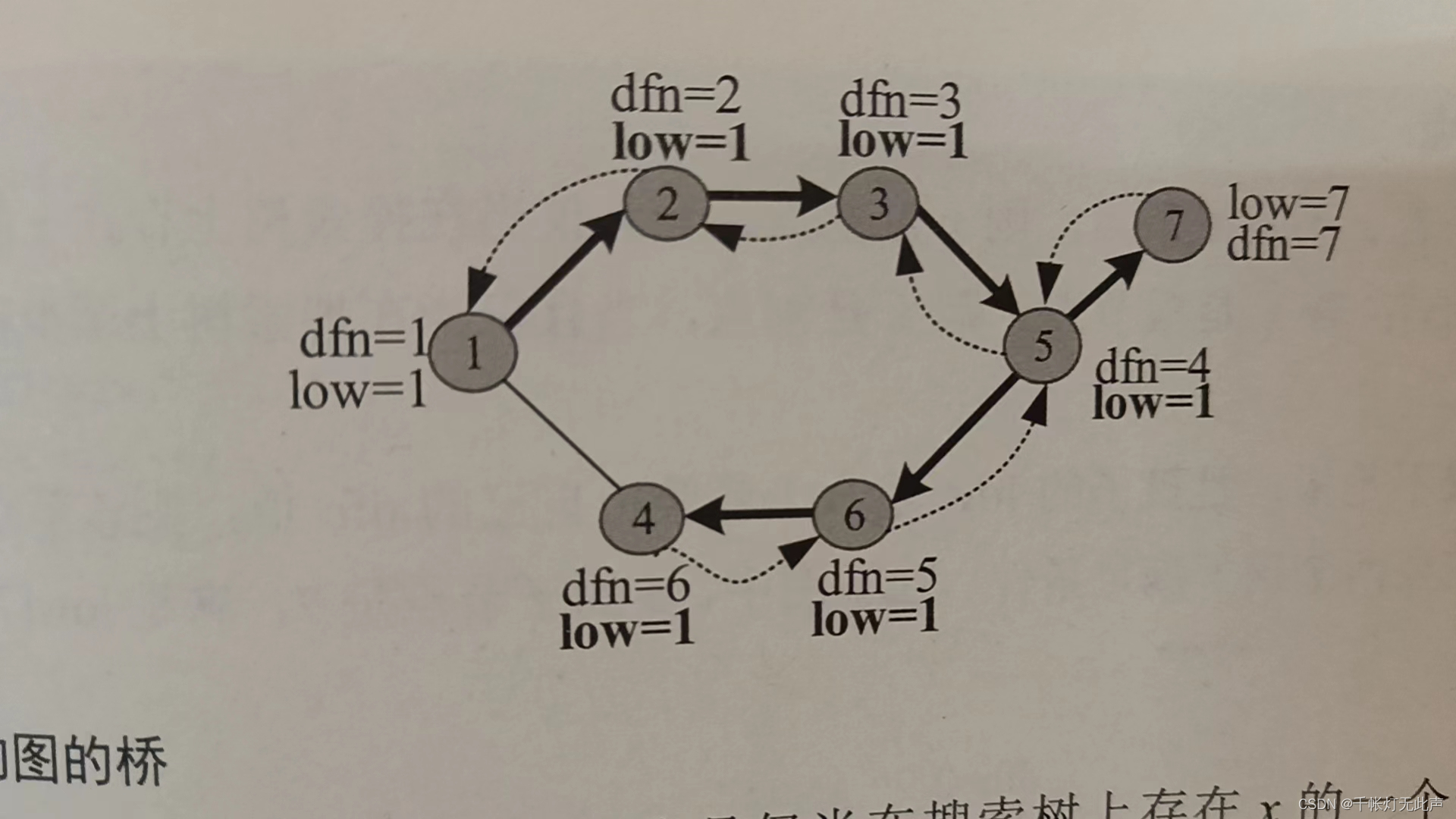
查找桥

low[7] == 7 > dfn[5] == 4

解释下，通过非父子边，如何追溯到最小时间戳

low[u] = min(low[u], low[v]);
// u 是父节点, v 是子节点
// u --> v  表示 父节点 到 子节点
// 初始化时, low[v] = low[u] + 1
// 当 v 为已访问
// low[u] = min(low[u], dfn[v]);
// 同时回溯到之前走过的父节点
// 并通过 low[u] = min(low[u], low[v]) 这一行更新父节点

代码?

#include <iostream>
#include <algorithm>
using namespace std;

const int MAXN = 1005;
const int MAXM = 10005;

struct Edge {
    int to; // 边的终点
    // 链式前向星中指向下一条边的指针，实际是上一条边的编号
    int next; 
} e[MAXM];

int head[MAXN]; 
int dfn[MAXN]; // dfs编号
int low[MAXN]; // 追溯点
int num = 0; // 当前节点

// 添加无向边
void addEdge(int u, int v) {
    static int idx = 0; // 静态变量，用来记录边的编号
    e[++idx] = {v, head[u]};
    head[u] = idx; // 节点 u 为起点的第一条边编号
}

// Tarjan算法查找桥
void tarjan(int u, int fa) {
    dfn[u] = low[u] = ++num; // 初始化为num+1，表示已访问
    for (int i = head[u]; i; i = e[i].next) { // 遍历 u 所有邻接点
        int v = e[i].to; // 边的终点
        if (v == fa) continue;
        if (!dfn[v]) { // v 未访问
            tarjan(v, u); // 处理下一节点
            low[u] = min(low[u], low[v]); // 更新追溯值low[u]
            if (low[v] > dfn[u]) // 边(u,v)是桥
                cout << u << "——" << v << "是桥" << endl; // 输出结果
        }
        else // 如果v已经被访问过
            low[u] = min(low[u], dfn[v]); // 更新当前节点u的追溯点值low[u]
    }
}

int main() {
    int n, m;
    cin >> n >> m; // 节点数和边数
    for (int i = 1; i <= m; i++) { // m条边, 构建邻接表
        int u, v;
        cin >> u >> v;
        addEdge(u, v);
        addEdge(v, u); // 无向图
    }

    tarjan(1, -1); // 从节点1开始遍历整个图

    return 0;
}

7 7
1 2
2 3
3 5
5 6
6 4
4 1
5 7
5——7是桥

v == fa 要 continue 的解释

解释一下，为什么 v == fa，要 continue

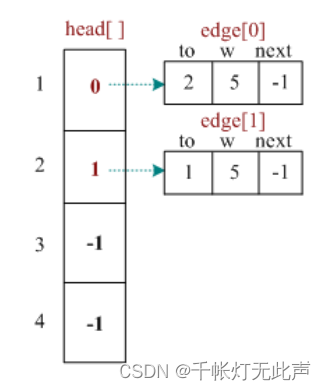
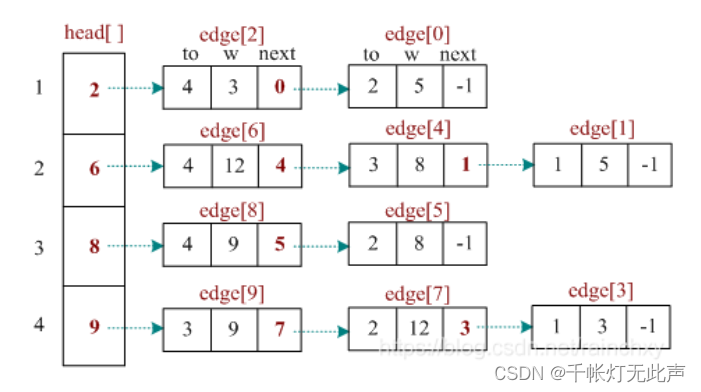
if (v == fa) continue;

这里需要结合链式前向星的结构，它采用头插法

链式前向星——最完美图解-腾讯云开发者社区-腾讯云 (tencent.com)

结构体中 to 表示 当前边的 终点，next 表示上一条边

又因为 head[i] 表示 节点 i 的第 1 条边编号

举个例子👇

输入 1 2 5....这里head[1] == 0，表示节点 1 第 1 条边是 0 号边，即 1 -- 2

输入 2 1 5....这里head[2] == 1，表示节点 2 第 1 条边是 1 号边，即 2 -- 1

输入1 4 3后，会插到中间。

这里? head[1] == 2 表示节点 1 第 1 条边是 2 号边，即 1 -- 4?

图中 edge[0].next == -1，表示 0 号边没有上一条边

edge[2].next == 0，表示 2 号边上一条边是 0 号

最后该无向图得到的链式前向星👇

它存储的是，以每一条边为起点的，边的集合

而代码中

void tarjan(int u, int fa) {
    ...
    for (int i = head[u]; i; i = e[i].next) {
        ...
        int v = e[i].to
        if (v == fa) continue;
        ...
    }
}

fa 为起点, u 为终点, 此时 for 循环，遍历终点 u 的所有邻接点

i 为这些邻接点的第 1 条边，e[i].to 则表示终点 u 的邻接点

当终点?u 的邻接点 v == 起点 fa

举个例子👇

起点 1，终点 2，for 循环遍历终点 2 的所有邻接点，2 -- 1, 2 -- 5, 2 -- 6

然后现在是深度优先遍历，往后走是没有意义的，所以 2 -- 1 要 continue

💪无向图的割点

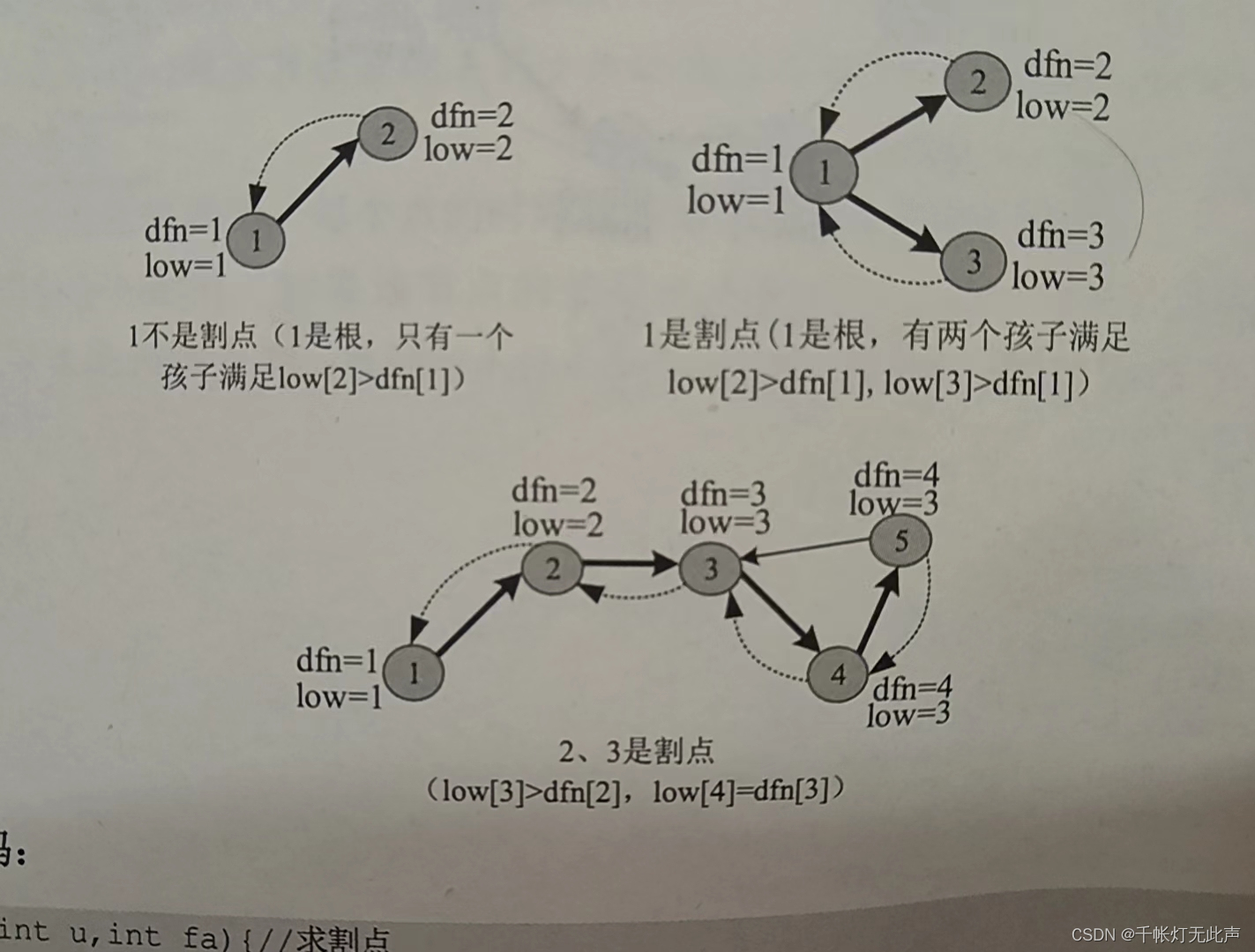
图解?

解释

在一张无向图中，如果去掉一个顶点（以及与该顶点相关联的边）后，原来的图被分成了两个或以上的连通块，则该顶点被称为这张图的割点

换言之，割点是指如果该点被移除，图会变成不连通的点

简单来说，割点就是将一个图划分成了多个不相交部分的顶点

几种割点判定情况

dfn[5] 应该是 dfn = 5 才对，打印错了

代码

void tarjan(int u, int fa) {
    dfn[u] = low[u] = ++num;  // 初始化dfn和low值为当前时间戳
    int count = 0;  // 记录子节点数量
    for (int i = head[u]; i; i = e[i].next) {  // 遍历以u为起点的边
        int v = e[i].to;  // 获取当前边的终点
        if (v == fa) continue;  // 终点的邻接点是起点，跳过
        if (!dfn[v]) {  // 如果终点未被访问
            tarjan(v, u);  // 递归处理终点
            low[u] = min(low[u], low[v]);  // 更新u的low值
            if (low[u] >= dfn[v]) {  // 判断是否是割点
                count++;  // 增加子节点数量
                if (u != root || count > 1)  // 如果不是根节点或者有多个子节点
                    cout << u << "是割点" << endl;  // 输出割点信息
            }
        }
        else 
            low[u] = min(low[u], dfn[v]);  // 更新u的low值
    }
}

🌼有向图 -- 强连通分量

强连通分量（超详细！！！） - endl\n - 博客园 (cnblogs.com)

其实连通分量，就是一个整体，看互相之间能不能到达（对于整体中任意两个点都成立）

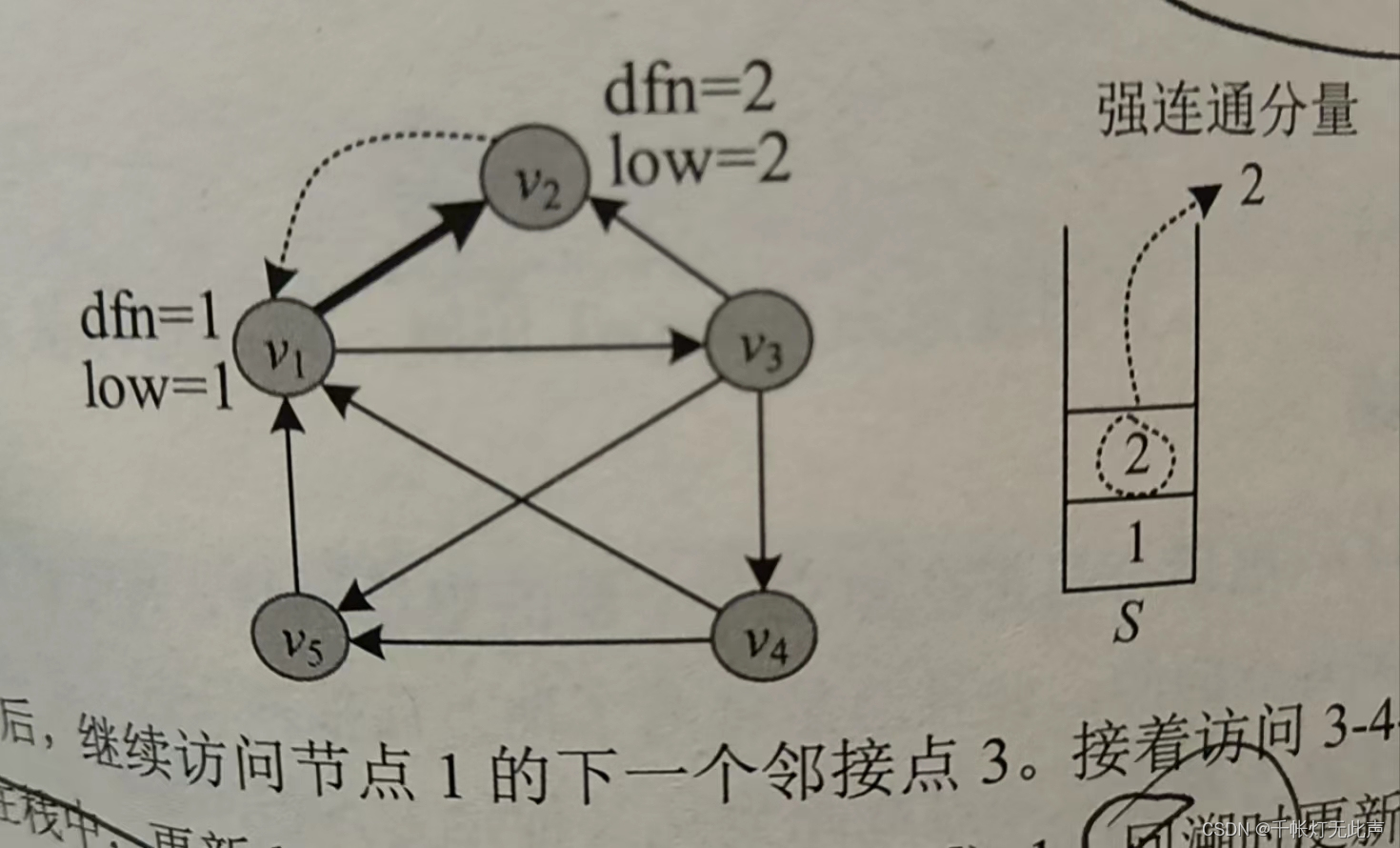
图解

v2 单个元素，作为一个整体，就是一个强连通分量👇

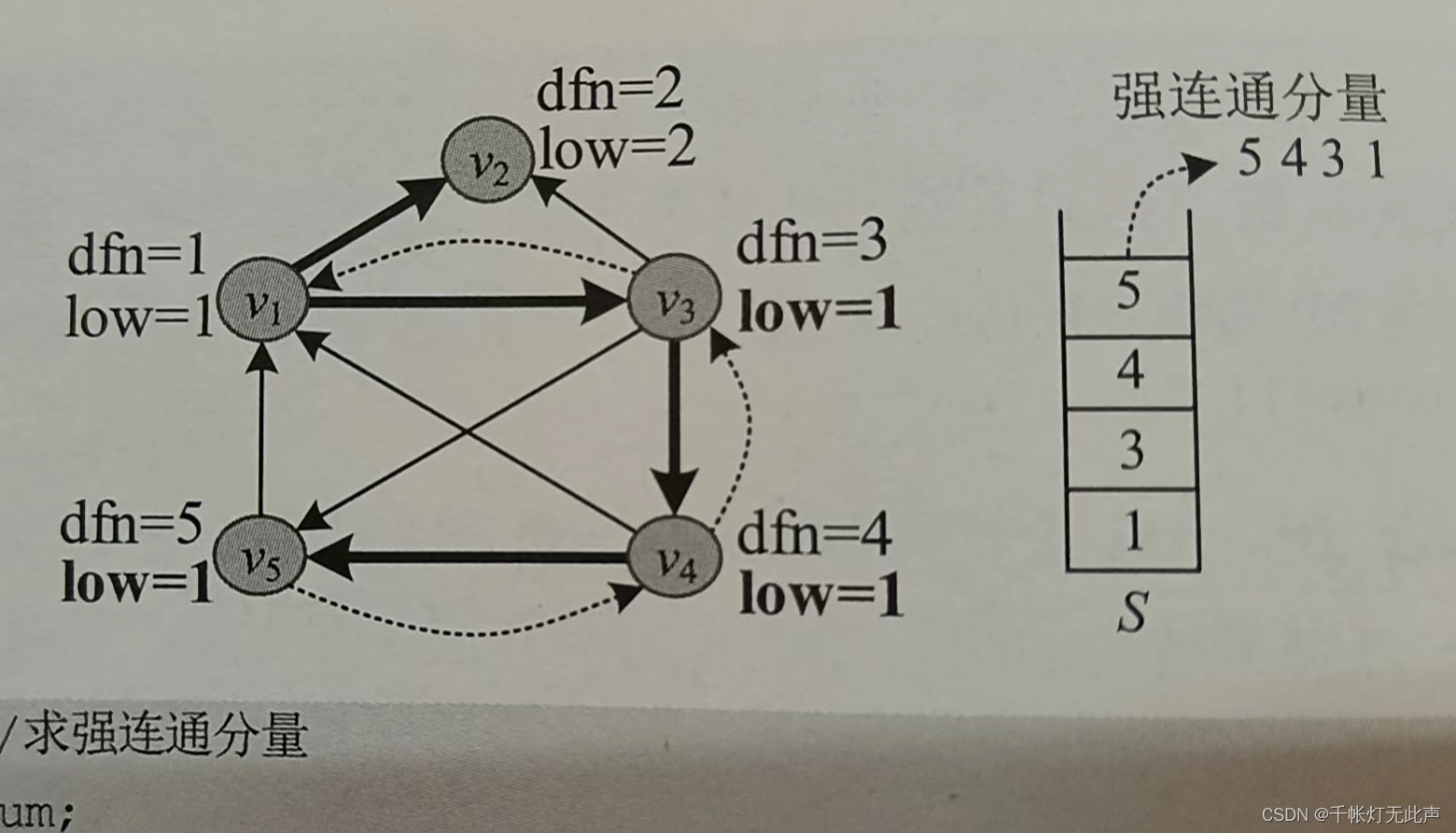
v5，v4，v3，v1 的整体，作为一个强连通分量👇

代码

#include <iostream>
#include <stack>
using namespace std;

const int MAXN = 1000; // 最大顶点数
struct Edge {
    int to, next;
} e[MAXN];
int head[MAXN], dfn[MAXN], low[MAXN], num; // dfn[] 访问顺序，low[] 能追溯到的最小序列号
bool ins[MAXN]; // 标记在栈中(ins -- in stack)
stack<int> s;

void tarjan(int u)
{
    low[u] = dfn[u] = ++num; // 初始化
    ins[u] = true; // 标记 u 在栈里
    s.push(u); // u 入栈

    // 遍历 u 所有出边
    for (int i = head[u]; i; i = e[i].next) {
        int v = e[i].to; // 边终点  u -- v

        if (!dfn[v]) { // v 未访问
            tarjan(v); // 递归访问 v
            low[u] = min(low[u], low[v]); // 更新 u 的最小序列号
        }
        else if (ins[v]) { // v 已访问
            low[u] = min(low[u], dfn[v]); // u, v 同一强连通分量, 更新为下步回溯准备
        }
    }

    if (low[u] == dfn[u]) { // 当前节点 u 是该强连通分量根节点
        int v;
        cout << "强连通分量：";
        do {
            v = s.top(); // 取顶点 v
            s.pop(); 
            cout << v << " "; // 输出顶点v
            ins[v] = false; // 将顶点v标记为不在栈中
        } while (v != u); // 循环直到取出的顶点v为顶点u，即输出完整的强连通分量
        cout << endl;
    }
}

?刷题

🌳电话网络

1144 -- Network (poj.org)

翻译

They are connecting several places numbered by integers from 1 to N

节点从 1 ~ N

The lines are bidirectional

线路是双向的

From time to time the power supply fails at a place and then the exchange does not operate. The officials from TLC realized that in such a case it can happen that besides the fact that the place with the failure is unreachable, this can also cause that some other places cannot connect to each other.

求无向图割点数

The input file consists of several blocks of lines. Each block describes one network.

多个测试用例?

Each of the next at most N lines contains the number of a place followed by the numbers of some places to which there is a direct line from this place.

每一行第一个地点编号后的数字，是它可以直达的所有点

Each block ends with a line containing just 0. The last block has only one line with N = 0

每个测试用例，用单独一行 0 结束。N = 0 时输入结束，不处理?

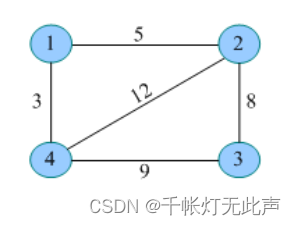
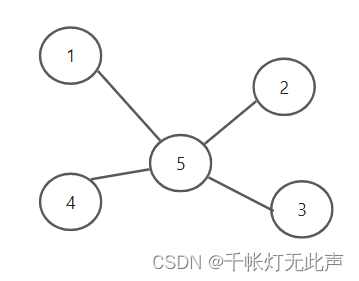
样例图解

5

5 1 2 3 4

0

6

2 1 3

5 4 6 2

0

AC? 代码

用 G++ 提交

tarjan() 也可以只有一个参数 u，那么就少了，if (v == fa) continue; 的判断

#include<iostream>
#include<cmath>
#include<cstring>
#include<cstdio> // getchar()
using namespace std;

const int N = 110;
struct edge
{
    int to; // 边终点
    int next; // 上一条边编号
}e[N*N]; // 边集数组是 N*N

int head[N]; // 当前点的第1条边
int dfn[N]; // 遍历顺序
int low[N]; // 追溯点
int num = 0, cnt = 0; // 当前节点编号 和 边的编号
int dot[N]; // 割点
int root; // 根节点

// 添加无向边
void addEdge(int u, int v) // 起点 u, 终点 v
{
    e[++cnt] = {v, head[u]}; // 初始没有上一条边, 所以head[u] == 0
    head[u] = cnt;
}

// tarjan() 判断割点
// fa 起点, u 终点
void tarjan(int u, int fa)
{
    int count = 0;

    dfn[u] = low[u] = ++num; // 初始化
    // 遍历终点 u 所有邻接点
    for (int i = head[u]; i; i = e[i].next) { // i 为邻接点第1条边
        int v = e[i].to; // u 的邻接点

        if (v == fa) continue; // dfs 不需要往回走

        if (!dfn[v]) { // 邻接点 v 未访问
            tarjan(v, u); // 递归
            low[u] = min(low[u], low[v]); // 回溯

            // 判断割点
            if (low[v] >= dfn[u]) {
                count++;
                if (count >= 2 || u != root)
                    dot[u] = 1; // 节点 u 是割点
            }
        }
        else 
            low[u] = min(low[u], dfn[v]); // 有环就更新
    }
}

void init()
{
    memset(head, 0, sizeof(head));
    memset(dfn, 0, sizeof(dfn));
    memset(low, 0, sizeof(low));
    memset(dot, 0, sizeof(dot));
    cnt = num = 0;
}

int main()
{
    int n;
    while (cin >> n && n) {
        init(); // 每组测试数据都要初始化
        int u, v;
        while (cin >> u && u) { // 输入第一个节点
            while (1) {
                char c = getchar(); // 读取' '或'\n'
                if (c == '\n') break; // 跳出这一行
                cin >> v;
                addEdge(u, v); addEdge(v, u); // 无向边
            }
        }
        // 遍历每个点, 确保找到所有连通分量
        for (int i = 1; i <= n; ++i)
            if (!dfn[i]) {
                root = i;
                tarjan(i, -1); // 从根节点 i 开始
            }
        int ans = 0;
        for (int i = 1; i <= n; ++i)
            if (dot[i]) ans++;
        cout << ans << endl;
    }
    return 0;
}

🌳道路建设

?计划有变

考虑到大二暑期实习的迫切性，调整策略，《算法训练营入门篇》，每个算法做 1 ~ 2 题

而不是每次做完 4 ~ 5 题

以后如果有时间，需要去了解相关算法，再回来复习和刷题

3352 -- Road Construction (poj.org)

🌳图的底部

2553 -- The Bottom of a Graph (poj.org)

🌳校园网络

1236 -- Network of Schools (poj.org)