【BBuf的CUDA笔记】十二，LayerNorm/RMSNorm的重计算实现

带注释版本的实现被写到了这里：https://github.com/BBuf/how-to-optim-algorithm-in-cuda/tree/master/apex 由于有很多个人理解，读者可配合当前文章谨慎理解。

0x0. 背景

我也是偶然在知乎的一个问题下看到这个问题，大概就是说在使用apex的LayerNorm/RMSNorm的时候可以打开这个api的memory_efficient开关，这个开关可以在速度和精度无损的情况下节省网络训练的显存占用。感觉比较有趣，我就研究了一下，因此也就有了这篇文章。

我去实测了一下，单机8卡A100训练LLama7B，纯数据并行的情况下打开memory_efficient开关相比于不打开节省了大约2个G的显存，如果模型继续scale up，那么省掉的显存也会更多。因此，本文就是对这个memory_efficient开关的背后实现做一个解读，另外也会对apex里面LayerNorm/RMSNorm本身的cuda kernel实现做一个细节解读。

apex的LayerNorm/RMSNorm被实现成一个fuse kernel，然后上层使用torch.autograd.Function来封装，本文的讲解主要以LayerNorm为例子，入口见：https://github.com/NVIDIA/apex/blob/master/apex/normalization/fused_layer_norm.py#L32-L51 。实际上RMSNorm和LayerNorm的实现是共享的，只不过在kernel内部会区分一下缩放策略是2个参数（LayerNorm的gamma和beta）还是一个参数。

class FusedLayerNormAffineFunction(torch.autograd.Function):
    @staticmethod
    def forward(ctx, input, weight, bias, normalized_shape, eps, memory_efficient=False):
        global fused_layer_norm_cuda
        if fused_layer_norm_cuda is None:
            fused_layer_norm_cuda = importlib.import_module("fused_layer_norm_cuda")
        ctx.normalized_shape = normalized_shape
        ctx.eps = eps
        ctx.memory_efficient = memory_efficient
        input_ = input.contiguous()
        weight_ = weight.contiguous()
        bias_ = bias.contiguous()
        output, mean, invvar = fused_layer_norm_cuda.forward_affine(
            input_, ctx.normalized_shape, weight_, bias_, ctx.eps
        )
        if ctx.memory_efficient:
            ctx.save_for_backward(output, weight_, bias_, None, invvar)
        else:
            ctx.save_for_backward(input_, weight_, bias_, mean, invvar)
        return output

可以看到在非memory_efficient模式下面，ctx.save_for_backward(output, weight_, bias_, None, invvar)保存了用于backward的tensor，包括输入，权重，偏置，均值和方差的逆。但在memory_efficient模式下面ctx.save_for_backward(output, weight_, bias_, None, invvar)，则是保存了输出，权重偏置以及方差的逆。

这个地方看下你是否会掉入误区？从表面上看，这里也就只省掉了一个gamma，因为输入和输出tensor的形状是一样的，那么这样还有什么收益呢？背景是，在pre-ln的transformer架构里面LayerNorm/RMSNorm之后紧接着是一个线性投影，无论是在注意力机制还是在多层感知机（mlp）中都是如此，所以输出Tensor一定要被保存下来。而在post-ln架构中，输出还会直接用于残差连接。然而，在这两种情况下，LayerNorm/RMSNorm的输入都不再被使用，所以这里原本的输入保存变得相当多余，因为我们可以保存无论如何都会被保存的输出张量。这样就可以达到节省显存的目的了。

接下来就详细解读下实现。

0x1. Apex的LayerNorm前向cuda实现

https://github.com/NVIDIA/apex/blob/master/csrc/layer_norm_cuda.cpp 这个文件是基于实现的LayerNorm cuda kernel使用torch extension模块导出python接口。

同时这个文件还写了几个工具函数，比如compute_n1_n2用来计算LayerNorm中非归一化和归一化部分的大小：https://github.com/BBuf/how-to-optim-algorithm-in-cuda/blob/master/apex/layer_norm_cuda.cpp#L7C31-L7C51 ，check_args函数对LayerNorm的参数进行检查：https://github.com/BBuf/how-to-optim-algorithm-in-cuda/blob/master/apex/layer_norm_cuda.cpp#L32C22-L143 。

此外，这个cpp预定义了cuda_layer_norm的函数接口，并且考虑了gamma/beta是否为空。

接下来就正式对LayerNorm的前向cuda实现进行解析。

0x1.1 工具函数

LayerNorm使用Welford算法统计均值方差，在 https://github.com/NVIDIA/apex/blob/master/csrc/layer_norm_cuda_kernel.cu 写了一系列kernel实现中需要用到的工具函数，这些函数是gpu上用到的。下面对其简单解析一下，另外Welford算法可以看这篇博客的介绍：用Welford算法实现LN的方差更新（感叹一下，zzk写这篇文章的时候还是萌新，经过2年时间已经成长为国内顶级的工程师了，开挂般学习能力） 。工具函数包含：cuWelfordOnlineSum，cuChanOnlineSum，cuRMSOnlineSum，cuChanRMSOnlineSum这些，我把自己的原始注释使用gpt4进行了润色，这样会显得更加通俗一些。具体解释如下：

// 这段代码是个CUDA函数，名叫cuWelfordOnlineSum，擅长用Welford算法来边收数据边算这些数据的平均值和变化范围（就是均值和方差）。
// 用Welford算法来算这个，特别稳，不会因为数据太多而出错，而且每加一个数据就能更新一次均值和方差。
// const U curr: 这个是新来的数据点。
// U& mu: 这个是我们到现在为止算出来的所有数据的平均值。
// U& sigma2: 这个是我们到现在为止算出来的方差，可以告诉你数据变化有多大。
// U& count: 这个记录了我们到现在处理了多少数据点。

template<typename U> __device__
void cuWelfordOnlineSum(
  const U curr,
  U& mu,
  U& sigma2,
  U& count)
{
  count = count + U(1); // 每次调用这个函数，就把处理的数据数量加一。
  U delta = curr - mu; // 看看新数据和现有平均值差多少。
  U lmean = mu + delta / count; // 用这个差值和数据总量来算一个新的平均值。
  mu = lmean; // 把这个新算的平均值记下来。
  U delta2 = curr - lmean; // 现在再算一下新数据和新平均值的差。
  sigma2 = sigma2 + delta * delta2; // 利用这个新旧平均值的差来更新方差。
}

// 这段代码是个CUDA函数，名叫cuChanOnlineSum。它用于处理一种特殊的情况：
// 当你有两堆数据，想要快速算出它们合并后的平均值和方差时，这个函数就派上用场了。
// const U muB, sigma2B, countB: 这三个是你新加入的那堆数据的平均值、方差和数据点数量。
// U& mu, sigma2, count: 这三个是你之前已经有的数据的平均值、方差和数据点数量。
// 这个函数会更新这些值，让它们反映出两堆数据合并后的情况。

template<typename U> __device__
void cuChanOnlineSum(
  const U muB,
  const U sigma2B,
  const U countB,
  U& mu,
  U& sigma2,
  U& count)
{
  U delta = muB - mu; // 先算算新数据堆和老数据堆的平均值差了多少。
  U nA = count; // 记下当前数据堆（我们叫它A堆）的大小。
  U nB = countB; // 看看新来的那堆数据（B堆）有多少个点。
  count = count + countB; // 把两堆数据的数量加起来。
  U nX = count; // 这就是合并后总数据量的大小。
  if (nX > U(0)) {
    nA = nA / nX; // 算一下A堆数据在总数据中占的比例。
    nB = nB / nX; // 同理，算一下B堆的比例。
    mu = nA*mu + nB*muB; // 利用这些比例和各自的平均值，算出总的平均值。
    sigma2 = sigma2 + sigma2B + delta * delta * nA * nB * nX; // 然后用一点复杂的公式，把方差也算出来，这个公式考虑了两堆数据的方差和它们平均值的差异。
  } else {
    // 如果合并后的总数是0，那就说明两堆数据其实都是空的，所以把平均值和方差都设为0。
    mu = U(0);
    sigma2 = U(0);
  }
}

// 这里定义了一个名叫cuRMSOnlineSum的CUDA函数，它的主要任务就是在线实时计算一串数据的平方和。
// 你可能会问，为什么要算平方和呢？这是因为我们可以用它来算出均方根（RMS, Root Mean Square），
// 均方根是一种描述数据波动大小的指标，特别常用于信号处理领域。
template<typename U> __device__
void cuRMSOnlineSum(
  const U curr,
  U& sigma2)
{
  sigma2 = sigma2 + curr * curr; // 每次函数被调用，就把当前值的平方加到累计平方和中。
}

// 又定义了一个名叫cuChanRMSOnlineSum的CUDA函数，这个家伙的工作就是帮你算两组数据的平方和总和。
// 当你有两组数据，想要快速合并它们的均方根（RMS）时，这个函数就能派上用场。
// 它其实是均方根计算过程中的一个环节，用于处理两个独立数据集的情况。
template<typename U> __device__
void cuChanRMSOnlineSum(
  const U sigma2B,
  U& sigma2)
{
  sigma2 = sigma2 + sigma2B; // 这里就简单直接了，把第二组数据的平方和加到当前的累计值上。
}	

这里还有一个函数cuWelfordMuSigma2是用来计算张量某一维度上的均值（mu）和方差（sigma2）的，它调用了上面的工具函数，但是这个函数我们在kernel实现阶段解析，因为它需要一些kernel启动的背景。

0x1.2 启动逻辑

先对kernel启动这部分的代码进行注释，首先是共享内存的结构体定义。

// 这段代码定义了一个叫做SharedMemory的模板结构体，专门用在CUDA设备函数里来访问所谓的“共享内存”。
// 在CUDA编程里，共享内存是一种特别高效的内存类型，非常适合用来在CUDA的一个块（block）内的不同线程间共享数据。
// 这里还包括了针对float和double类型数据的SharedMemory结构体的特化版本。

namespace {
// 这是通用的SharedMemory结构体模板。注意，我们通过在函数体内使用一个未定义的符号来阻止这个结构体被实例化，
// 这样如果尝试用未特化的类型来编译这个结构体，编译器就会报错。
// template <typename T>
// struct SharedMemory
// {
//     // 确保我们不会编译任何未特化的类型
//     __device__ T *getPointer()
//     {
//         extern __device__ void error(void);
//         error();
//         return NULL;
//     }
// };

template <typename T>
struct SharedMemory;

// 这是SharedMemory结构体针对float类型的特化版本。
template <>
struct SharedMemory <float>
{
    // 这个函数返回一个指向共享内存的float类型指针。
    __device__ float *getPointer()
    { 
        // 这里声明了一个名为s_float的外部共享内存数组，用于存储float类型的数据。
        // extern和__shared__关键字表明这个数组是在共享内存中定义的。
        extern __shared__ float s_float[];
        return s_float;
    }
};

// 下面是针对double类型的特化版本，工作方式和float版本相似。
template <>
struct SharedMemory <double>
{
    __device__ double *getPointer()
    {
        extern __shared__ double s_double[];
        return s_double;
    }
};
}

然后是Kernel启动的具体逻辑部分：

// 这段代码里，我们定义了一个CUDA设备函数叫做cuApplyLayerNorm_，它的主要任务是执行LayerNorm（层归一化）。
// 层归一化是深度学习中的一个技巧，用来让每一层的输出更加标准化，有助于模型训练。
// 我们定义了三种模板参数：T是输入数据类型，U是中间计算（比如均值和方差）的类型，V是输出数据类型。
// output_vals, mean, invvar, vals, gamma, beta 这些都是指向不同数据的指针。
// 在层归一化中，我们通常把一个多维数据（张量）分为两部分：一部分用来做标准化，另一部分保持原样。
// 比如，如果你有一个 [batch_size, channels, height, width] 形状的4D张量，
// 而你只想对最后两个维度进行层归一化，那么n1是batch_size * channels，n2是height * width。
template<typename T, typename U, typename V> __device__
void cuApplyLayerNorm_(
  V* __restrict__ output_vals,
  U* __restrict__ mean,
  U* __restrict__ invvar,
  const T* __restrict__ vals,
  const int n1,
  const int n2,
  const U epsilon,
  const V* __restrict__ gamma,
  const V* __restrict__ beta,
  bool rms_only
  )
{
  // 基本假设：
  // 1) blockDim.x 是 warp 的大小（这是一个CUDA的技术细节）。
  // 2) 输入的张量数据在内存中是连续的。
  //
  // 这段代码遍历n1维度，每次处理一个i1索引。
  // 假设每个CUDA线程块的x维度等于warp大小，确保数据处理是高效的。
  // 这里一个线程可能要处理多行，所以我们用gridDim.y来控制步长。（因为gridDim.x=1）
  for (auto i1=blockIdx.y; i1 < n1; i1 += gridDim.y) {
    SharedMemory<U> shared;
    U* buf = shared.getPointer(); // 创建一个 SharedMemory 实例用于处理类型 U 的数据。
    U mu,sigma2; // 这里mu和sigma2分别代表均值和方差，我们接下来要计算它们。
    // 调用 cuWelfordMuSigma2 函数计算给定索引 i1 处的均值（mu）和方差（sigma2）。
    cuWelfordMuSigma2(vals,n1,n2,i1,mu,sigma2,buf,rms_only);

    // 定位到当前 i1 索引处的输入和输出的起始位置。
    const T* lvals = vals + i1*n2;
    V* ovals = output_vals + i1*n2;
    // 计算逆方差 c_invvar，这是层归一化中一个关键的步骤。
    U c_invvar = rsqrt(sigma2 + epsilon);
    // 计算每个 CUDA 块的线程总数 (numx) 和当前线程的一维索引 (thrx)。
    const int numx = blockDim.x * blockDim.y;
    const int thrx = threadIdx.x + threadIdx.y * blockDim.x;
    // 如果提供了gamma和beta参数，或者我们只是在做RMS计算，我们会用一种特别的方式来计算输出值。
    if (gamma != NULL && (beta != NULL || rms_only)) {
      for (int i = thrx;  i < n2;  i+=numx) {
        U curr = static_cast<U>(lvals[i]);
        if (!rms_only) {
          // 标准化当前值，然后用gamma和beta进行调整。
          ovals[i] = gamma[i] * static_cast<V>(c_invvar * (curr - mu)) + beta[i];
        } else {
          // // 如果是RMS模式，我们稍微简化计算过程。
          ovals[i] = gamma[i] * static_cast<V>(c_invvar * curr);
        }

      }
    } 
    // 否则，如果没有提供gamma和beta，我们就直接用计算出的均值和逆方差来进行标准化。
    else {
      for (int i = thrx;  i < n2;  i+=numx) {
        U curr = static_cast<U>(lvals[i]);
        if (!rms_only) {
        	 // 直接进行标准化计算。
          ovals[i] = static_cast<V>(c_invvar * (curr - mu));
        } else {
          // // RMS模式下的简化计算。
          ovals[i] = static_cast<V>(c_invvar * curr);
        }
      }
    }
    // 在每个 CUDA 块中，仅由一个线程（线程 (0,0)）更新均值和逆方差。
    if (threadIdx.x == 0 && threadIdx.y == 0) {
      if (!rms_only) {
        mean[i1] = mu;
      }
      invvar[i1] = c_invvar;
    }
    // 用于同步块内的所有线程。
    __syncthreads();
  }
}

// 对上个函数的参数透传，不过rms_only设为False
template<typename T, typename U, typename V=T> __global__
void cuApplyLayerNorm(
  V* __restrict__ output_vals,
  U* __restrict__ mean,
  U* __restrict__ invvar,
  const T* __restrict__ vals,
  const int n1,
  const int n2,
  const U epsilon,
  const V* __restrict__ gamma,
  const V* __restrict__ beta
  )
{
  cuApplyLayerNorm_<T, U, V>(output_vals, mean, invvar, vals, n1, n2, epsilon, gamma, beta, false);
}

// kernel启动代码，设置线程块和线程数
template<typename T, typename U, typename V=T>
void HostApplyLayerNorm(
    V* output,
    U* mean,
    U* invvar,
    const T* input,
    int n1,
    int n2,
    double epsilon,
    const V* gamma,
    const V* beta
    )
{
    // threads和blocks定义了CUDA内核的线程和块的维度。这里，每个线程块有32×4的线程，而块的数量由n1和GPU设备的最大网格大小限制决定。
    auto stream = at::cuda::getCurrentCUDAStream().stream();
    const dim3 threads(32,4,1);
    const uint64_t maxGridY = at::cuda::getCurrentDeviceProperties()->maxGridSize[1];
    const dim3 blocks(1, std::min((uint64_t)n1, maxGridY), 1);
    // 这段代码计算内核函数需要多少共享内存。如果threads.y大于1，它会根据U类型的大小分配足够的内存。
    int nshared =
        threads.y > 1 ?
            threads.y*sizeof(U)+(threads.y/2)*sizeof(U) :
            0;
    // 最后，函数使用cuApplyLayerNorm kernel来执行实际的LayerNorm操作。
    // kernel函数的调用使用了之前计算的线程块和线程配置，以及共享内存大小和CUDA流。
    cuApplyLayerNorm<<<blocks, threads, nshared, stream>>>(
      output, mean, invvar, input, n1, n2, U(epsilon), gamma, beta);
}

这段代码包含了kernel的启动逻辑，包括设置block的个数以及每个block中的线程排布方式，然后在cuApplyLayerNorm_里面有一个跨线程网格的大循环作用在n1维度，每个线程可能会处理多行数据。而在每一行数据的处理上，调用了cuWelfordMuSigma2 函数计算给定索引 i1 处的均值（mu）和方差（sigma2），并随后在n2维度上来计算LayerNorm的输出，同时会在每个Block的线程（0, 0）更新cuWelfordMuSigma2算出来的均值和方差（这里的记录的实际上是方差的逆）。

0x1.3 kernel实现

从上面的分析可知，整个LayerNorm实现的核心就是cuWelfordMuSigma2函数，下面对这个函数进行解析。

// `cuWelfordMuSigma2` 是一个CUDA设备函数，旨在高效计算张量某一特定维度上的均值（mu）和方差（sigma2）。
// 它基于Welford算法实现，以提高数值稳定性。此外，该函数支持仅计算均方根（RMS）作为一种操作模式。
// 模板参数 <typename T, typename U>: 定义了处理张量值（T）和执行计算（U）时使用的数据类型。
// const T* __restrict__ vals: 指向张量数据的指针。
// const int n1, n2: 指定张量的维度，其中n1是参与计算的维度的大小，n2是被约减的维度的大小。
// const int i1: 当前正在处理的n1维度上的特定索引。
// U& mu, sigma2: 用于存储计算得出的均值和方差。
// U* buf: 指向用于线程间通讯的共享内存缓冲区的指针。
// bool rms_only: 一个标志，用于指示是否仅计算RMS（为true时）或同时计算均值和方差（为false时）。
template<typename T, typename U> __device__
void cuWelfordMuSigma2(
  const T* __restrict__ vals,
  const int n1,
  const int n2,
  const int i1,
  U& mu,
  U& sigma2,
  U* buf,
  bool rms_only)
{
  // 前提条件:
  // 1) blockDim.x 等于 warp 的大小。
  // 2) 输入的张量在内存中连续存储。
  // 3) 有足够的共享内存可用，大小为 2*blockDim.y*sizeof(U) + blockDim.y*sizeof(int)。
  //
  // 在 n2 维度上计算方差和均值。
  // 初始化 count, mu, 和 sigma2 为零。
  U count = U(0);
  mu= U(0);
  sigma2 = U(0);
  // 确保处理的 i1 索引在张量的有效范围内。
  if (i1 < n1) {
    // 一个warp处理一个n1索引，同步是隐含的。
    // 用标准的Welford算法进行初始化。
    const int numx = blockDim.x * blockDim.y; // 计算一个 CUDA 块中的线程总数。
    const int thrx = threadIdx.x + threadIdx.y * blockDim.x; // 计算当前线程在块内的唯一线性索引
    // 将 lvals 指针设置为指向当前处理的 i1 索引处张量的开始位置。
    // vals 是整个张量数据的起始指针，i1*n2 计算出当前索引在张量中的线性位置。
    const T* lvals = vals + i1*n2;
    // 用局部变量l遍历张量的元素，每个线程处理多个元素。
    int l = 4*thrx;
    // 遍历张量的元素，步长为4*numx，每个线程处理四个元素。
    for (;  l+3 < n2;  l+=4*numx) {
      // 在每次外循环的迭代中，处理四个连续的元素。
      for (int k = 0;  k < 4;  ++k) {
        // 将当前处理的元素值转换为计算使用的数据类型（U）。
        U curr = static_cast<U>(lvals[l+k]);
        // 根据 rms_only 标志调用相应的函数来更新均值和方差或仅更新平方和（用于计算 RMS）。
        if (!rms_only) {
          cuWelfordOnlineSum<U>(curr,mu,sigma2,count);
        } else {
          cuRMSOnlineSum<U>(curr, sigma2);
        }
      }
    }
    // 这个循环处理了之前在步长为 4*numx 的循环中未处理的张量元素。每个线程独立处理它们剩余的部分。
    for (;  l < n2;  ++l) {
      U curr = static_cast<U>(lvals[l]);
      if (!rms_only) {
        cuWelfordOnlineSum<U>(curr,mu,sigma2,count);
      } else {
       cuRMSOnlineSum<U>(curr, sigma2);
      }
    }
    // 在同一个warp内进行归约操作。
    for (int l = 0;  l <= 4;  ++l) {
      // 是在 CUDA 设备上进行 warp 内部数据交换的关键部分。
      // 这行代码用于确定在一个 warp（32个线程）内，每个线程应该从哪个“lane”（即其他线程）获取数据。
      // （1<<l）这个操作在这里用于逐步增加要从中获取数据的线程的距离。例如，当 l 为 0 时，
      // 线程将从它的“邻居”线程（即下一个线程）获取数据；当 l 为 1 时，它将从两个位置之外的线程获取数据，依此类推。
      // 这个表达式计算出当前线程应该从哪个线程获取数据。随着 l 的增加，每个线程从越来越远的线程获取数据。
      // &31是因为在一个 warp 内，线程索引是循环的。也就是说，如果一个线程的索引计算结果是 32，
      // 它实际上会从索引为 0 的线程获取数据，索引为 33 的线程实际上是索引为 1 的线程，依此类推。
      int srcLaneB = (threadIdx.x+(1<<l))&31;
      // 是一种 warp 内部的快速数据交换操作，用于从另一个线程（srcLaneB）获取数据。
      U sigma2B = WARP_SHFL(sigma2, srcLaneB);
      // 如果不是只计算 RMS（!rms_only），则使用 cuChanOnlineSum 合并两个线程的 mu、sigma2 和 count。
      // 如果只计算 RMS，则使用 cuChanRMSOnlineSum 合并 sigma2。
      if (!rms_only) {
        U muB = WARP_SHFL(mu, srcLaneB);
        U countB = WARP_SHFL(count, srcLaneB);
        cuChanOnlineSum<U>(muB,sigma2B,countB,mu,sigma2,count);
      } else {
        cuChanRMSOnlineSum<U>(sigma2B, sigma2);
      }
    }
    // threadIdx.x == 0 has correct values for each warp
    // inter-warp reductions
    // 检查是否有多个 warp。如果 blockDim.y 大于 1，则表示块中有多个 warp 需要进行reduce操作。
    if (blockDim.y > 1) {
      // 为方差和均值的reduce操作分配共享内存。ubuf 用于存储方差和均值，ibuf 用于存储计数。
      U* ubuf = (U*)buf;
      U* ibuf = (U*)(ubuf + blockDim.y);
      // 这个循环是对 warp 间的reduce操作进行分层合并。
      for (int offset = blockDim.y/2;  offset > 0;  offset /= 2) {
        // upper half of warps write to shared
        // 确保只有部分线程（warp 的上半部分）将其计算的结果写入共享内存。
        if (threadIdx.x == 0 && threadIdx.y >= offset && threadIdx.y < 2*offset) {
          const int wrt_y = threadIdx.y - offset;
          if (!rms_only) {
            ubuf[2*wrt_y] = mu;
            ibuf[wrt_y] = count;
          }
          ubuf[2*wrt_y+1] = sigma2;
        }
        // 同步以等待共享内存存储完毕
        __syncthreads();
        // lower half merges
        // 此部分是对 warp 间数据的合并操作。
        // 确保只有部分线程（warp 的下半部分）从共享内存中读取数据并进行合并。
        if (threadIdx.x == 0 && threadIdx.y < offset) {
          U sigma2B = ubuf[2*threadIdx.y+1];
          if (!rms_only) {
            U muB = ubuf[2*threadIdx.y];
            U countB = ibuf[threadIdx.y];
            cuChanOnlineSum<U>(muB,sigma2B,countB,mu,sigma2,count);
          } else {
            cuChanRMSOnlineSum<U>(sigma2B,sigma2);
          }
        }
        __syncthreads();
      }
      // threadIdx.x = 0 && threadIdx.y == 0 only thread that has correct values
      // 最终的结果由块内的第一个线程（threadIdx.x == 0 && threadIdx.y == 0）计算并写入共享内存。
      if (threadIdx.x == 0 && threadIdx.y == 0) {
        if (!rms_only) {
          ubuf[0] = mu;
        }
        ubuf[1] = sigma2;
      }
      __syncthreads();
      // 如果不是只计算 RMS，则还需要更新均值 mu。
      if (!rms_only) {
        mu = ubuf[0];
      }
      // 计算最终的方差。
      sigma2 = ubuf[1]/U(n2);
      // don't care about final value of count, we know count == n2
    } 
    // 如果块中只有一个 warp（blockDim.y == 1），则通过 WARP_SHFL 直接在 warp 内进行数据交换和更新。
    else {
      if (!rms_only) {
        mu = WARP_SHFL(mu, 0);
      }
      sigma2 = WARP_SHFL(sigma2/U(n2), 0);
    }
  }

cuWelfordMuSigma2函数就是在n2维度上使用工具函数章节的Weleford方法来完成均值和方差的计算，然后这里还借助了共享内存来做warp内和warp间的reduce，最终得到全局的均值和方差。

前向的kernel就分析到这里，大家如果想对LayerNorm的优化做进一步的了解，推荐看一下OneFlow的SoftMax和LayerNorm优化文章。CUDA优化之LayerNorm性能优化实践(https://zhuanlan.zhihu.com/p/443026261) ，这篇文章也是讲解了LayerNorm的前向优化流程，文章开头有一张性能的图：

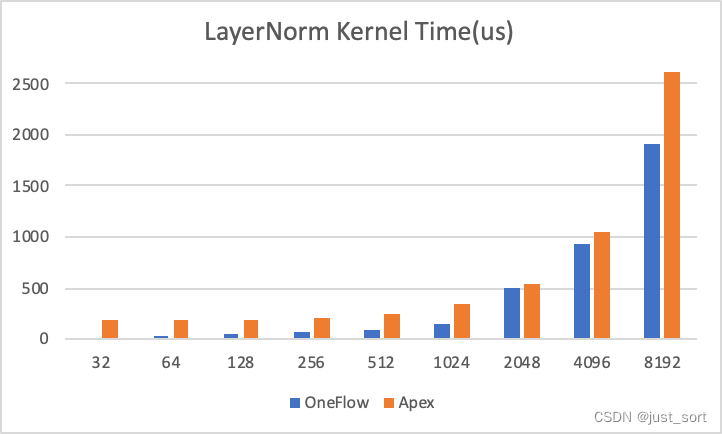
实际上在大模型时代，我们的隐藏层维度已经越来越大了，所以我们在实际训练的时候，OneFlow版本的kernel相比于apex的layerNorm在13B之类的模型训练里就拿不到明显收益了。而在CV中，由于做LayerNorm的维度可能相对小一些，所以相比于apex的LayerNorm就可以取得明显加速。

0x2. Apex的LayerNorm反向cuda实现（memory_efficient相关计算）

在apex的LayerNorm反向实现时我们不仅要关注它的cuda kernel是怎么写的，还要关注memory_efficient打开时是如何根据输出来计算梯度的。我们知道LayerNorm需要对输入，gamma，beta都计算梯度，介于篇幅原因，这里对实现得最复杂的gamma/beta的反向过程进行走读。

0x2.1 启动逻辑

这里从kernel的启动逻辑开始梳理：

// 这是一个模板函数，支持不同的数据类型：T（输入数据类型）、
// U（通常用于中间计算的数据类型，默认为float）、V（输出数据类型，默认与T相同）。
// 参数包括输出梯度（dout）、均值（mean）、方差倒数（invvar）、输入或输出的PyTorch张量（input_or_output）、
// 两个维度参数（n1、n2）、gamma和beta参数、用于数值稳定的epsilon、输入梯度（grad_input）、
// gamma梯度（grad_gamma）和beta梯度（grad_beta）、以及一个指示是否优化内存使用的布尔值（memory_efficient）。
template<typename T, typename U=float, typename V=T>
void HostLayerNormGradient(
    const V* dout,
    const U* mean,
    const U* invvar,
    at::Tensor* input_or_output,
    int n1,
    int n2,
    const V* gamma,
    const V* beta,
    double epsilon,
    T* grad_input,
    V* grad_gamma,
    V* grad_beta,
    bool memory_efficient
    )
{
    // 获取当前CUDA流以用于后续的CUDA内核调用。
    auto stream = at::cuda::getCurrentCUDAStream().stream();

    // 如果gamma和beta不为NULL，函数会计算它们的梯度。
    // 这涉及两个CUDA内核的调用：cuComputePartGradGammaBeta和cuComputeGradGammaBeta。
    if (gamma != NULL && beta != NULL) {
      // compute grad_gamma(j) and grad_beta(j)
      // part_size是分块计算梯度时的部分大小。
      const int part_size = 16;
      // threads2定义了每个CUDA线程块中的线程数量（32×4×1）。
      const dim3 threads2(32,4,1);
      // blocks2定义了CUDA网格中的块数量，其中，n2维度被分成多个块，以确保每个块可以处理n2中的一部分。
      const dim3 blocks2((n2+threads2.x-1)/threads2.x,part_size,1);
      // 这部分代码计算用于CUDA内核的共享内存大小。nshared2_a和nshared2_b是基于线程和块维度的两种不同共享内存大小估算。
      const int nshared2_a = 2 * sizeof(U) * threads2.y * threads2.y * (threads2.x + 1);
      const int nshared2_b = threads2.x * threads2.y * sizeof(U);
      // 最终选择较大的一个估算值作为实际的共享内存大小（nshared2）。
      const int nshared2 = nshared2_a > nshared2_b ? nshared2_a : nshared2_b;
      // note (mkozuki): I can hard code part_grad_gamma's dtype as float given that
      // the `cuda_layer_norm_gradient` doesn't support double.
      // 根据输入或输出张量的数据类型决定局部梯度张量part_grad_gamma和part_grad_beta的数据类型。
      // 如果输入或输出是半精度浮点数（Half）或BFloat16，则使用单精度浮点数（Float）；否则，使用输入或输出的相同数据类型。
      const auto part_grad_dtype =
        (input_or_output->scalar_type() == at::ScalarType::Half || input_or_output->scalar_type() == at::ScalarType::BFloat16) ?
        at::ScalarType::Float :
        input_or_output->scalar_type();
      // 创建两个新的PyTorch张量part_grad_gamma和part_grad_beta，用于存储gamma和beta的局部梯度计算结果。
      at::Tensor part_grad_gamma = at::empty({part_size,n2}, input_or_output->options().dtype(part_grad_dtype));
      at::Tensor part_grad_beta = at::empty_like(part_grad_gamma);
      // 使用BOOL_SWITCH宏处理memory_efficient参数，以决定是否使用内存高效版本的CUDA内核。
      // 调用cuComputePartGradGammaBeta内核计算gamma和beta的梯度。
      // 这个内核函数接收必要的输入参数，并将梯度结果写入part_grad_gamma和part_grad_beta张量。
      BOOL_SWITCH(memory_efficient, MemoryEfficient, [&]{
        auto kernel = &cuComputePartGradGammaBeta<T, U, V, MemoryEfficient>;
        kernel<<<blocks2, threads2, nshared2, stream>>>(
                        dout,
                        input_or_output->DATA_PTR<T>(),
                        n1,n2,
                        mean,
                        invvar,
                        U(epsilon),
                        gamma,
                        beta,
                        part_grad_gamma.DATA_PTR<U>(),
                        part_grad_beta.DATA_PTR<U>(),
                        epsilon,
                        false);
      });

      // 定义了每个CUDA线程块中的线程数量（32×8×1）。
      const dim3 threads3(32,8,1);
      // 定义了CUDA网格中的块数量。在这里，n2维度被分成多个块，每个块的大小由threads2.x（之前定义的线程数量）确定。
      const dim3 blocks3((n2+threads2.x-1)/threads2.x,1,1);
      // 这行代码计算了cuComputeGradGammaBeta内核所需的共享内存大小。它基于threads3线程块的维度和数据类型U的大小。
      const int nshared3 = threads3.x * threads3.y * sizeof(U);
      // kernel 接收局部梯度张量（part_grad_gamma和part_grad_beta）、块大小（part_size）、
      // 维度参数（n1和n2）和指向梯度输出的指针（grad_gamma和grad_beta）。
      cuComputeGradGammaBeta<<<blocks3, threads3, nshared3, stream>>>(
                      part_grad_gamma.DATA_PTR<U>(),
                      part_grad_beta.DATA_PTR<U>(),
                      part_size,
                      n1,n2,
                      grad_gamma,
                      grad_beta,
                      false);
    }
   ...
}

这里省略了计算输入梯度的启动代码，只看计算gamma和beta梯度的代码。可以发现，这里对gamma和beta的梯度进行计算时使用了分块计算的方式，首先会调用cuComputePartGradGammaBeta这个kernel计算出一个部分gamma和部分beta，也就是part_grad_gamma和part_grad_beta，需要注意这个kernel开启的线程块为：const dim3 blocks2((n2+threads2.x-1)/threads2.x,part_size,1)，其中part_size=16，此外每个线程块中的线程排布为：const dim3 threads2(32,4,1)，即每个线程块有128个线程。我们可以简单算一下block2的大小，threads2.x=32，那么blocks2=(n2/32,16,1)，也就是一共会有n2/2个线程块。

使用cuComputePartGradGammaBeta计算完局部gamma和beta的grad之后，会调用cuComputeGradGammaBeta这个kernel来汇总全局的gamma和beta的梯度。这里开启的线程块为：const dim3 blocks3((n2+threads2.x-1)/threads2.x,1,1)，而每个线程块里面有256个线程，排布为const dim3 threads3(32,8,1)。

现在了解了线程块的组织方式就需要去kernel实现里面对应看一下具体是怎么计算的。

0x2.2 kernel计算逻辑

首先来看分段计算gamma和beta梯度的kernel实现，注释如下：

// part_size是分块计算梯度时的部分大小。
// const int part_size = 16;
// threads2定义了每个CUDA线程块中的线程数量（32×4×1）。
// const dim3 threads2(32,4,1);
// blocks2定义了CUDA网格中的块数量，其中，n2维度被分成多个块，以确保每个块可以处理n2中的一部分。
// const dim3 blocks2((n2+threads2.x-1)/threads2.x,part_size,1);
// ->
// blockDim.x = 32, blockDim.y = 4, gridDim.y = 16
// 假设 n1 = 4, n2 = 256，并且当前是第一个线程块
template<typename T, typename U, typename V, bool MemoryEfficient> __global__
void cuComputePartGradGammaBeta(
    const V* __restrict__ dout,
    const T* __restrict__ input_or_output,
    const int n1,
    const int n2,
    const U* __restrict__ mean,
    const U* __restrict__ invvar,
    U epsilon,
    const V* __restrict__ gamma,
    const V* __restrict__ beta,
    U* part_grad_gamma,
    U* part_grad_beta,
    const double eps,
    bool rms_only)
{
    // numsegs_n1计算n1维度（4）被分成多少段。使用blockDim.y*blockDim.y（16）作为分段大小。
    // 带入值：numsegs_n1 = (4 + 16 - 1) / 16 = 1。
    const int numsegs_n1 = (n1+blockDim.y*blockDim.y-1) / (blockDim.y*blockDim.y);
    // segs_per_block计算每个线程块要处理的段数。
    // 带入值：segs_per_block = (1 + 16 - 1) / 16 = 1。
    const int segs_per_block = (numsegs_n1 + gridDim.y - 1) / gridDim.y;
    // 这些行计算当前线程块开始和结束处理n1维度的索引
    // i1_beg和i1_beg_plus_one相差segs_per_block * blockDim.y*blockDim.y=1*4*4=16
    // 带入blockIdx.y = 0：i1_beg = 0 * 1 * 4 * 4 = 0， i1_beg_plus_one = 1 * 1 * 4 * 4 = 16，i1_end = min(16, 4) = 4
    const int i1_beg = blockIdx.y * segs_per_block * blockDim.y*blockDim.y;
    const int i1_beg_plus_one = (blockIdx.y+1) * segs_per_block * blockDim.y*blockDim.y;
    const int i1_end = i1_beg_plus_one < n1 ? i1_beg_plus_one : n1;
    // row_stride用于数组访问，防止bank conflict。这里等于33
    const int row_stride = blockDim.x+1;
    // 计算每个线程在数据块中的偏移量。
    // 下限是0，上限是31。
    const int thr_load_col_off = (threadIdx.x*blockDim.y)&(blockDim.x-1);
    // 这里的下限是0，上限就是(31 * 4) / 32 + 3 * 4=15
    const int thr_load_row_off = (threadIdx.x*blockDim.y)/blockDim.x + threadIdx.y*blockDim.y;
    // i2_off是n2维度上的偏移量。
    const int i2_off = blockIdx.x * blockDim.x + thr_load_col_off;
    // 分配共享内存并设置两个缓冲区warp_buf1和warp_buf2
    SharedMemory<U> shared;
    U* buf = shared.getPointer(); // buf has at least blockDim.x * blockDim.y * blockDim.y + (blockDim.y - 1)*(blockDim.x/blockDim.y) elements
    U* warp_buf1 = (U*)buf; // 大小是 31 * 4 * 4 = 496
    U* warp_buf2 = warp_buf1 + blockDim.y * blockDim.y * row_stride; // 大小是 3 * (32 / 4) = 24
    
    // compute partial sums from strided inputs
    // do this to increase number of loads in flight
    cuLoadWriteStridedInputs<T, U, V, MemoryEfficient>(i1_beg,thr_load_row_off,thr_load_col_off,i2_off,row_stride,warp_buf1,warp_buf2,input_or_output,dout,i1_end,n2,mean,invvar,gamma,beta,eps, rms_only);
    // for循环处理每个数据块（由i1_beg和i1_end确定）。
    // 它在数据块之间以步幅blockDim.y*blockDim.y迭代，允许不同的线程块处理不同的数据区域。
    for (int i1_block = i1_beg+blockDim.y*blockDim.y;  i1_block < i1_end;  i1_block+=blockDim.y*blockDim.y) {
      cuLoadAddStridedInputs<T, U, V, MemoryEfficient>(i1_block,thr_load_row_off,thr_load_col_off,i2_off,row_stride,warp_buf1,warp_buf2,input_or_output,dout,i1_end,n2,mean,invvar,gamma,beta,eps, rms_only);
    }
    // 确保在所有线程完成其加载和处理操作之前，没有线程会继续执行后续的操作。
    __syncthreads();
    // inter-warp reductions
    // sum within each warp
    // 这部分代码执行内部归约，计算每个warp内部的部分和。
    // acc1和acc2分别用于累积来自warp_buf1和warp_buf2的值。这些缓冲区包含之前步骤计算的中间结果。
    U acc1 = U(0);
    U acc2 = U(0);
    // 内部循环对于blockDim.y内的每一行进行累加，if (!rms_only)条件检查是否需要执行特定的分支逻辑。
    // 需要特别注意，这个累加实际上是在列方向上也就是n2维度，在n2维度上一个线程负责计算blockDim.y列
    for (int k = 0;  k < blockDim.y;  ++k) {
      int row1 = threadIdx.y + k*blockDim.y;
      int idx1 = row1*row_stride + threadIdx.x;
      if (!rms_only) {
        acc1 += warp_buf1[idx1];
      }
      acc2 += warp_buf2[idx1];
    }
    // 累加的结果被写回到warp_buf1和warp_buf2中对应的位置。
    if (!rms_only) {
      warp_buf1[threadIdx.y*row_stride+threadIdx.x] = acc1;
    }
    warp_buf2[threadIdx.y*row_stride+threadIdx.x] = acc2;
    // 再次同步
    __syncthreads();
    // sum all warps
    // 这个循环是归约操作的一部分，用于在warp之间求和。
    // offset初始化为blockDim.y/2，每次迭代都减半，这是一种常用的并行归约模式。
    // 这个也是在n2维度做
    for (int offset = blockDim.y/2;  offset > 1;  offset /= 2) {
      // 在每次迭代中，只有threadIdx.y小于当前offset的线程会参与计算，这样可以避免重复的工作。
      if (threadIdx.y < offset) {
        // idx1和idx2是基于row_stride计算的索引，用于访问warp_buf1和warp_buf2。
        int row1 = threadIdx.y;
        int row2 = threadIdx.y + offset;
        int idx1 = row1*row_stride + threadIdx.x;
        int idx2 = row2*row_stride + threadIdx.x;
        // 对于rms_only模式的分支处理，只有在非rms_only模式下才更新warp_buf1。
        if (!rms_only) {
          warp_buf1[idx1] += warp_buf1[idx2];
        }
        warp_buf2[idx1] += warp_buf2[idx2];
      }
      // __syncthreads()在每次归约后同步所有线程，确保所有线程都完成了它们的部分归约工作。
      __syncthreads();
    }
    // i2是一个计算出的索引，表示当前线程在n2维度上的位置。
    int i2 = blockIdx.x * blockDim.x + threadIdx.x;
    // 如果当前线程的threadIdx.y为0且i2小于n2，则线程参与最终梯度的计算。
    if (threadIdx.y == 0 && i2 < n2) {
      int row1 = threadIdx.y;
      int row2 = threadIdx.y + 1;
      int idx1 = row1*row_stride + threadIdx.x;
      int idx2 = row2*row_stride + threadIdx.x;
      if (!rms_only) {
        part_grad_beta[blockIdx.y*n2+i2] = warp_buf1[idx1] + warp_buf1[idx2];
      }
      part_grad_gamma[blockIdx.y*n2+i2] = warp_buf2[idx1] + warp_buf2[idx2];
    }
}

在理解这段代码之前，有一个大前提，那就是这里的访问方式是n1是和blockDim.y绑定的，而n2是和blockDim.x绑定的，而且以二维矩阵的角度来看，n1是在列方向，而n2是在行的方向。然后const int row_stride = blockDim.x+1这一行是对共享内存进行padding避免Bank Conflict的，而在计算时对共享内存的访问就是按照列来访问，彻底避免bank conflict。

这也是为什么cuLoadWriteStridedInputs和cuLoadAddStridedInputs函数名中有一个Strided，这也暗示了它们的访问模式是跨stride的。剩下的部分其实和前向就比较类似了，做warp内和warp间的reduce。

另外一个值得注意的点是在cuLoadWriteStridedInputs和cuLoadAddStridedInputs计算时，会根据memory_efficient开关选择不同的计算公式，分别从输入和输出来计算出梯度，达到kernel内部重计算的目的。

// 这段代码定义了一个名为 cuLoadWriteStridedInputs 的 CUDA 设备函数模板，用于在计算LayerNorm的梯度时，
// 从输入张量中加载数据并进行必要的计算，将结果存储在 warp 缓冲区中。这个函数支持内存高效模式（MemoryEfficient）。
// 模板参数 T, U, V 代表不同的数据类型。
// bool MemoryEfficient 用于选择是否采用内存高效的方式处理数据。
// __device__ 表明这是一个 CUDA 设备函数。
// 函数参数包括各种用于LayerNorm梯度计算的数据，
// 如输入/输出张量、梯度张量 dout、均值 mean、逆方差 invvar、缩放参数 gamma、偏移参数 beta 等。
template<typename T, typename U, typename V, bool MemoryEfficient> __device__
void cuLoadWriteStridedInputs(
    const int i1_block,
    const int thr_load_row_off,
    const int thr_load_col_off,
    const int i2_off,
    const int row_stride,
    U* warp_buf1,
    U* warp_buf2,
    const T* input_or_output,
    const V* dout,
    const int i1_end,
    const int n2,
    const U* __restrict__ mean,
    const U* __restrict__ invvar,
    const V* __restrict__ gamma,
    const V* __restrict__ beta,
    const double eps,
    bool rms_only
    )
{
  // 计算 i1，表示当前处理的行索引。
  int i1 = i1_block+thr_load_row_off;
  if (i1 < i1_end) {
    for (int k = 0;  k < blockDim.y;  ++k) {
      // 计算列索引 i2 和用于加载和写入数据的索引。
      int i2 = i2_off + k;
      // load_idx 是从输入张量读取数据的索引，write_idx 是在 warp 缓冲区写入数据的索引。
      int load_idx = i1*n2+i2;
      int write_idx = thr_load_row_off*row_stride+thr_load_col_off+k;
      // 如果 i2 在有效范围内，则从输入张量加载数据，并进行必要的计算。
      if (i2<n2) {
        U c_h = static_cast<U>(input_or_output[load_idx]);
        U curr_dout = static_cast<U>(dout[load_idx]);
        // 根据 rms_only 和 MemoryEfficient 的值，使用不同的公式计算梯度，并将结果存储在 warp 缓冲区中。
        if (!rms_only) {
          warp_buf1[write_idx] = curr_dout;
          if (MemoryEfficient) {
            U curr_beta = static_cast<U>(beta[i2]);
            warp_buf2[write_idx] = curr_dout * (c_h - curr_beta) / static_cast<U>(clamp_by_magnitude(gamma[i2], eps));
          } else {
            warp_buf2[write_idx] = curr_dout * (c_h - mean[i1]) * invvar[i1];
          }
        } else {
          if (MemoryEfficient) {
            warp_buf2[write_idx] = curr_dout * (c_h) / static_cast<U>(clamp_by_magnitude(gamma[i2], eps));
          } else {
            warp_buf2[write_idx] = curr_dout * (c_h) * invvar[i1];
          }
        }
      } else {
        // 对于超出 n2 范围的索引，将相应的 warp 缓冲区位置设置为 0。
        if (!rms_only) {
          warp_buf1[write_idx] = U(0);
        }
        warp_buf2[write_idx] = U(0);
      }
    }
  } else {
    // 对于超出 n1 范围的索引，也将相应的 warp 缓冲区位置设置为 0。
    for (int k = 0;  k < blockDim.y;  ++k) {
      int write_idx = thr_load_row_off*row_stride+thr_load_col_off+k;
      if (!rms_only) {
        warp_buf1[write_idx] = U(0);
      }
      warp_buf2[write_idx] = U(0);
    }
  }
}

执行完cuComputePartGradGammaBeta这个kernel之后，它的输出part_grad_gamma和part_grad_beta分别以行为n2列为n1的内存视角保存了LayerNorm的局部均值和方差的梯度。

接下来会使用cuComputeGradGammaBeta这个kernel来计算全局的均值和方差的梯度，由于局部计算的时候分块大小是16，而每个线程负责了4行的计算，那么这里还需要累积16/4=4次，以得到当前行的所有局部梯度的和。

// blockDim.x = n2 / 32, blockDim.y = 1
// threadDim.x = 32, threadDim.y = 8
template<typename U, typename V> __global__
void cuComputeGradGammaBeta(
    const U* part_grad_gamma,
    const U* part_grad_beta,
    const int part_size,
    const int n1,
    const int n2,
    V* grad_gamma,
    V* grad_beta,
    bool rms_only)
{
    // sum partial gradients for gamma and beta
    SharedMemory<U> shared;
    U* buf = shared.getPointer();
    // 计算每个线程的全局索引i2，用于确定它在n2维度上的位置。
    int i2 = blockIdx.x * blockDim.x + threadIdx.x;
    // 如果线程索引i2小于n2的大小，该线程会参与计算。
    if (i2 < n2) {
      // each warp does sequential reductions until reduced part_size is num_warps
      // num_warp_reductions计算了每个warp需要进行的归约次数，
      // 这取决于part_size（每个块的大小）和blockDim.y（线程块的y维度大小）。
      int num_warp_reductions = part_size / blockDim.y;
      // sum_gamma和sum_beta分别用于累加gamma和beta的局部梯度。
      U sum_gamma = U(0);
      U sum_beta = U(0);
      // 这两行为每个线程设置了指向局部梯度数组的指针。这些指针根据线程的y索引和全局索引i2来确定。
      const U* part_grad_gamma_ptr = part_grad_gamma + threadIdx.y * num_warp_reductions * n2 + i2;
      const U* part_grad_beta_ptr = part_grad_beta + threadIdx.y * num_warp_reductions * n2 + i2;
      // 在这个循环中，每个线程累加它负责的局部梯度部分。
      // warp_offset变量用于遍历分配给每个线程的梯度段。
      for (int warp_offset = 0;  warp_offset < num_warp_reductions;  ++warp_offset) {
        sum_gamma += part_grad_gamma_ptr[warp_offset*n2];
        if (!rms_only) {
          sum_beta += part_grad_beta_ptr[warp_offset*n2];
        }
      }
      // inter-warp reductions
      // nbsize3计算了用于存储归约中间结果的共享内存大小。
      // 在这个LayerNorm的启动参数下，这里的blockDim.y是恒定为1的，所以实际上这个reduce不会工作
      const int nbsize3 = blockDim.x * blockDim.y / 2;
      // 外部循环减少归约参与的线程数，每次迭代减半。
      for (int offset = blockDim.y/2;  offset >= 1;  offset /= 2) {
        // top half write to shared memory
        // 在这个归约阶段，线程首先将其累加结果写入共享内存，然后从共享内存读取并继续累加。
        if (threadIdx.y >= offset && threadIdx.y < 2*offset) {
          const int write_idx = (threadIdx.y - offset) * blockDim.x + threadIdx.x;
          buf[write_idx] = sum_gamma;
          if (!rms_only) {
            buf[write_idx+nbsize3] = sum_beta;
          }
        }
        // __syncthreads()在每次迭代结束时同步所有线程，确保共享内存的一致性。
        __syncthreads();
        // bottom half sums
        if (threadIdx.y < offset) {
          const int read_idx = threadIdx.y * blockDim.x + threadIdx.x;
          sum_gamma += buf[read_idx];
          if (!rms_only) {
            sum_beta += buf[read_idx+nbsize3];
          }
        }
        __syncthreads();
      }
      // write out fully summed gradients
      // 如果线程是其warp中的第一个（threadIdx.y == 0），它负责将完全累加的梯度写入全局内存。
      if (threadIdx.y == 0) {
        grad_gamma[i2] = sum_gamma;
        if (!rms_only) {
          grad_beta[i2] = sum_beta;
        }
      }
    }
}

注意，for (int offset = blockDim.y/2; offset >= 1; offset /= 2) 这个循环包起来的代码在这里不会工作，因为这个kernel的启动设置中 blockDim.y=1。另外，我们知道输入的数据已经是写到全局内存里面的了，已经是同步之后的了，然后每个线程累积4次这个过程也是从global memory里面先读再计算最后写回全局内存，所以确实不需要再reduce了。

关于memory_efficient开关打开时的梯度计算公式，按照 https://github.com/NVIDIA/apex/pull/1715 这个pr 来看应该就是把原始的输入用重计算的输入替换之后再代入到之前的梯度计算公式中算出来的。

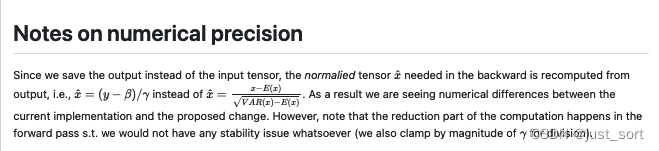
https://github.com/BBuf/how-to-optim-algorithm-in-cuda/blob/master/apex/layer_norm_cuda_kernel.cu#L579 这里就对应了对gamma的梯度，https://github.com/BBuf/how-to-optim-algorithm-in-cuda/blob/master/apex/layer_norm_cuda_kernel.cu#L582C5-L582C5 这里则对应了对beta的梯度。这里的$\hat{X}$就等于$(y?\beta )/gamma$，公式和代码实现都能完整对应上。

0x3. 总结

这篇文章记录了笔者在研究大模型训练中偶然见到的一个Trick的代码解密过程，希望对学习cuda的小伙伴有所帮助，谢谢大家。