【上分日记】第376场周赛(中位数 + 排序)

前言

?本周的力扣只写出来了两道题，都较为简单，之后的两道题个人觉得比较难想，因为我做不出来(hhh,菜鸡勿喷)。今天就来具体的总结一下。

正文

1.100161. 划分数组并满足最大差限制

• 题目链接: 100161. 划分数组并满足最大差限制

• 下面我们直接给出思路，题目如果感兴趣可以点开链接查看。

?这道题虽然做出来了，但写的的代码不太优雅，因此稍稍总结一下。

1. 我们只需排序，不断取出三个数进行比较即可。
2. 计算三个数的最大值与最小值的差。
3. 如果差小于等于k，则添加到数组中。
4. 如果差大于k，则不满足情况直接返回空即可。

• 代码：

class Solution {
public:
    vector<vector<int>> divideArray(vector<int>& nums, int k) 
    {
        vector<vector<int>> ret;
        sort(nums.begin(),nums.end());
        for(int i = 0; i < nums.size(); i += 3)
        {
            //如果最大值与最小值的差，如果大于k，直接返回空数组。
            if(nums[i + 2] - nums[i] > k)
                return vector<vector<int>>();
            //添加到数组中。
            vector<int> tmp;
            for(int j = i; j < i + 3; j++)
                tmp.push_back(nums[j]);
            ret.push_back(tmp);
        }
        return ret;
    }
};

2.100151. 使数组成为等数数组的最小代价

• 题目链接：使数组成为等数数组的最小代价

• 这道题卡了半天，还做不出来，真的寄了。

• 题目思路：

1. 准备工作，快速枚举1到10⁹ 的回文数。

如何枚举呢？我们可以这样进行思考：

1. 回文数的长度是分奇数长度和偶数长度的。
2. 奇数长度的回文数，就等于选中间的数，然后拆成两半。
3. 偶数长度的回文数，就等于直接将数砍成两半。

• 图解：
  

如何实现呢？我们可以这样进行控制进行严格递增。

• 每次枚举长度相同的数。
• 比如 1 - 9 数字长度是相同的，且为1。10, 99 长度是相同的，且为2。

如何将数字分成两种情况进行讨论呢？

• 此处我们以121进行举例：
  
• 实现代码：

vector<int> Palindromic_number;//存放回文数
//枚举函数
void enumerate()
{
	//区间左闭右开
	for (int i = 1; i < 100000; i *= 10)
	{
		for (int j = i; j < i * 10; j++)//枚举长度相同的数
		{
			int x = j;
			int t = j / 10;//枚举奇数位
			while (t)
			{
				x *= 10;
				int tmp = t % 10;
				x += tmp;
				t /= 10;
			}

			//添加到数组中
			Palindromic_number.push_back(x);
		}
		for (int j = i; j < i * 10; j++)
		{
			int x = j;
			int t = j / 10;//枚举奇数位
			while (t)
			{
				x *= 10;
				int tmp = t % 10;
				x += tmp;
				t /= 10;
			}
			//添加到数组中
			Palindromic_number.push_back(x);
		}
	}
}

2. 分析题目

• 如何做到 " 代价 " 最小 ？

• 在解题的过程中博主想到的平均数与中位数，但不知道用哪一个，下面我们来具体的分析一下。

1. 平均数(代价无法达到最小)。

下面我们来简单思考一下为什么？

先简单的举个例子：

• 平均数是用来反映整体的水平的，比如两个地区的收入。
• 可见平均数不能反应部分的情况，如果把马云的工资给各位分一分，相一个大学生也是有比较不错的收入的。

下面我们再来分析分析中位数为什么能呢？

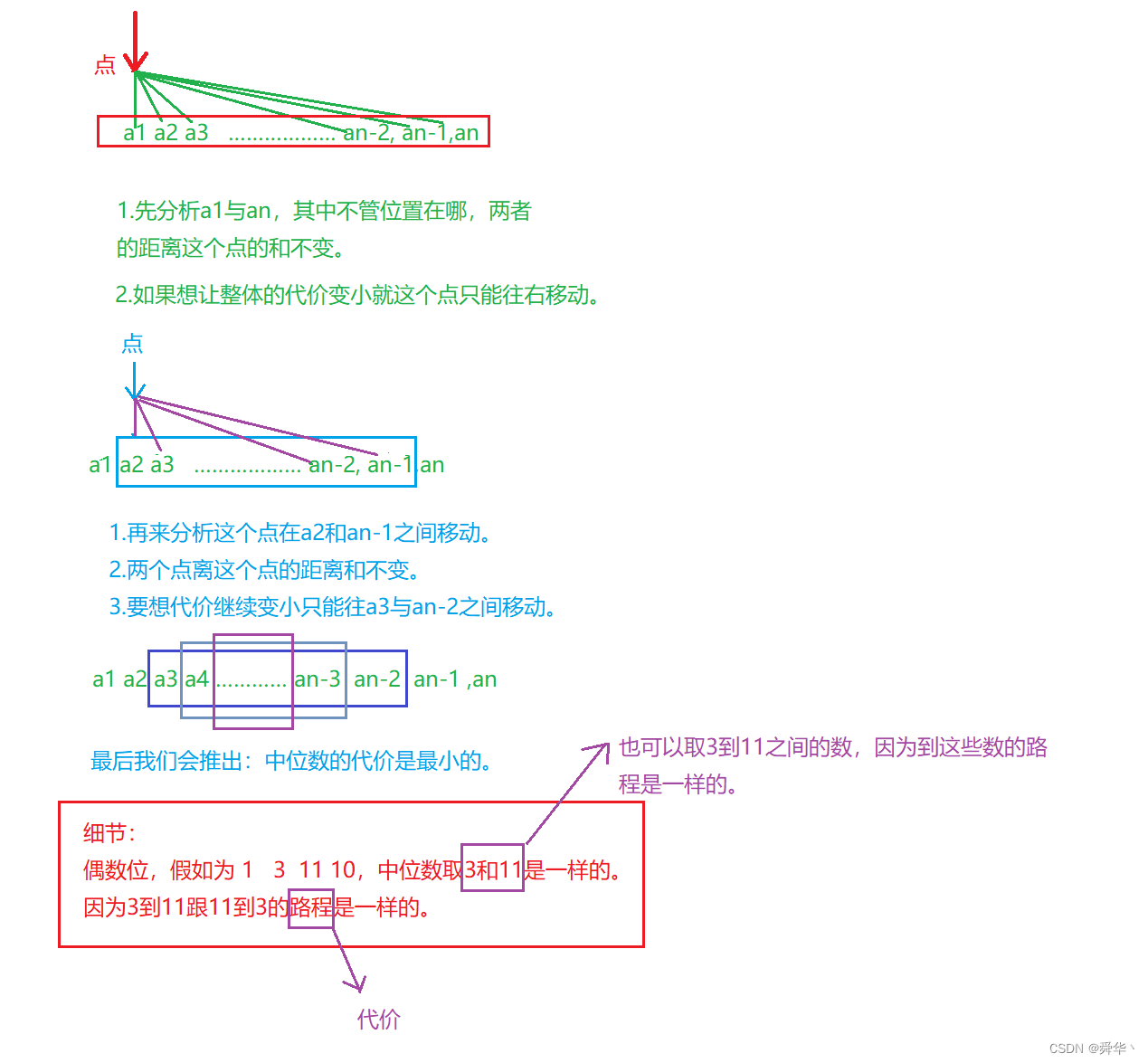
3. 结合回文数。

我们的目的就变成的，找与中位数最相近的回文数。

• 此处我们还要接着分析：

1. 如果中位数恰好为回文数，则直接计算代价即可。
2. 如果中位数不为回文数，我们要从附近的范围开始找。

• 以上默认数组以排好序。

• 实现代码：

class Solution {
public:
    vector<int> Palindromic_number;//存放回文数
    //枚举函数
    void enumerate()
    {
        //区间左闭右开
        for (int i = 1; i < 1e5; i *= 10)
        {
            for (int j = i; j < i * 10; j++)//枚举长度相同的数
            {
                int x = j;
                int t = j / 10;//枚举奇数位
                while (t)
                {
                    x *= 10;
                    int tmp = t % 10;
                    x += tmp;
                    t /= 10;
                }

                //添加到数组中
                Palindromic_number.push_back(x);
            }
            if(i < 1e4)
            {
                for (int j = i; j < i * 10; j++)
                {
                    int x = j;
                    int t = j ;//枚举偶数位
                    while (t)
                    {
                        if((long long)x * 10  > INT_MAX)
                            cout << j << endl; 
                        x *= 10;
                        int tmp = t % 10;
                        x += tmp;
                        t /= 10;
                    }
                    //添加到数组中
                    Palindromic_number.push_back(x);
                }
            }
        }
    }

    int near_palind(int num)
    {
        int index = 0;
        for(int i = 0; i < Palindromic_number.size(); i++)
        {
            if(Palindromic_number[i] >= num)
            {
                index = i;
                break;
            }
        }
        return index;
    } 
    long long cost(vector<int> &nums,int target)
    {
        long long c = 0;
        for(long long e : nums)
            c += abs((long long)target - e);
        return c;
    }
    long long minimumCost(vector<int>& nums) 
    {
        //快速枚举回文数
        enumerate();
        //添加一个数防止Palindromic_number访问越界
        Palindromic_number.push_back(1e9 + 1);
        //排序数组
        sort(nums.begin(),nums.end());
        //找离中位数最近的回文数
        int sz = nums.size();
        int left = nums[(sz - 1) / 2]; 
        int right = nums[sz / 2];
        //如果为偶数个，(sz - 1) / 2 != sz / 2;
        //如果为奇数数个，(sz - 1) / 2 == sz / 2;

        //找到第一个大于等于 left的回文数的下标.
        int index = near_palind(left);

        //先计算当前的l_cost
        long long l_cost = cost(nums,Palindromic_number[index]);
        //如果index指向的值小于等于right。
        if(Palindromic_number[index] <= right)
        {
            //说明在[left,right]之间直接返回即可
            return l_cost;
        }
        long long r_cost = cost(nums,Palindromic_number[index-1]);
		/*
		否则在Palindromic_number[index]和Palindromic_number[index-1]
		之间。
		*/
        return min(r_cost,l_cost);
    }
};

• 暴力枚举需注意——index-1可能会出现负数的情况。

3.2968. 执行操作使频率分数最大

• 题目链接：2968. 执行操作使频率分数最大

• 此题与上面的一道题的思路大致一样。
• 除此之外，多的两点是 滑动窗口 + 前缀和

1. 先来简单的解析一下。

1. 首先让每一位数都增加与减少一，限定操作次数，从而使这个数组的相同的数最多。
2. 每一位数增加或减少一 + 限定操作次数 == 所有数离某一个数距离和最近。这里的 限定操作次数 < = > 所有数据中位数的距离和。这两个数要进行比较。
3. 而且一个数组向中位数转换的操作次数是最小的。
4. 因此问题转换为是求一个子数组中，向中位数转换的距离和，目的是问这个在限定操作次数只内，这个子数组的最长的长度。

2. 具体思路。

首先我们先来讨论一下，为什么要用滑动窗口？

1. 滑动窗口使用条件：满足单调性
2. 我们再来看维护子数组的区间，right 向 右移动，这里因为新来的这个数，所有数据中位数的距离和在增加，即所需的操作次数在增加。
3. 在来看，left右移，因为要减少一个数，这个距离和就缺少了left执行的数距中位数的距离。因此所需操作次数减少。
4. 因此满足单调性，我们可以使用滑动窗口。

• 滑动窗口的使用方法，枚举右/左端点，求右/左端点。本题为枚举右端点找左端点。

1. 首先要想使子数组操作次数最小，我们先要对数组进行排序。（sort）
2. 其次我们要维护一个区间是这段区间满足的，此时向中位数转换的距离和小于等于限定次数。
3. 因此求出这段区间距中位数距离和。进行判断，如果满足则进行与当前在限定操作次数内的最长子数组求最大值。

我们还有一个点：如何快速求所有数距离中位数的和。

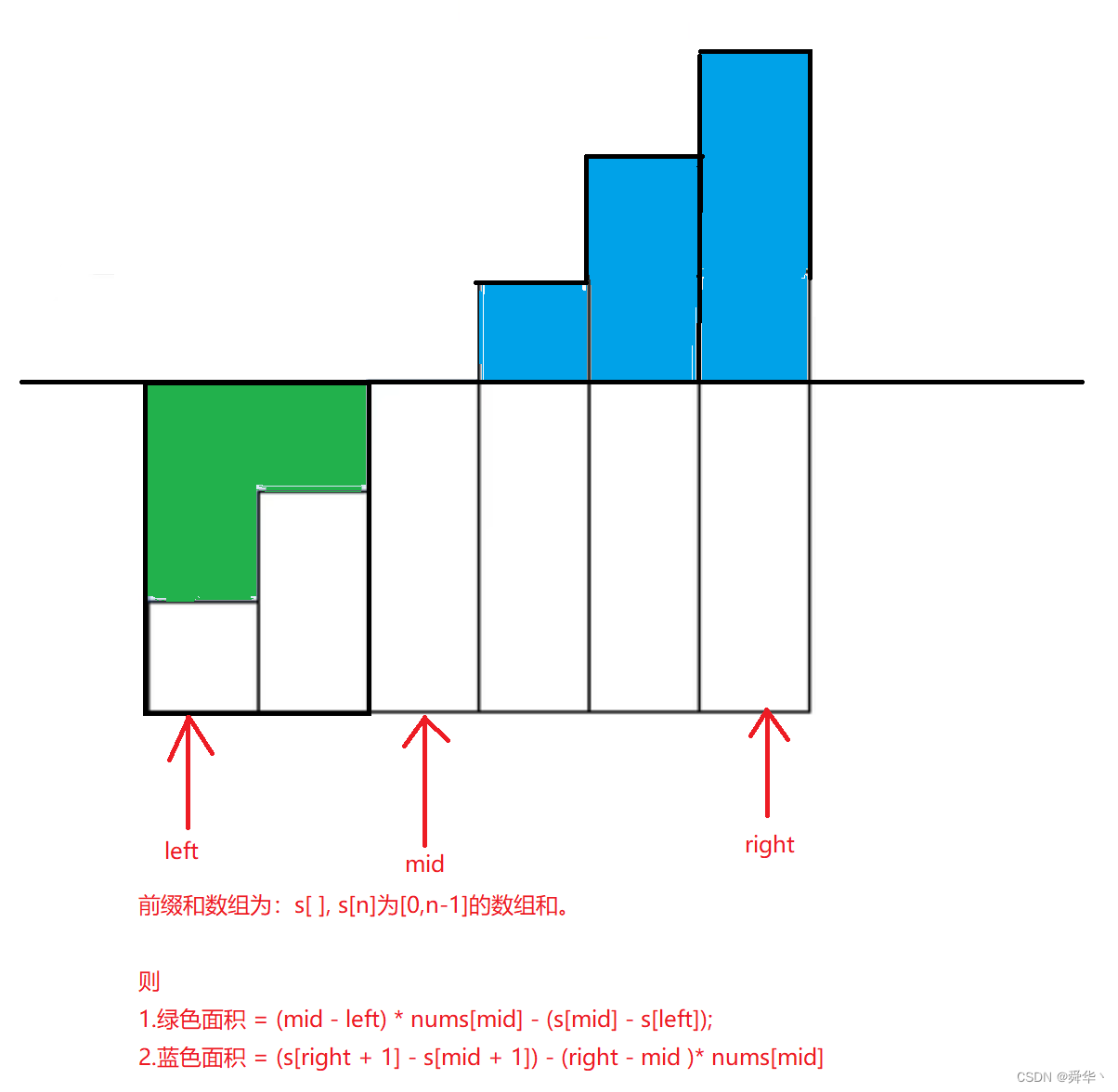
• 很明显：蓝色面积 + 绿色面积，即为距中位数的距离和。
• 细节：偶数中位数取哪一个都不影响，切入点——距离和，即代价不变，具体详见第二题。

• 实现代码：

class Solution {
public:
    int maxFrequencyScore(vector<int>& nums, long long k) 
    {
        //先进行排序
        sort(nums.begin(),nums.end());
        int sz = nums.size();

        //求前缀和
        vector<long long> s(sz + 1);
        for(int i = 1; i <= sz; i++)
            s[i] = s[i-1] + nums[i-1];
        
    
        auto distance_sum = [&](int left,int right)->long long 
        {
            int mid_i  = (left + right) / 2; 
            
            long long s_left = (long long)nums[mid_i] * \
            (mid_i - left) - (s[mid_i] - s[left]);
            
            long long s_right = (s[right+1] - s[mid_i+1]) - \
            (long long)nums[mid_i] * (right - mid_i);

            return s_left + s_right;
        };
        //滑动窗口，枚举右端点，找左端点
        int left = 0;
        int ans = 0;
        for(int right = 0; right < sz; right++)
        {
        
            while(distance_sum(left,right) > k) 
            	left++;
            	
            ans = max(ans,right - left + 1);
        }
        return ans;
    }
};

总结

• 所用算法知识：

1. 排序
2. 中位数
3. 回文数
4. 滑动窗口
5. 前缀和

?每周的周赛总结，今天就到这里了，我是舜华，期待与你的下一次相遇！