“华为杯“第十四届中国研究生数学建模竞赛-F题：地下物流系统的构建研究
发布时间：2023年12月31日
摘 要：
本文建立了地下物流节点选择聚类模型、地下物流节点选择验证模型、地下
网络设计双层优化模型、地下物流网络改进模型、地下物流网络时序与优化模型，
通过定性与定量的方法，从交通拥挤指数、一级节点转运率、节点服务覆盖率、
货运量指数、建设及运营成本、地下网络利用率、地下物流网络满意度、城市交
通需求指数进行深入的研究与探讨：
数据的搜集和处理：借助题目中已给信息和网络资源查阅的相关资料，确定
区域中心之间距离、各区域货运量以及南京市地铁的分布。
针对问题一：
在保证一级节点转运率尽量低的情况下，为实现交通拥挤指数的改善和节点
服务覆盖率尽量大的聚类目标，采用改进的
ISODATA
算法进行聚类，得到了
8
个一级节点和
22
个二级节点，并利用超效率
DEA
模型检验区域节点的效率，检
验结果和聚类得到的一二级节点结果大致相同，由此验证了一二级节点的正确性。
针对问题二：
在第一问的基础上构建了地下物流网络双层优化模型。以改善交通拥堵为上
层目标，以最小化建设及运营成本为下层目标，基于改进的粒子群算法对模型进
行求解，选择出最优的地下通道网络。通过对地下物流网络双层优化模型的求解，
得到了地下物流的规划方案，该方案的年均建设成本折旧及运营费用为
5,756,533 ,247
元。
针对问题三：
在第二问模型的基础上，基于减少建设成本、运营成本和提高地下物流网络
抗风险能力建立了地下物流网络改进模型。该模型由三个子模型构成，即地下物
流网络满意度、地下物流网络抗风险 、地下物流网络调整模型。分别采用改进
的
Dijkstra
算法、改进的粒子群算法和模拟退火算法进行模型的求解工作，经过
37
次循环后，得到改进后的地下物流网络模型，改进后的地下物流网络抗风险
指数为
6.523
，网络满意度为
6.982
，从而说明第二问的模型有改进的需要。
针对问题四：
基于动态规划理论建立了时序与动态地下物流网络优化模型，该模型以交通
拥堵情况的改善程度最大化和建造及运营成本的最小化为目标，综合考虑了城市
交通需求的增长和每年建设的线路长度基本相同的约束条件，利用动态规划的经
典求解过程对模型进行求解。结果表明，第三问的改进网络模型不再满足未来
30
年的交通需求的增长，需要进行扩容，如按照动态规划的设计思路进行设计，
将会满足城市交通需求增长，因此依据时序与动态地下物流网络优化模型进行的
动态网络建设更加符合当地实际需求。
关键词：地下物流网络、节点选择、网络满意度、交通拥挤指数、动态规划
1 问题重述
1.1 问题背景
世界大城市都遇到的一个
“
困局
”
就是交通拥堵。荷兰导航经营商
TomTom
在
2015
年发布了全球最拥堵城市排名，有十个中国大陆的城市位列前三十名。
2014
年，据中国交通部发布的数据，我国城市人口可支配收入的经济损失的
20%
是交
通拥堵带来的，相当于每年国内生产总值
(GDP)
损失
5~8%
。我国
15
座大城市的
居民每天上班相对于欧洲发达国家要多消耗
28.8
亿分钟。大量研究表明：世界
总消耗量的
20%
是由于
“
时走时停
”
的交通导致原油消耗所产生的。高峰期，北京
市主干线上拥堵
1
小时，
300
万辆机动车所需燃油为
240
万
~330
万升。
2015
年
城市交通规划年会发布数据显示：在我国石油消费方面，消费总量的
54%
是交通
石油消费，全社会总能耗
10%
以上是交通能耗，并且逐年上升。高能耗也表示着
高污染和高排放
[1-2]
。
交通需求激增所带来的地面道路上车辆、车次数量巨增是导致城市交通拥堵
的主要原因。虽然货车占城市机动车总量的比例不大，但是由于货运车辆一般体
积较大且载重时行驶较慢，如果车流中混入重型车，道路的通行能力会明显降低，
因此，占用城市道路资源比例较大。如北京，货运车辆按常规的车辆换算系数计
算
(
不同车辆在行驶时占用道路净空间的程度
)
，其占用的道路资源达
40%
。因此，
为解决城市交通和环境问题，世界各国都在进行积极探索，而处理好货运交通已
成为共识。大量实践证明，地面道路不可能无限制地增加，仅通过增加地面交通
设施来满足不断增长的交通需求，既不科学也不现实。因此
“
统筹规划地上地下
空间开发
”
势在必行，越来越多发达国家对
“
地下物流系统
”
提高重视
[3]
。
1.2 问题提出
由于我国人口众多、大城市密集、交通状况不佳已经到了迫切需要改善的程
度，而且地下工程技术水平也基本满足要求，因此构建地下物流系统已经势在必
行，而构建地下物流系统网络是其中的关键性步骤。但是目前面临着建造成本高、
网络形式多样、流量大等问题。因此为了缓解交通拥堵、降低物流成本，正确选
择地下物流网络的节点群、地下通道的网络设计和地下通道筹建是当前多国政府
正考虑和着手落实的重点领域
[4]
。
1.3 本文所要解决的问题
(1)
地下物流节点选择：根据该区域的实际情况建立该区域节点选择模型，
确定该区域地下物流网络节点群。
(2)
地下物流通道网络设计：在地下物流网络节点群的基础上选择合适的地
下路线以建立该区域的
“
地下物流系统
”
网络。在转运率变化不大的情况下，若考
虑优化网络，可适当调整一、二级节点位置。除园区至一级节点的地下通道外其
他地下通道均采用
5
吨的地下运输车辆。
(3)
网络改进：以上是分步设计网络，并未从全局出发，根据你们对地下物
流网络模型仿真结果，研究设计得到的地下物流通道网络有无修改的必要？能否
通过增加、减少节点的个数，调整节点的位置或级别，增加、减少、改变路径的
方法縮短货物运输总里程
(
同时节省运输时间
)
，降低运输成本。进一步从增强
ULS
的抗风险能力
(
如某通道中断，某方向货运量激增
)
考虑，需要对第二问的
ULS
作怎样的改动。
(4)
时序与动态优化：地下物流系统的造价高，风险大，改建困难，所以应
做好顶层设计，考虑满足该市近
30
年内的交通需求
(
可以认为需求量每年呈
5%
增长
)
并根据建设进度分八年完成
“
地下物流网络系统
”
的建设
(
每年可建设道路长
度大致相等
)
，制定南京市仙林区地下物流系统网络各线路的建设时序及演进过
程，与第三问得到的地下物流系统网络进行对比并比较优劣。
2 模型假设与符号说明
2.1 符号说明
2.2 模型假设
a.
两节点之间的距离取直线距离，认为两节点间的地质等因素不影响建设施工。
b.
南京市仙林区的地铁线路对于地下物流系统网络规划不产生影响。
c.
班车返回途中也会运载同样多的货物量。
d.
班车在两节点之间一直不间断发车，每天
18
小时，每小时
5
班次。
e.
扩容过程假设不能拆除线路只能增设线路。
f.
各节点货运量和各通道的流量的年增长率为
5%
。
3 问题分析
3.1 针对问题一
本题目的在于根据该区域实际的情况建立节点选择模型，用来确定该区域的
地下物流网络节点群。该节点群尽量满足以下的要求：交通拥堵可以得到缓解、
节点的转运率相对较小、节点覆盖面积尽量大、一二级节点的收发货量上限等。
在满足上述要求的基础之上建立合理的节点物流网络节点群。该题可以考虑成是
带约束的聚类问题，因此选择迭代自组织数据分析算
法
(
ISODATA)
。聚类的最终
结果目的是使得一级节点转运率最小、节点服务覆盖率尽量大、交通拥堵指数最
大程度上的改善。相关约束量为：一、二级节点的货运量上限、通车的地下节点
之间的距离受航班和车辆行驶速度的约束、进出
4
个物流园区的货物尽可能放入
地下运输。在满足以上约束的条件下完成对节点的选取。
.
模型校验：为了检验
上述节点分配的合理性，接下来将借助
SE-DEA
模型对其进行检验。
3.2 针对问题二
该题目是在问题一的基础之上，适当的调整一、二级节点的位置以及考虑地
下运输车辆的类型的情况下选择合适的地下线路，建立该区域的
“
地下物流系统
”
网络。该网络需要符合缓解交通拥堵和降低物流成本的要求。为此基于双层优化
建立了地下物流系统网络双层优化模型，模相关约束如下：上层为拥堵改善模块，
用来寻找改善的最优的情况，相应的约束为交通拥堵指数、地上货物运输量、地
下货物运输量。下层为物流成本优化模块，用于计算地下物流网络成本的优化，
相应的约束为地下物流线路长度、地上车辆运输货物量。双层优化的两层相互影
响和相互修正，上层决策结果一般会影响下层目标，而下层将决策结果反馈给上
层又对上层产生影响，从而实现上下层决策的相互作用。
3.3 针对问题三
从全局出发，验证上一问的结果有无修改的必要。并且在考虑抗风险的情况
下，网络作一定的调整。为了验证上述网络的合理性，建立地下物流网络改进模
型。该模型包括三个子模型：地下物流网络满意度模型、地下物流网络抗风险检
验模型和地下物流网络调整模型
地下物流网络满意度模型首先利用
Dijkstra
算法在改进模型的基础之上进行
路径优化，对改进模型进行验证。然后在考虑地下网络利用率和交通拥堵指数两
个指标基础之上，进行满意度指标的计算。
地下物流网络抗风险检验模型需要考虑一、二级节点的进、出货运量的最大
净增量和地下物流网络最大允许的中断线路条数下的抗风险指数。利用模拟退火
算法进行网络的抗风险性校验。
地下物流网络调整模型为网络优化模型，意在对网络进行满意度和抗风险能
力的优化。基于双层优化建立地下物流网络调整模型，上层为满意度优化模块，
下层为抗风险能力优化模块。改进的粒子群算法对双层优化模型进行优化改进。
3.4 针对问题四
考虑地下物流系统可以满足该区地区近
30
年的交通需求，且根据建设进度
分八年完成
“
地下物流网络系统
”
的建设时序以及演进过程。本问题是典型的动态
规划问题，考察如何在规定的时间内逐步完成网络的规划，设计的主要目标仍是
交通拥堵情况的改善程度最大化和建造及运营成本的最小化。考虑城市交通需求、
地下节点及通道内的货物每天要清仓、节点的地面收发货量上限、通车的地下节
点之间的距离受航班和车辆行驶速度的约束等因素情况下建立地下物流网络时
序与动态优化模型。利用多阶段决策过程最优化问题的动态规划算法对模型进行
求解，得到八年建设过程的建设规划。对第三问设计的地下物流网络进行城市交
通需求验证，并给出扩容方案。
4 问题一模型的建立与求解
4.1 地下物流节点选择模型的建立
该问题是一个带有约束条件的聚类问题，需要满足约束条件的前提下完成一、
二级节点的选取。
4.1.1 地下物流节点的选择指标
(1)
交通拥堵指数
(Traffic Performance Index(TPI))
交通拥堵指数是综合反映道路网畅通或拥堵的概念性数值，简称交通指数。
交通指数取值范围为
0
至
10
，每
2
个数为一等级，分别对应
“
畅通
”
、
“
基本畅通
”
、
“
轻度拥堵
”
、
“
中度拥堵
”
、
“
严重拥堵
”
五个级别，数值越高，表明交通拥堵状况
越严重。
由于该地区非人口密集区，可以近似认为区域交通的拥堵指与区域进出口之
和成正比，通过对已知数据进行拟合，得到的拟合正比例函数为：
4.1.2 地下物流节点选择模型聚类目标
4.1.3 地下物流节点选择模型约束条件
(1)
一级节点的货物量上限约束
一级节点的地面收发货量上限为 4000 吨。
4.2 节点选择聚类模型的求解
由于聚类分析算法能够挖掘数据之间的内在联系，广泛应用在数据归类处理
等问题中，相关的衍生算法应运而生。
ISODATA
算法是聚类分析衍生算法应用
较为普遍的算法之一，加入了一些试探步骤，并且可以结合成人机交互的结构，
使其能利用中间结果所取得的经验更好地进行分类。本文基于
ISODATA
算法思
想，加入一级节点聚类点的寻优约束，尽可能保证一级节点的个数最少的同时能
够有较低的一级节点转运率，对节点选择模型进行求解
[4-5]
。
4.2.1 ISODATA 算法基本步骤
ISODATA
算法的主要步骤分为以下
6
步：
(1)
选择某些初始值。可选不同的
参数指标，也可在迭代过程中人为修改，以将
N
个模式样本按指标分配到各个
聚类中心中去。
(2)
计算各类中诸样本的距离指标函数。
(3)~(5)
按给定的要求，将
前一次获得的聚类集进行分裂和合并处理
((4)
为分裂处理，
(5)
为合并处理
)
，从而
获得新的聚类中心。
(6)
重新进行迭代运算，计算各项指标，判断聚类结果是否
符合要求。经过多次迭代后，若结果收敛，则退出运算并保留结果。具体流程见
图 2。
4.2.2 改进的 ISODATA 算法求解过程
依据 ISODATA 算法流程对包含约束和目标的节点选择模型进行求解。
(14)
若是最后一次迭代运算
(
即第
100
次
)
，则算法结束；否则，根据参数的
变化决定，若需要操作者改变输入参数，转至第一步；若输入参数不变，转至第
二步。在本步运算中，迭代运算的次数每次应加
1
。
4.3 节点选择
通过上述算法进行节点
选择模型利用
matlab
编程进行求解，相关程序见附
件
2
。
4.3.1
各级节点情况
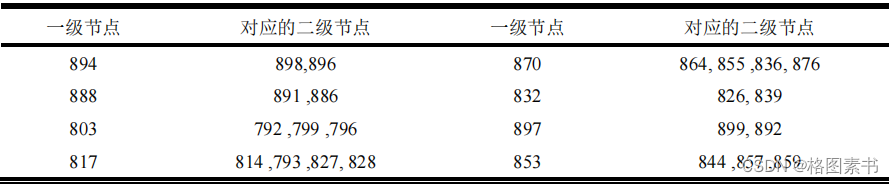
通过对节点的聚类计算，得到了
8
个一级节点和
22
个二级节点，具体节点
详见表 1。
4.3.2 节点服务范围
4.3.4 服务范围覆盖率：
4.3.4 各节点实际货运量
由于一二级节点的存在，各节点的货运量也将发生变化，一二级节点的货运
量如表
2
和表
3
所示。建设地下物流系统网络后，相当比例的货物运输是从地下
物流系统网络进行的，从而减少了货物运输对于地面交通的影响。
4.3.4 一级节点转运率
根据一级节点转运率的定义来看，仅仅需要计算从物流园区仅有最近的一级
节点转运至其他所有一级节点的货物量占物流园区总出货量的百分比，相关第一
级节点转运率如表 4 所示。
4.4 节点选择验证模型
为了检验上述节点分配的有效性，接下来将借助
SE-DEA
模型对其进行检验。
4.4.1 DEA 模型
效率性的研究大都基于各种投入产出效率模型，主要用于相同类型决策单元
4.4.2 超效率 DEA(SE-DEA)模型
在
DEA
模型的分析结果中，通常会出现多个
DMU
被评价为有效的情况。
这些有效
DMU
的效率高低无法进一步区分。
1993
年，
Anderson
和
Petersen
提
出了
“
超效率
”
模型
(Super Efficiency Model)
。超效率模型的核心就是将评价
DMU
从参考集中剔除，因此有效
DMU
的效率值一般会大于
1
，从而可以对有效
DMU
进行区分。如图
1
，在计算 C 点的效率时将其排除于参考集之外，则前沿面变为
4.4.3 模型的求解
利用超效率
DEA
模型进行各区域效率排名，以得到的
110
个区域的数据进
行分析。
投入量为： 总货运量
(
吨
)
、区域面积
(
平方米
)
产出量为： 交通拥堵指数
利用
matlab
编程求解，求解程序和结果见附件 3，效率值排序：
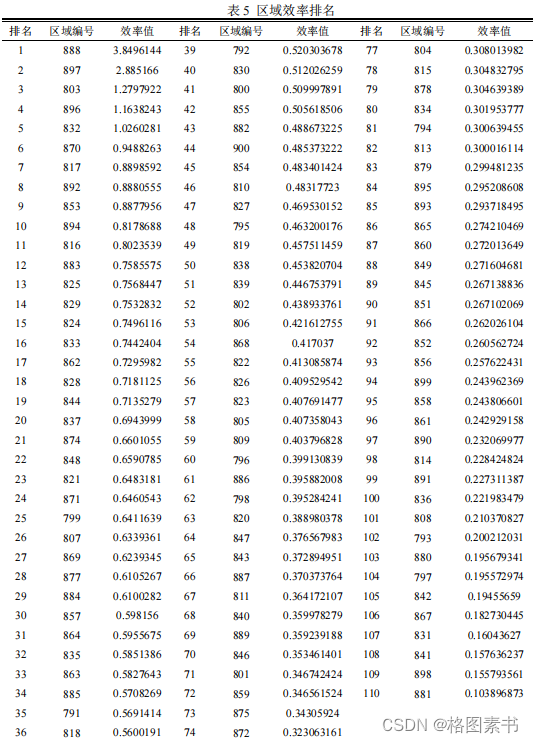
与节点选择模型计算所得结果大致相同，不过有个别节点在顺序上存在出入，
但整体上一二级节点的选择并没有偏差，间接地说明了节点选择模型的正确性。
5 问题二模型的建立与求解
5.1 地下物流网络模型
本问题为复杂网络问题，在问题一中已经确定一、二级节点的基础上，完成
地下物流网络规划工作，作为地下物流规划者来说，应从对于交通拥堵的缓解程
度和降低物流成本的角度出发选择一、二级节点的数目及位置，从而确定该区域
地下物流网络节点群。
5.1.1 地下物流网络模型的提出
地下物流系统的网络形式多样且随区域特征变化，本文总结了地下物流系统
常见的几种布局形式如表
6
所示。结合一、二级节点和布局结构的特征以及迄今
为止世界上尚未有成功经验可以借鉴，采用开发难度较小连接较多节点的树状结
构进行设计。
5.1.2 地下物流网络设计双层优化模型的建立
双层优化模型
Bracken J
和
Mc Gill J T
于
1973
年最早提出了多层规划的
概念。双层规划广泛应用在交通因素、经济调度、配电系统优化规划等领域已有
研究报道。数学上双层优化可描述为：
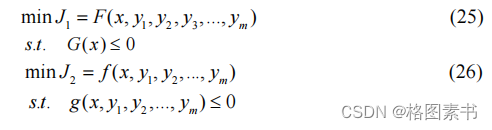
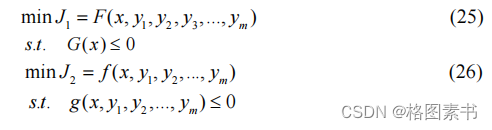
本文采用双层优化规划方法对地下物流网络选取进行优化，上层为拥堵改善
模块，用于寻找拥堵情况改善的最优程度，包括交通拥堵指数、地上货物运输量、
地下货物运输量。下层为物流成本优化模块，用于计算物流成本的优化，包括地
下物流线路长度、地上车辆运输货物量。双层优化含有两个层次，上层决策结果
一般会影响下层目标和约束条件，而下层则将决策结果反馈给上层，从而实现上下层决策的相互作用，如图 6 所示为本文双层优化逻辑图。
5.2 上层拥堵改善模型
(2)
货运量分散程度：
由于地下物流系统的造价和运营成本较高，因此应要求地下节点的货运容量
应充分被利用，即各级节点的货运量指数应尽可能大：
5.3 下层物流成本优化模型
5.3.1 目标函数
选取地下物流系统中成本优化模型为评价指标：
5.4 地下物流网络模型求解方法
基于改进粒子群的双层规划求解算法上层首先给出决策，通过控制变量的值
来引导下层，下层在上层的决策方案给定的情况下来寻找自己的最佳策略，并将
自己的最佳策略通过变量回馈给上层；为了使自己的利益最大，上层再根据下层
的反应调整自身的方案，重新做出决策，然后在上层和下层之间交互迭代，同步
优化双层规划的上层和下层，最终解得双层规划模型的近似全局最优解。本文基
于改进粒子群的双层规划求解算法的思想，在转运率变化不大的情况下，考虑优
化网络来缓解交通拥堵状况以及降低下层物流成本，适当调整一、二级节点位置，
从而选择合适的地下路线建立该地区的
“
地下物流系统
”
网络。
5.4.1 改进粒子群算法基本步骤
尽快找到全局最优解。
(9)
直到求出最优解。
gbest
和
ybest
并输出，并且求出上层模型和下层模型
对应于最优解的目标函数值。
5.5 地下物流网络模型的求解
相关求解程序见附件
4
。
5.5.1 网络构成
通过双层优化算法得到的优化网络如图
8
所示，其中粗红线表示双向四轨
（双洞）（
10
吨）、细红线表示双向双轨（双洞）（
10
吨）、粗蓝线表示双向
四轨（双洞）（
5
吨）、细蓝线表示双向双轨（双洞）（
5
吨）。
从图中可以看出，由园区至最近的一级节点的线路为双向四轨（双洞）（
10
吨）线路，说明园区对于这些一级节点的依赖较大。节点
888
和
891
以及
817
和
827
之间的线路为双向四轨（双洞）（5
吨）线路，表明在各自区域内该一二
级节点之间的关联度较强，对应的二级节点可称为
“
准一级节点”。
?
5.5.2 各节点实际货运量
由于地下物流网络的建设，各级节点均能够利用地下物流网络进行货物的转
运工作，根据结果来看，绝大部分节点地下货运量明显高于地面货运量。
5.5.3 各通道的实际流量
各通道的流量实际反映了地下物流系统网络对于交通拥挤的缓解程度。通过
表
9
可以看出大部分的通道的地下物流量高于地面流量，说明缓解交通拥挤的问
题上地下物流网络起到了至关重要的作用。
?
5.5.4 一级节点转运率变化情况
经过地下物流系统网络的设计后，一级节点的转运率均得到了一定程度的降
低，说明一级节点转运率随着网络模型的构建而降低，从另一个角度说明网络构
建的科学性。
5.5.5 地下物流网络折旧及运营成本
根据双层优化模型对网络进行优化后得到的年建造折旧及运营成本为
5,756
533,247
元。
6 问题三模型的建立与求解
6.1 地下物流网络改进模型的建立
本问题是网络优化问题，考察通过全局的角度如何进行网络节点和网络图的
优化问题，地下物流线路改进的目标是提高网络利用率和较少交通拥堵以及各环
节的费用总和最低。
6.2 地下物流网络改进指标
(1)
地下物流网络利用率
节点网络饱和度：
6.3 地下物流网络改进模型
地下物流网络的建立是为了解决地上交通拥挤问题，因此，对于地下物流网
络是否需要改进的依据是能够在满足经济性的前提下解决地上交通拥挤等问题。
将地下物流网络改进模型分为三个子模型，即地下物流网络满意度模型、地下物
流网络抗风险检验模型、地下物流网络调整模型。
6.3.1 地下物流网络满意度模型
地下物流网络满意度模型为评价模型，意在判别已知地下物流网络模型在解
决交通拥挤问题上的作用以及网络整体的利用程度的计算。
地下物流网络满意度指数
FTGW
，该指数由地下网络利用率、交通拥堵指
数改善情况两个指标构成：
6.3.2 地下物流网络抗风险检验模型
地下物流网络模型抗风险检验模型为检验模型，意在判断地下物流网络模型
的抗风险能力。
指数越大，则表示系统抗风险能力越强。
6.3.3 地下物流网络调整模型
地下物流网络调整模型为网络优化模型，意在对网络进行满意度和抗风险能
力的优化。基于双层优化建立地下物流网络调整模型，上层为满意度优化模块，
下层为抗风险能力优化模块。
(1)上层满意度调整
6.4 地下物流网络改进模型的求解
6.4.1 地下物流网络满意度模型的求解
地下物流网络满意度的求解本身并不需要对应的算法求解，但考虑需要对优
化后的地下网络进行满意度的重计算直至两者之差小于
0.1
时便输出结果，有必
要对计算满意度之前进行优化校验，即该网络是否还需优化，若仍出现路线的重
新优化，则对此次满意度计算结果进行标记，防止出现偶然因素导致满意度前后
之差小于
0.1
，导致满意度的误判。
整个算法循环只有一次，而且，如果目的点不是最后一个标记点的话，算法
循环要少于
n
次，使得时间复杂度大大降低，提高了运行效率，由于目标节点为
结束标志，因此算法准确性也得到保证。
6.4.2 地下物流网络抗风险检验模型
模拟退火算法的思想来源于对固体退火降温过程的模拟。即将固体加热至很
高温度，再让其慢慢地冷却。基于对固体退火过程的模拟，模拟退火算法用冷却
进度表来控制算法的进程，使算法在控制参数慢慢降温并趋于零时，求得组合优
化问题的相对全局最优解
[10]
。
(9)
直到求出最优解。
gbest
和
ybest
并输出，并且求出上层模型和下层模型
对应于最优解的目标函数值
[13]
。
6.4.4 三级子模型寻优过程
对于网络的优化来说，应用原始的网络数据进行满意度和抗风险验证模型的
初值设定，对于调整后的模型有必要进行优化结果校验，再进行地下物流网络满
意度的计算，因此有必要将优化验证模块归入地下网络满意度模型。
文章来源:https://blog.csdn.net/getusushu/article/details/135193309
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符，请联系我的编程经验分享网邮箱：chenni525@qq.com进行投诉反馈，一经查实，立即删除！
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符，请联系我的编程经验分享网邮箱：chenni525@qq.com进行投诉反馈，一经查实，立即删除！