SLAM算法与工程实践——SLAM基本库的安装与使用（6）：g2o优化库（2）g2o编程框架

SLAM算法与工程实践系列文章

下面是SLAM算法与工程实践系列文章的总链接，本人发表这个系列的文章链接均收录于此

SLAM算法与工程实践系列文章链接

---

下面是专栏地址：

SLAM算法与工程实践系列专栏

---

---

前言

这个系列的文章是分享SLAM相关技术算法的学习和工程实践

---

SLAM算法与工程实践——SLAM基本库的安装与使用（6）：g2o优化库（2）

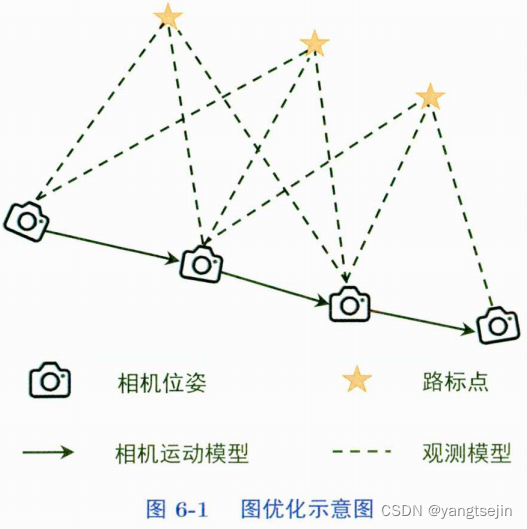
图结构：

• 顶点：待优化的变量。比如机器人位姿、空间中地图点（路标点）
• 边：顶点之间的约束产生的误差，比如重投影误差

图优化的目的是通过调整顶点来使得边的整体误差最小，此时的顶点认为是最准确的

g2o 求解曲线参数的例子

// 每个误差项优化变量维度为3，误差值维度为1
typedef g2o::BlockSolver<g2o::BlockSolverTraits<3,1>>  Block;

// 第1步：创建一个线性求解器(LinearSolver)
Block::LinearSolverType* linearSolver = new g2o::LinearSolverDense<Block::PoseMatrixType>();

// 第2步：创建块求解器(BlockSolver),并用上面定义的线性求解器初始化
Block* solver_ptr = new Block( linearSolver );

// 第3步：创建总求解器(Solver),并从GN、LM、DogLeg中选择一个，再用上述块求解器初始化
g2o::OptimizationAlgorithmLevenberg* solver = new g2o::OptimizationAlgorithmLevenberg( solver_ptr );

// 第4步：创建稀疏优化器(SparseOptimizer)
g2o::SparseOptimizer optimizer;      // 创建优化器
optimizer.setAlgorithm( solver );     // 用前面定义好的求解器作为求解方法
optimizer.setverbose( true );       // 在优化过程中输出调试信息

// 第5步：定义图的顶点，并添加到优化器中
CurveFittingVertex* v = new CurveFittingVertex();   //向图中增加顶点

v->setEstimate( Eigen::Vector3d(0,0,0) );
v->setId(0);
optimizer.addvertex( v );

// 第6步：定义图的边，并添加到优化器中
for (int i=0; i<N ; i++)    // 向图中增加边
{
    CurveFittingEdge* edge = new CurveFittingEdge(x_data[i]);
    edge->setId(i);
    edge->setvertex( 0 , v );   // 设置连接的顶点
    edge->setMeasurement(y_data[i]);     // 观测数值
    // 信息矩阵：协方差矩阵之逆
    edge->setInformation(Eigen::Matrix<double,1,1>::Identity() * 1 /(w_sigma * w_sigma));
    optimizer.addEdge( edge );
}

// 第7步：设置优化参数，开始执行优化
optimizer.initializeOptimization();
optimizer.optimize(100);    // 设置迭代次数

当然，在定义求解器变量时，可以直接一步到位，例如

// 梯度下降方法，可以从GN, LM, DogLeg 中选
auto solver = new g2o::OptimizationAlgorithmGaussNewton(g2o::make_unique<BlockSolverType>(g2o::make_unique<LinearSolverType>()));

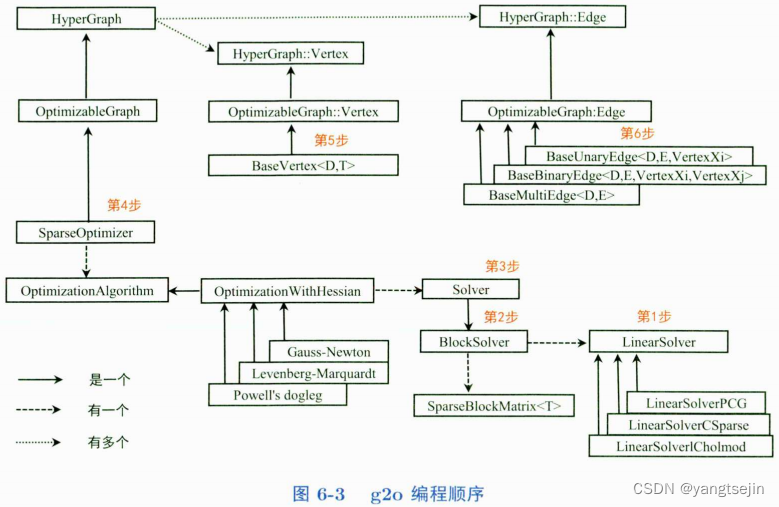
g2o求解步骤

第 1 步：创建一个线性求解器 ( LinearSolver )

我们要求的增量方程的形式是 $H\Delta x=?b$, 在通常情况下想到的方法就是直接求逆，也就是 $\Delta x=?{\mathbf{H}}^{?1}\mathbf{b}$。看起来好像很简单，但有一个前提，就是 $H$ 的维度较小，此时只需要对矩阵求逆就能解决问题。

当 $H$ 的维度较大时，矩阵求逆变得很困难，求解问题也会变得很复杂。

需要使用一些特殊的方法对矩阵进行求逆，在 g2o 中主要有以下几种线性求解方法。

LinearSolverCholmod:使用 sparse cholesky 分解法。继承自 LinearSolverCCS
LinearSolvercSparse:使用 CSparse 法。继承自 LinearSolverCCS
LinearSolverPCG:使用 preconditioned conjugate gradient 法。继承自 LinearSolver
LinearSolverDense:使用 dense cholesky 分解法。继承自 LinearSolver
LinearSolverEigen:依赖项只有 eigen,使用 eigen 中 sparse Cholesky 求解，编译好后可以在其他地方使用。继承自 LinearSolver

第2步：创建块求解器(BlockSolver)，并用上面定义的线性求解器初始化。

块求解器的内部包含线性求解器，用上面定义的线性求解器来初始化。

块求解器有两种定义方式，一种是固定变量的求解器，定义如下。

using BlockSolverPL =  BlockSolver<BlockSolverTraits<p,l>>

其中，p 表示位姿的维度，l 表示路标点的维度。另一种是可变尺寸的求解器，定义如下。

using BlockSolverX = BlockSolverPL<Eigen::Dynamic,Eigen::Dynamic>;

为何会有可变尺寸的求解器呢？

因为在某些应用场景中，位姿和路标点在程序开始时并不能被确定，此时块求解器就没办法固定变量，应该使用可变尺寸的求解器，以便让所有的参数都在中间过程中被确定。

在块求解器头文件 block_solver.h 的最后，预定义了比较常用的几种类型，这个也不用记，以后遇到了知道这些数字代表什么意思就行了

BlockSolver_6_3:表示 pose 为 6 维，观测点为 3 维。用于 3D SLAM 中的 BA
BlockSolver_7_3:在 BlockSolver_6_3 的基础上多了一个 scale
BlockSolver_3_2:表示 pose 为 3 维，观测点为 2 维

第3步：创建总求解器(Solver)，并从GN、LM、DogLeg中选择一个，再用上述块求解器初始化。

下面来看 g2o/g2o/core/ 目录，可以发现 Solver 的优化方法有3种，分别是Gauss Newton法、Levenberg-Marquardt法和Dogleg法。

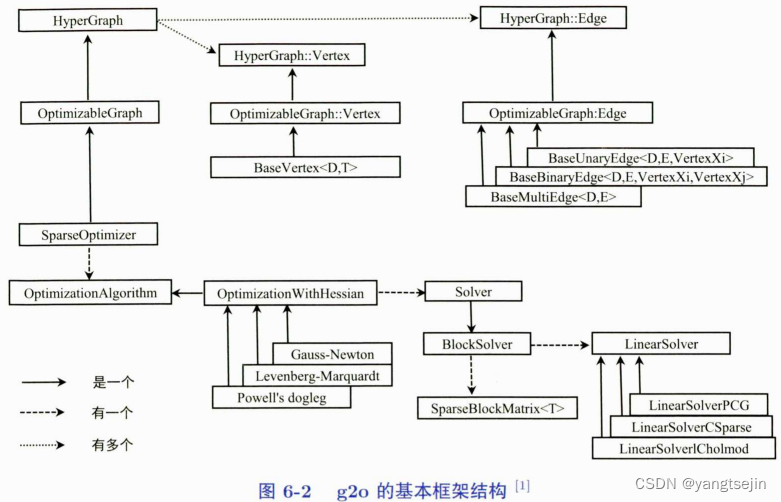
如果进入这几个算法内部，就会发现它们都继承自同一个类——OptimizationWithHessian，而 OptimizationWithHessian 又继承自OptimizationAlgorithm，和图6-2正好对应。

// optimization_algorithm gauss_newton.h
// Gauss Newton 算法
class G2O_CORE_API OptimizationAlgorithmGaussNewton : public OptimizationAlgorithmwithHessian
{
    // ......
};

// optimization_algorithm levenberg.h
// Levenberg 算法
class G2O_CORE_API OptimizationAlgorithmLevenberg : public OptimizationAlgorithmwithHessian
{
    // ......
};

// optimization algorithm dogleg.h
// Powell's Dogleg 算法
class G2O_CORE_API OptimizationAlgorithmDogleg : public OptimizationAlgorithmWithHessian
{
    // ......
};

// optimization algorithm_with_hessian.h
// brief Base for solvers operating on the approximated Hessian,e.g.,Gauss-Newton,Levenberg
class G2O_CORE_API OptimizationAlgorithmWithHessian : public OptimizationAlgorithm
{
    // ......
};

总之，在该阶段，可以选择以下3种方法，其中用得比较多的是OptimizationAlgorithmLevenberg。

g2o::OptimizationAlgorithmGaussNewton
// Gauss Newton 法
g2o::OptimizationAlgorithmLevenberg
// Levenberg-Marquardt 法
g2o::OptimizationAlgorithmDogleg
// Dogleg 法

其中用得比较多的 OptimizationAlgorithmLevenberg。

第4步，创建稀疏优化器(SparseOptimizer)，并用已定义求解器作为求解方法。

第5~6步，定义图的顶点和边，并添加到优化器中。

这部分比较复杂，我们在后面单独介绍。

第7步，设置优化参数，开始执行优化