代码随想录第三十九天(一刷&&C语言)|零钱兑换&&完全平方数
创作目的:为了方便自己后续复习重点,以及养成写博客的习惯。
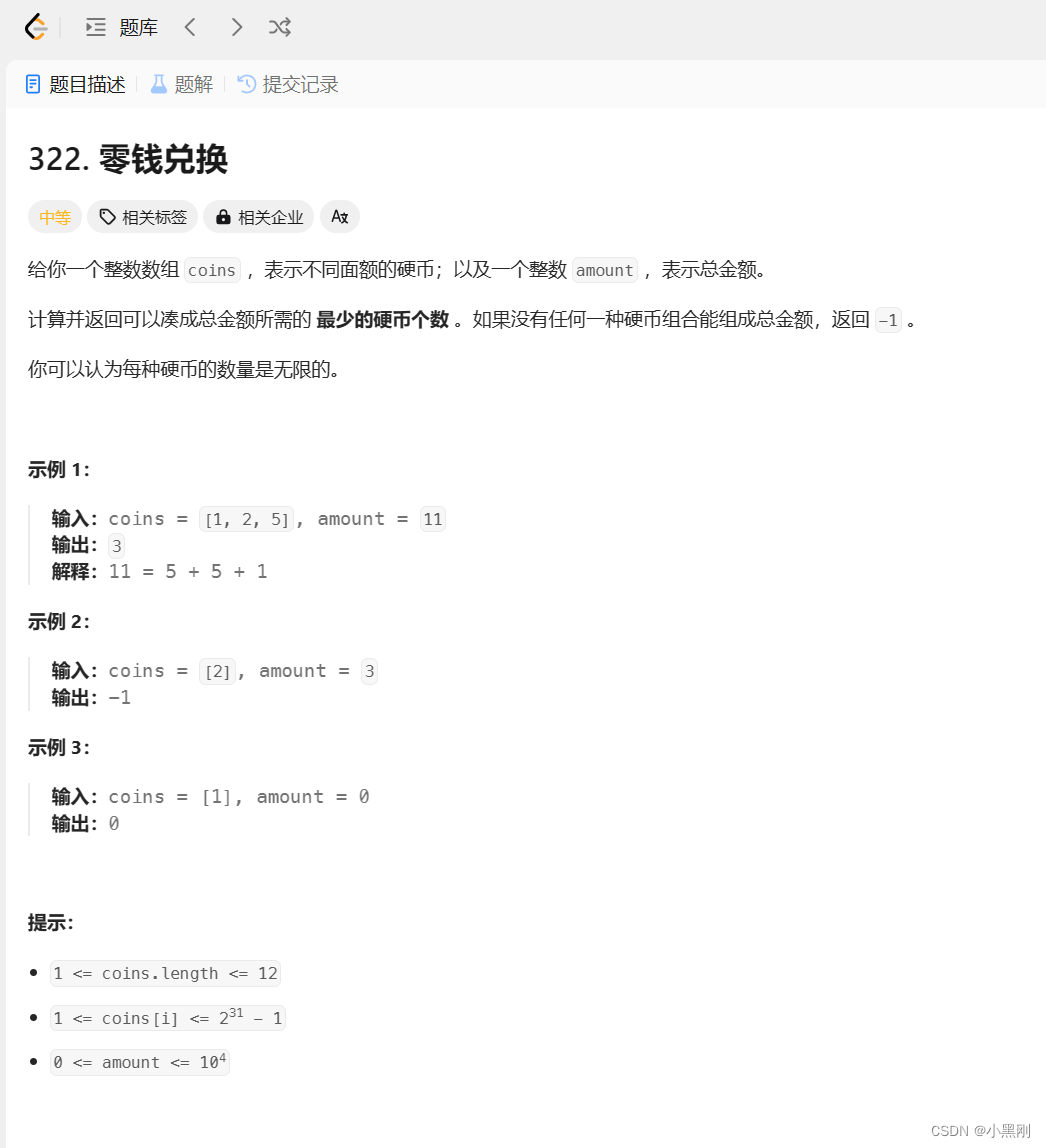
一、零钱兑换
思路:参考carl文档
1、确定dp数组以及下标的含义:凑足总额为j所需钱币的最少个数为dp[j]。
2、确定递推公式:凑足总额为j - coins[i]的最少个数为dp[j - coins[i]],那么只需要加上一个钱币coins[i]即dp[j - coins[i]] + 1就是dp[j]。dp[j] 要取所有 dp[j - coins[i]] + 1 中最小的。
递推公式:dp[j] = min(dp[j - coins[i]] + 1, dp[j])。
3、dp数组如何初始化:总金额为0所需钱币的个数一定是0,dp[0] = 0。dp[j]初始化为一个最大的数,否则在min(dp[j - coins[i]] + 1与dp[j])比较的过程中被初始值覆盖。
4、确定遍历顺序:coins(物品)放在外循环,target(背包)在内循环。且内循环正序。
5、举例推导dp数组
ledcode题目:https://leetcode.cn/problems/coin-change/description/
AC代码:
int coinChange(int* coins, int coinsSize, int amount) {
int dp[amount + 1];
dp[0] = 0;
for (int i = 1; i <= amount; i++) {
dp[i] = INT_MAX;
for (int j = 0; j < coinsSize; j++) {
if (coins[j] <= i && dp[i - coins[j]] != INT_MAX) {
if (dp[i - coins[j]] + 1 < dp[i]) {
dp[i] = dp[i - coins[j]] + 1;
}
}
}
}
return dp[amount] == INT_MAX ? -1 : dp[amount];
}三、完全平方数
思路:参考carl文档
1、确定dp数组以及下标的含义:dp[j]:和为j的完全平方数的最少数量为dp[j]。
2、确定递推公式:dp[j] 可以由dp[j - i * i]推出, dp[j - i * i] + 1 可以凑成dp[j]。选择最小的dp[j],所以递推公式为dp[j] = min(dp[j - i * i] + 1, dp[j])。
3、dp数组如何初始化:dp[0]表示和为0的完全平方数的最小数量,dp[0]=0。从递归公式dp[j] = min(dp[j - i * i] + 1, dp[j])。中可以看出每次dp[j]都要选最小的,所以非0下标的dp[j]一定要初始为最大值,这样dp[j]在递推的时候才不会被初始值覆盖。
4、确定遍历顺序:外层for循环遍历物品,内层for遍历背包。
5、举例推导dp数组
ledcode题目:https://leetcode.cn/problems/perfect-squares/description/

AC代码:
int numSquares(int n) {
int f[n + 1];
f[0] = 0;
for (int i = 1; i <= n; i++) {
int minn = INT_MAX;
for (int j = 1; j * j <= i; j++) {
minn = fmin(minn, f[i - j * j]);
}
f[i] = minn + 1;
}
return f[n];
}
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- Samtec微波、毫米波连接器系统实现卓越性能
- springboot 项目访问静态资源遇到的问题,WebMvcConfigurer和WebMvcConfigurationSupport
- go语言实现文件复制、移动(cp、mv命令)
- 官宣!Meta正在训练Llama 3,将继续开源
- 【LeetCode】每日一题 2023_12_13 字典序最小回文串(双指针,模拟)
- 不通过微软商店进行安装 UWP 软件
- (每日持续更新)信息系统项目管理(第四版)(高级项目管理)考试重点整理第4章 信息系统管理(一)
- 营销系统升级:运荔枝无代码集成电商API功能
- LearnDash LMS ProPanel在线学习系统课程创作者的分析工具
- 用python 產生 PDF檔案