【排序算法】快速排序（C语言）
【排序算法】—— 快速排序
目录
一、快速排序的单趟排序
? 快速排序的单趟排序是以一个数作为基准值，实现将数组中比基准数小的数放在基准值的左侧，比基准值大的数放在基准值的右侧。
? 我们共有3种实现方法。
1. 霍尔法
? 霍尔是最初发现快速排序的人，它使用的单趟排序算法被称为霍尔法。
? 用key标记基准值的下标(这里是数组第一个元素下标)，利用两个指针left和right分别指向待排数组的最左侧和最右侧，right指针找比key基准值小的数，left找比key基准值大的数，找到后将两个数交换位置，同时实现大数右移和小数左移，直到left与right相遇则排序完成，此时将key基准值的下标返回给函数调用者就完成了单趟排序。
left记录左下标，从左向右遍历，right记录右下标，从右向左遍历，以第一个数作为基准值key
right先出发，寻找比key小的值，若是找到则停下来
- 然后
left再出发，寻找比key大的值，若是找到则停下来，与right的值进行交换
- 接着
right寻找比key小的值，找到后left找比key大的值，直到left遇到right，此时left和right指向同一个数
- 将
left与right指向的数与key进行交换，则单趟排序就完成了，最后将基准值的下标返回给函数调用者
如何保证相遇位置比key小：因为right先走
right停下时，left与right相遇，由于right找比key小的值，所以此时right的位置一定比key小left停下时，right与left进行交换，交换后left指向的值比key小，此时right遇到left的位置一定比key小
代码实现
int PartSort(int* arr, int left, int right)
{
int key = left; //使用key保存基准值下标
while (left < right)
{
while (left < right && arr[key] <= arr[right]) //只找小的，等于要过滤，找前判断right有没有走过
{
right--;
}
while (left < right && arr[key] >= arr[left])
{
left++;
}
if (left < right) //没有相遇时左右交换
{
Swap(&arr[left], &arr[right]);
}
}
Swap(&arr[key], &arr[left]); //交换基准值和相遇位置的值，并返回基准值的下标
return left;
}
2. 挖坑法
? 挖坑法是将key基准值用变量单独保存，然后将key的位置空出来形成一个坑，left和right指针分别从左右两端向中心遍历，此时left先指向这个坑，right找比key小的数，找到后将该数直接放进坑里，并将自己空出来的位置设置为坑，left找比key大的数，找到后将该数放进坑里，并将现在空出来的位置设置为坑，一直遍历，直到left与right相遇，相遇位置一定为坑(left和right必定有一个指向坑)，此时将key基准值放进坑内，并返回基准值下标完成单趟排序
- 先定义变量
key，存储数组第一个数作为key，此时left指向的位置就是坑
right开始找小，找到后停止，将right位置的数放进坑里，此时right位置作为新的坑
left继续行动，找到比key大的数停止，并将值放进坑里，此时left位置作为新坑
right接着找，依次循环，直到left与right相遇
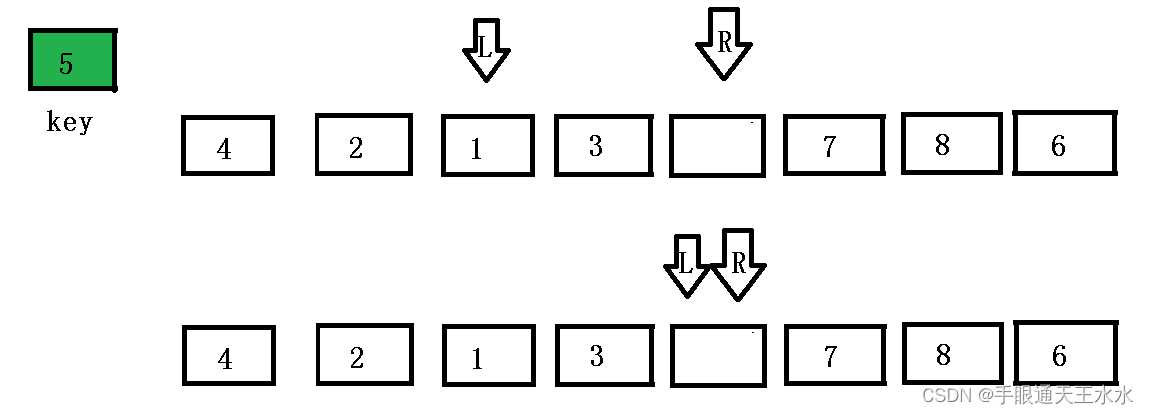
- 将
key放入相遇时的坑里，排序完毕，将key值下标返回
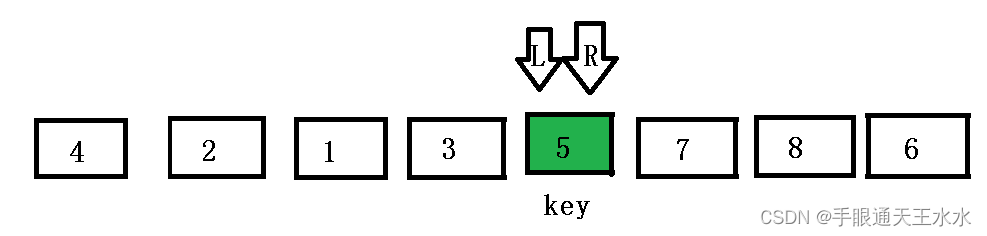
代码实现
int PartSort(int* arr, int left, int right)
{
int key = arr[left];
int hole = left;
while (left < right)
{
while (left < right && arr[right] >= key)
{
right--;
}
arr[hole] = arr[right];
hole = right;
while (left < right && arr[left] <= key)
{
left++;
}
arr[hole] = arr[left];
hole = left;
}
arr[hole] = key;
return hole;
}
3. 前后指针
? 将数组第一个元素作为key基准值，定义前指针prev指向第一个数，后指针cur指向第二个数，由cur挨个遍历数组中的数据，cur寻找比key基准值小的数，prev在cur找到小的数时才加一，并与cur位置交换数值，保证数组中较小的数在prev指针之前，而cur找到大的数时接着往前走，prev依然守着较小的数的末尾，依次类推直到cur完全遍历完数组，所以利用如此机制保证prev之前的值一定小于key基准值，而prev与cur之间的一定大于基准值(小的都被交换到prev处了)，最后将prev(小于基准值)处与key位置的数据交换，将基准值下标返回则完成单趟排序
- 开始时
prev指向第一个数，cur指向prev的下一位，此时cur位置的数比key基准值小，所以prev加一后与cur位置的数交换，由于此时prev+1 == cur，所以交换后没有变化
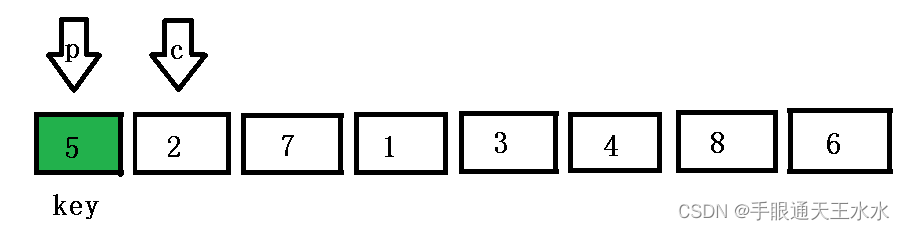
cur找到比key大的数，此时cur接着遍历，prev坚守本地
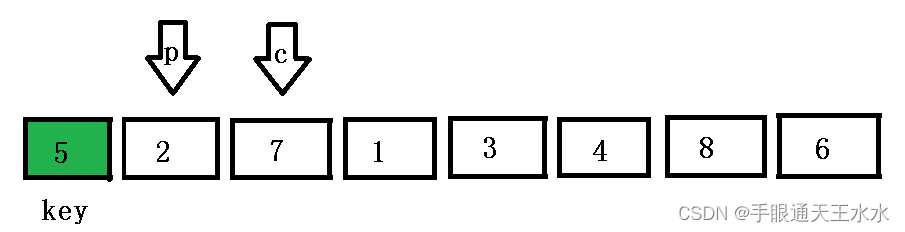
cur再次找到小的后，将prev右移一位，并与cur交换位置
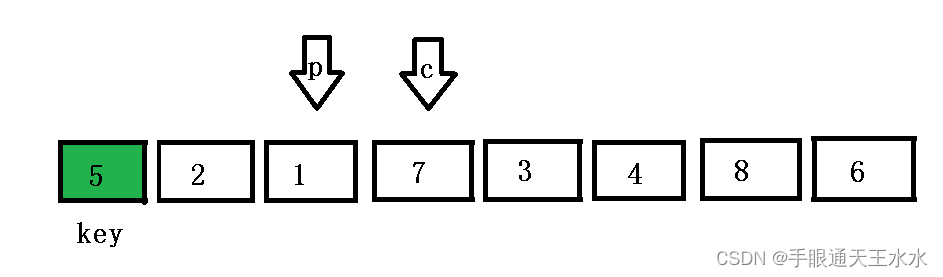
- 重复上述动作，直到遍历完整个数组
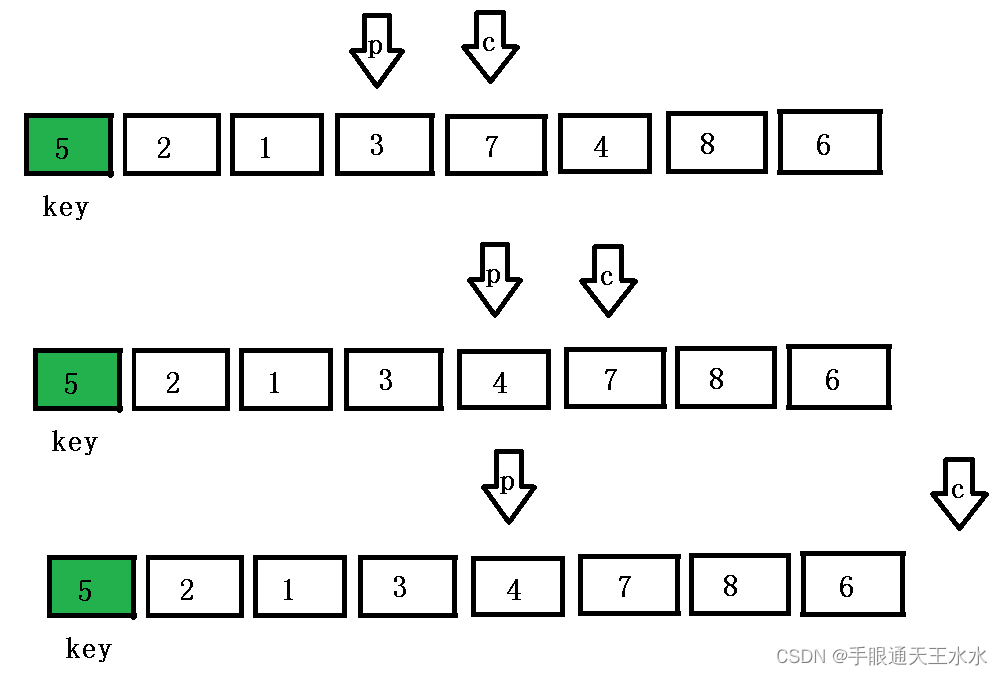
cur遍历完数组后，将prev与key交换数值，完成排序，并将key下标返回
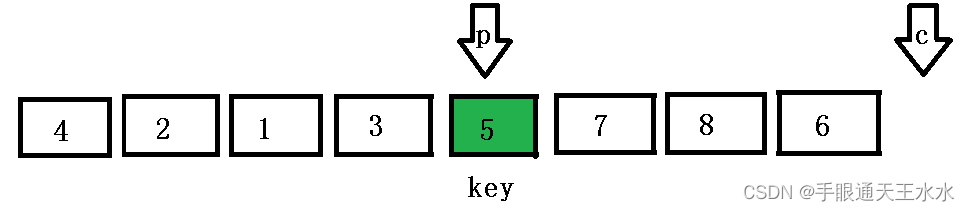
代码实现
int PartSort(int* arr, int left, int right)
{
int key = left;
int prev = left;
int cur = left + 1;
while (cur <= right)
{
//arr[cur]小于基准值就交换
if (arr[cur] <= arr[key] && ++prev != cur) //这里做了优化：如果prev+1等于cur则不用交换，该语句顺便将prev加一
{
Swap(&arr[cur], &arr[prev]);
}
cur++;
}
Swap(&arr[key], &arr[prev]);
return prev;
}
二、快速排序
? 快速排序是以一个数为基准，将数组分为两个子序列，左子序列放比基准数小的，右子序列放比基准数大的数，然后再将子序列以以上方式同样分割，直到数组有序
1. 排序步骤
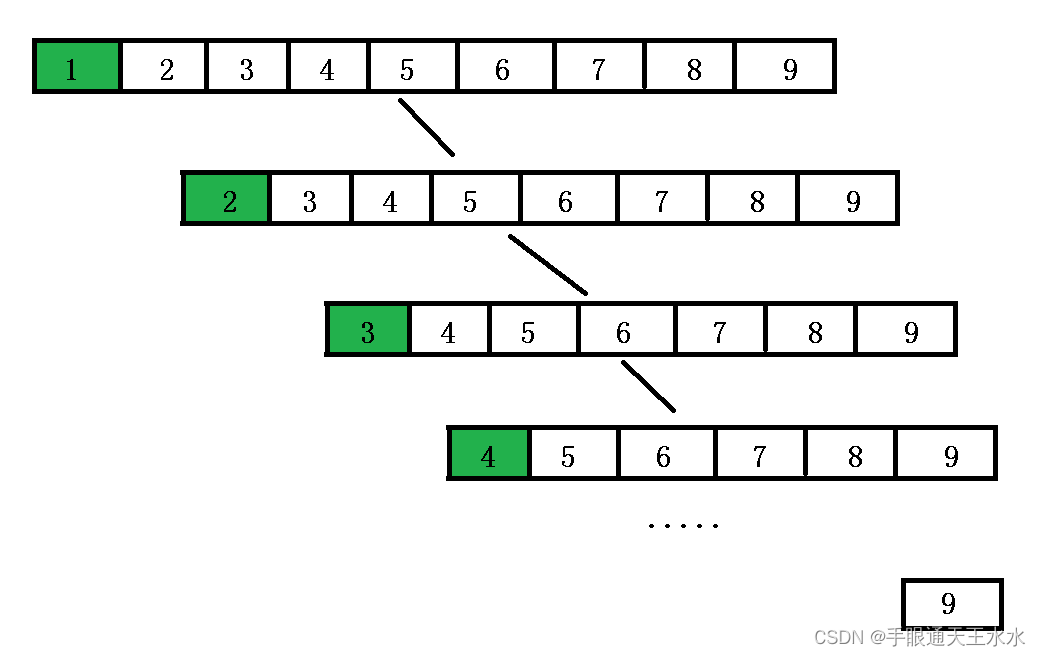
- 将下列数组以6为基准，将比6小的数放在数组右侧，比6大的数放在数组左侧，得到如下数组
- 以6为分界线，将6以前的数据作为一个数组，以3为分界线，将比3小的数放在数组左边，比3大的数放在数组右边
- 以6为分界线，将6以后的数据作为一个数组，以7为分界线，将比7小的数放在数组左边，比7大的数放在数组右边
- 再继续重复上述操作，数组就排好顺序了
2. 排序完整步骤图
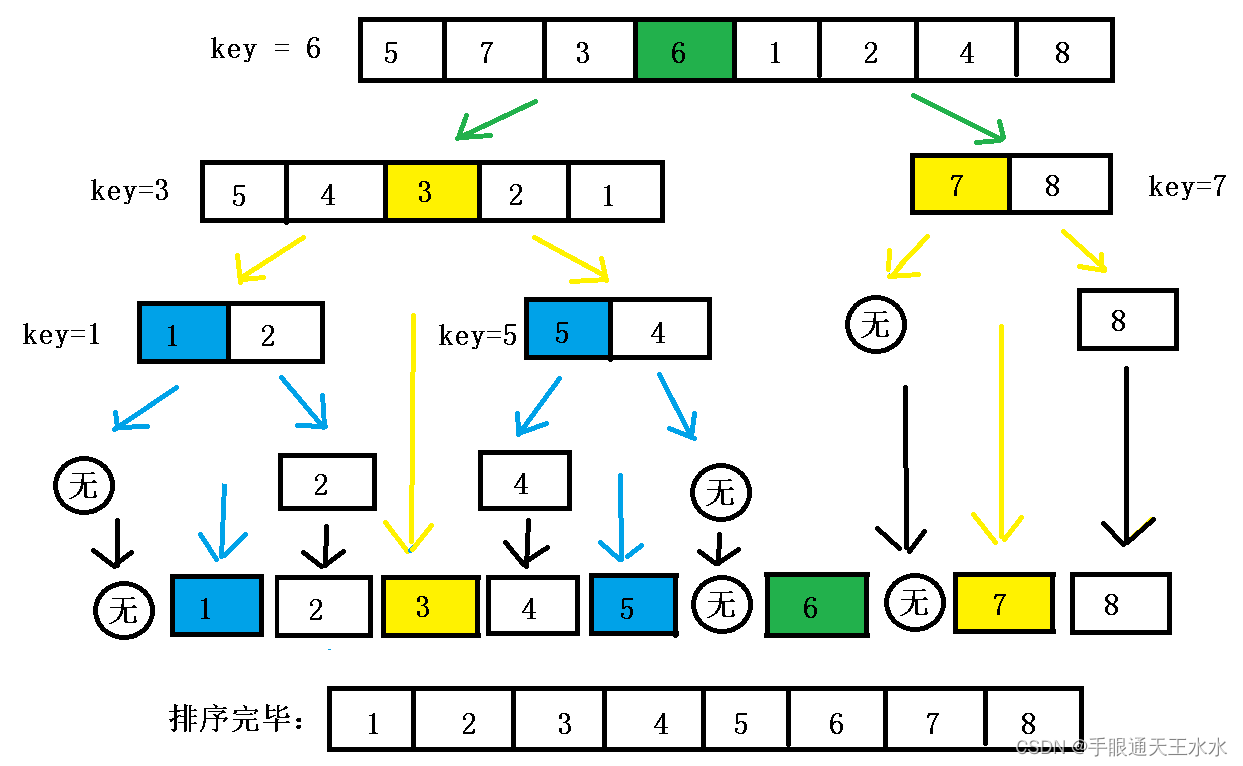
3. 快速排序代码
3.1 递归实现
? 快速排序使用递归的方式调用单趟排序，每次调用后都以基准值为界，将数组分为2个子序列，继续排序
void QuickSort(int* arr, int begin, int end)
{
if (begin >= end)
{
return;
}
int key = PartSort(arr, begin, end); //单趟排序并获取基准值
QuickSort(arr, begin, key-1); //排左序列
QuickSort(arr, key+1, end); //排右序列
}
3.2 非递归实现
? 非递归要使用栈存储每一次分割后的数组下标区间，以数组下标区间传入单趟排序实现对递归思想的模拟，具体步骤看注释
? 注意：栈的顺序是先进后出，获取区间以先右后左顺序时，就要以先左再右压栈
//栈的接口
void StackInit(Stack** pps); //初始化
void StackDestroy(Stack** pps); //销毁
void StackPush(Stack* ps, STDataType x); //入栈
void StackPop(Stack* ps); //出栈
STDataType StackTop(Stack* ps); //获取栈顶元素
_Bool StackEmpty(Stack* ps); //判空
void QuickSort(int* arr, int begin, int end)
{
//创建栈并压入数组区间
Stack *ps = NULL;
StackInit(&ps);
StackPush(ps, begin);
StackPush(ps, end);
while (!StackEmpty(ps))
{
//从栈中获取左右区间
int right = StackTop(ps);
StackPop(ps);
int left = StackTop(ps);
StackPop(ps);
//判断左右区间是否合理，若不合理则跳过本次循环
if (left >= right)
{
continue;
}
//执行单趟排序并获取基准值下标
int key = PartSort(arr, left, right);
//将基准值分割的两个区间压入栈中
StackPush(ps, left);
StackPush(ps, key-1);
StackPush(ps, key+1);
StackPush(ps, right);
}
StackDestroy(&ps);
}
三、选择基准数key
1. 为什么要选择基准数key
? 在我们选择基准值时，都是以数组中第一个数作为基准值进行排序，这样写的好处是非常方便且易懂，但是也有个大问题。
? 如果基准值是数组中最大或最小的数值，则快速排序的递归深度会非常深，排序效率会很低。若是一个有序数组使用快速排序，则递归深度为n，单趟排序也为n，时间复杂度为 O ( n 2 ) O(n^2) O(n2)
基准数的选择有3种方法：
2. 随机选一个
? 在数组中随机选择一个数作为基数，每次都选到最大或最小的概率很小，但是有概率会选到最大或最小值
#include <stdlib.h>
#include <time.h>
int GetRandIndex(int* arr, int left, int right)
{
srand((size_t)time(NULL)); //初始化随机种子
return rand() % (right-left+1) +left;
}
3. 选中间位置
? 选取左右下标的中间下标为基准值，针对有序数组能达到最大效率，但是无序数组仍可能选到最大或最小值
int GetMidIndex(int* arr, int left, int right)
{
return (left + right) / 2;
}
4. 三值取中
? 在left、right、和中间下标的值中选取一个折中值，基准值不可能为最大值或最小值
int GetMidIndex(int* arr, int left, int right)
{
int mid = (left + right) / 2;
if (arr[left] < arr[right])
{
if (arr[mid] < arr[left])
{
return left;
}
else if (arr[mid] <arr[right])
{
return mid;
}
else
{
return right;
}
}
else
{
if (arr[mid] < arr[right])
{
return right;
}
else if (arr[mid] < arr[left])
{
return mid;
}
else
{
return left;
}
}
}
? 注意：在我们选择好基准值后，为了保证原来的单趟排序保持原有状态，我们会将选好的基准数与数组中第一个数交换位置，然后使用第一个数作为基准值排序
int PartSort(int* arr, int left, int right)
{
//获取基准值，并与left交换位置
int key = GetMidIndex(arr, left, right);
Swap(&arr[key], &arr[left]);
key = left;
//单趟排序算法
...
}
四、完整代码
1. 快速排序的完整代码
? 这里是三值取中选择的基准值，挖坑法实现的单趟排序，和递归实现的快速排序，如果想使用其他方法，请自由组合（单趟排序之前别忘记交换基准数与第一个数的值）
//交换变量
void Swap(int* a, int* b)
{
int temp = *a;
*a = *b;
*b = temp;
}
//三值取中
int GetMidIndex(int* arr, int left, int right)
{
int mid = (left + right) / 2;
if (arr[left] < arr[right])
{
if (arr[mid] < arr[left])
{
return left;
}
else if (arr[mid] <arr[right])
{
return mid;
}
else
{
return right;
}
}
else
{
if (arr[mid] < arr[right])
{
return right;
}
else if (arr[mid] < arr[left])
{
return mid;
}
else
{
return left;
}
}
}
//挖坑法单趟排序
int PartSort(int* arr, int left, int right)
{
//获取基准值，并与left交换位置
int key = GetMidIndex(arr, left, right);
Swap(&arr[key], &arr[left]);
int key = arr[left];
int hole = left;
while (left < right)
{
while (left < right && arr[right] >= key)
{
right--;
}
arr[hole] = arr[right];
hole = right;
while (left < right && arr[left] <= key)
{
left++;
}
arr[hole] = arr[left];
hole = left;
}
arr[hole] = key;
return hole;
}
//快速排序递归实现
void QuickSort(int* arr, int begin, int end)
{
if (begin >= end)
{
return;
}
int key = PartSort(arr, begin, end); //单趟排序并获取基准值
QuickSort(arr, begin, key-1); //排左序列
QuickSort(arr, key+1, end); //排右序列
}
2. 快速排序的优化
? 快速排序时以递归形式（非递归也是用栈模拟递归方法）对分好大小的两个子序列进行单趟排序，若是递归到较深处时，待排数组较短，此时再使用递归方式对短数组进行快速排序就会导致效率下降，所以优化的方式就是设置一个数组排序的长度下限，若是数组长度到达下限以下，则不再调用快速排序，而是调用插入排序。
? 为什么快速排序递归到深处时效率会下降
快速排序的递归类似于二叉树的形式，深度越深待排数组的长度越短，但是数量也越多，调用函数的次数就越多，开辟函数栈帧的消耗越大，导致效率下降
? 为什么待排数组较短时调用的是插入排序
- 冒泡排序、选择排序、插入排序的时间复杂度都是 O ( n 2 ) O(n^2) O(n2)
- 冒泡排序每一次单趟排序都会执行
n-1次，一共执行n-1次单趟排序，若是做出优化，单趟排序已经有序，则停止执行- 选择排序每一次单趟排序都会执行
n次，一共执行n/2次单趟排序，无论数组是否有序执行次数都不变- 插入排序每一次单趟排序都只向前遍历到最大值之后，一共执行
n次，若数组有序，则总共只执行n次，最差情况下每次都只是从i遍历到0下标，综合考虑是执行次数最优的- 希尔排序的时间复杂度是 O ( n l o g 2 n ) O(nlog_2n) O(nlog2?n)，但是对于越大的数组效率越高，数组越小效率越接近 O ( n 2 ) O(n^2) O(n2)
- 堆排序的时间复杂度也是 O ( n l o g 2 n ) O(nlog_2n) O(nlog2?n)，但是在数量很多且长度很短的数组下，建大量的堆显然不会让效率高出多少
- 桶排序（基数排序）和归并排序暂时不考虑，我还没学
//快速排序递归的优化实现
void QuickSort(int* arr, int begin, int end)
{
if (begin >= end)
{
return;
}
//数组长度小于等于8时，调用插入排序
if (end-begin+1 <= 8)
{
InsertSort(arr, end-begin+1);
return;
}
int key = PartSort(arr, begin, end); //单趟排序并获取基准值
QuickSort(arr, begin, key-1); //排左序列
QuickSort(arr, key+1, end); //排右序列
}
? 需要优化后的完整代码将以上代码直接替换前面的快速排序代码，并将插入排序代码复制到快速排序代码之前
//插入排序
void InsertSort(int* arr, int size)
{
int end = 0;
int i = 0;
for (i = 0; i < size-1; i++)
{
end = i;
int temp = arr[end + 1];
while (end >= 0)
{
if (temp < arr[end])
{
arr[end + 1] = arr[end];
end--;
}
else
{
break;
}
}
arr[end + 1] = temp;
}
}
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符，请联系我的编程经验分享网邮箱：chenni525@qq.com进行投诉反馈，一经查实，立即删除！
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码（1）
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- Linuk使用nfs建立共享目录
- 解析数据库联结：应用与实践中的 INNER JOIN、LEFT JOIN、RIGHT JOIN、FULL OUTER JOIN 与 CROSS JOIN
- 我劝你不要去体检
- [足式机器人]Part2 Dr. CAN学习笔记 - Ch03 傅里叶级数与变换
- 每天一个vue知识点
- Spring Cloud Gateway 路由配置策略
- 计算机硬件 4.5打印机扫描仪数码相机
- 【AI】人工智能爆发推进器之生成对抗网络
- 新开微信公众号何时能恢复留言功能？
- 流程挖掘在优化核心业务、增强可见性和提升自动化方面的三重效应